Baccalauréat S Antilles-Guyane 19 juin 2014 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

1. Le service sanitaire prélève une huître au hasard dans la production de l'ostréiculteur. On suppose que toutes les huitres ont la même chance d'être choisies.
On considère les évènements suivants :
• $J$ : «  l'huître prélevée est une huître japonaise » ,
• $C$ : «  l'huître prélevée est de calibre n° 3 » .
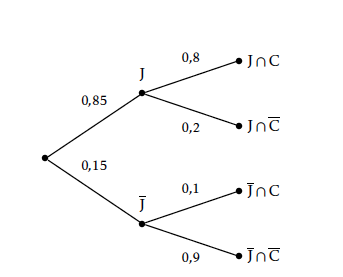
1. Construire un arbre pondéré complet traduisant la situation.

2. Calculer la probabilité que l'huître prélevée soit une huître plate de calibre n° 3.
On cherche donc $P\left( \bar{J} \cap C \right) = 0,15 \times 0,1 = 0,015$
3. Justifier que la probabilité d'obtenir une huître de calibre n° 3 est $0,695$.
D’après la propriété des probabilités totales :
$$\begin{array} \\P(C) &= P(J \cap C) + P\left( \bar{J} \cap C \right) \\
&=0,85 \times 0,8 + 0,015 \\
&= 0,695
\end{array}$$

4. Le service sanitaire a prélevé une huître de calibre n° 3. Quelle est la probabilité que ce soit une huître plate ?
On cherche à calculer :
$$\begin{array}\\ P_C\left( \bar{J} \right) & = \dfrac{P\left( C \cap \bar{J} \right)}{P(C)} \\ &= \dfrac{0,015}{0,695} \\ &=\dfrac{3}{139} \\ & \approx 0,0216 \end{array}$$
2. La masse d'une huître peut être modélisée par une variable aléatoire $X$ suivant la loi normale de moyenne $\mu = 90$ et d'écart-type $\sigma = 2$.
   1. Donner la probabilité que l'huître prélevée dans la production de l'ostréiculteur ait une masse comprise entre 87g et 89g.
   D’après la calculatrice $P(87 \le X \le 89) \approx 0,2417$
   
   2. Donner $P(X \geqslant 91)$.
   $P(X \ge 91) = 0,5 – P(90 \le X \le 91) \approx 0,3085$

Partie B

Cet ostréiculteur affirme que 60 %de ses huîtres ont une masse supérieure à 91 g. Un restaurateur souhaiterait lui acheter une grande quantité d'huîtres mais il voudrait, auparavant, vérifier l'affirmation de l'ostréiculteur. Le restaurateur achète auprès de cet ostréiculteur 10 douzaines d'huîtres qu'on considèrera comme un échantillon de $120$ huîtres tirées au hasard. Sa production est suffisamment importante pour qu'on l'assimile à un tirage avec remise. Il constate que $65$ de ces huîtres ont une masse supérieure à 91 g.

1. Soit $F$ la variable aléatoire qui à tout échantillon de $120$ huîtres associe la fréquence de celles qui ont une masse supérieure à 91g.
Après en avoir vérifié les conditions d'application, donner un intervalle de fluctuation asymptotique au seuil de 95 % de la variable aléatoire $F$. $n = 120 \ge 30$, $np = 120 \times 0,6 = 72 \ge 5$ et $n(1-p) = 48 \ge 5$
Par conséquent un intervalle de fluctuation asymptotique au seuil de $95\%$ est :
$$\begin{array}\\ I_{120} &= \left[0,6 - 1,96 \times \dfrac{\sqrt{0,6 \times 0,4}}{\sqrt{120}};0,6 + 1,96 \times \dfrac{\sqrt{0,6 \times 0,4}}{\sqrt{120}} \right] \\ & \approx 0,5123;0,6877] \end{array}$$
2. Que peut penser le restaurateur de l'affirmation de l'ostréiculteur ?
La fréquence observée est $f = \dfrac{65}{120} \approx 0,5417 \in I_{120}$.
L’ostréiculteur a donc raison d’affirmer que $60\%$ de ses huitres ont une masse supérieure à $91$g avec une marge d’erreur de $5\%$.