Baccalauréat S Nouvelle-Calédonie 7 mars 2014 - Correction de l'Exercice 4

Page 8 sur 9: Correction de l'Exercice 4

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Soit ABCDEFGH un parallélépipède rectangle tel que AB = 2, AD = 3 et AE = 1. On appelle respectivement I, J et P les milieux respectifs des segments [CD], [EF] et [AB]. On note Q le point défini par $\vec{\text{AQ}}= \dfrac{1}{3}\vec{\text{AD}}$.


On appelle plan médiateur d'un segment le plan perpendiculaire à ce segment et passant par son milieu.
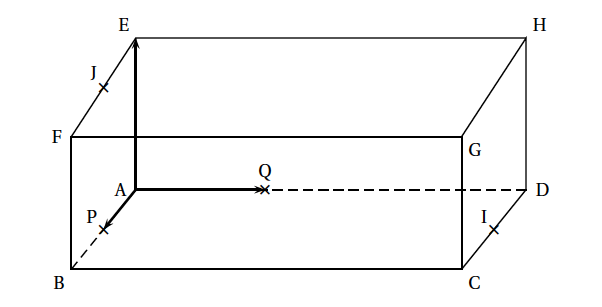
L'objectif de l'exercice est de déterminer les coordonnées du centre d'une sphère circonscrite au tétraèdre ABIJ (c'est-à-dire une sphère qui passe par les quatre points A, B, I, J). L'espace est rapporté au repère orthonormal $\left(\text{A} ; \vec{\text{AP}}, \vec{\text{AQ}}, \vec{\text{AE}}\right)$.

1. Justifier que les quatre points A, B, I et J ne sont pas coplanaires.
Les points A, B et I appartiennent au plan (ABC); comme J est sur l'arête [EF] qui est strictement parallèle au plan (ABC), le point J n'appartient pas au plan (ABC).

Donc les quatre points A, B, I et J ne sont pas coplanaires.
1. Déterminer une équation cartésienne du plan médiateur $\left(P_{1}\right)$ du segment [AB].
Le plan médiateur $\left(P_{1}\right)$ du segment [AB] est le plan perpendiculaire à [AB] passant par le milieu P de [AB]; c'est donc l'ensemble des points M de l'espace tels que les vecteurs $\vec{\text A \text B}$ et $\vec{\text P \text M}$ soient orthogonaux.

Dans le repère $\left(\text{A}~;~\vec{\text{AP}},~\vec{\text{AQ}},~\vec{\text{AE}}\right)$, A a pour coordonnées $(0\:; 0\:; 0)$ et B a pour coordonnées $(2\:; 0\:; 0)$, donc $\vec{\text{AB}}$ a pour coordonnées $(2\:; 0\:; 0)$.

Le point M a pour coordonnées $(x\:; y\:; z)$ et le point P a pour coordonnées $(1\:; 0\:; 0)$, donc $\vec{\text{PM}}$ a pour coordonnées $(x-1\:; y\:; z)$.

$\vec{\text{AB}}$ et $\vec{\text{PM}}$ sont orthogonaux si et seulement si $\vec{\text{AB}}.\vec{\text{PM}}=0 \iff (x-1)\times 2 + y\times 0 + z\times 0 = 0 \iff x-1=0$

Le plan $\left (P_1\right )$ a pour équation $x-1=0$.

On peut aussi justifier que le plan médiateur du segment [AB] est le plan (PIJ) et que les trois points P, I et J ont pour abscisse 1; donc une équation du plan (PIK) est $x=1$.
1. Soit $\left(P_{2}\right)$ le plan d'équation cartésienne $3y - z - 4 = 0$.
   Montrer que le plan $\left(P_{2}\right)$ est le plan médiateur du segment [IJ].
Soit $\left(P_{2}\right)$ le plan d'équation cartésienne $3y - z - 4 = 0$.

D'après le texte, $\vec{\text{AD}}=3 \vec{\text{AQ}}$; or le point Q a pour coordonnées $\left (0\:; 1\:; 0\right )$ donc le point D a pour coordonnées $\left (0\:; 3\:; 0\right )$.

$\vec{\text{AC}} = \vec{\text{AD}} + \vec{\text{DC}} = \vec{\text{AD}} + \vec{\text{AB}}$; or $\vec{\text{AB}}$ a pour coordonnées $\left (2\:; 0\:; 0\right )$ donc $\vec{\text{AC}}$ a pour coordonnées $\left (2\:; 3\:; 0\right )$.

Ce sont aussi les coordonnées du point C. Le point I est le milieu de [CD] donc le point I a pour coordonnées $\left ( \dfrac{0+2}{2}\:; \dfrac{3+3}{2}\:; \dfrac{0+0}{2}\right )$ soit $\left (1\:; 3\:; 0\right )$.

On calcule de même les coordonnées du point J, milieu de [EF], et on trouve $\left (1\:; 0\:; 1\right )$

Un point M de coordonnées $(x\:; y\:; z)$ appartient au plan médiateur de [IJ] si et seulement si IM=JM autrement dit IM$^2=$JM$^2$.

IM$^2 = (x-1)^2+(y-3)^2+z^2$; JM$^2 = (x-1)^2+y^2+(z-1)^2$ IM$^2=$JM$^2 \iff (x-1)^2+(y-3)^2+z^2 = (x-1)^2+y^2+(z-1)^2 \iff y^2-6y+9+z^2 = y^2+z^2-2z+1 \iff -6y +2z +8=8 \iff 3y-z-4=0$

Le plan médiateur de [IJ] a pour équation $3y-z-4=0$ donc c'est le plan $\left (P_2\right )$.
1. 1. Démontrer que les plans $\left(P_{1}\right)$ et $\left(P_{2}\right)$ sont sécants.
   Le plan $\left (P_1\right )$ d'équation $x-1=0$ a pour vecteur normal le vecteur $\vec{n_1}$ de coordonnées $(1\:; 0\:; 0)$.
   
   
   Le plan $\left (P_2\right )$ d'équation $3y-z-4=0$ a pour vecteur normal le vecteur $\vec{n_2}$ de coordonnées $(0\:; 3\:; -1)$.
   
   
   Les vecteurs $\vec{n_1}$ et $\vec{n_2}$ ne sont pas colinéaires donc les plans $\left (P_1\right )$ et $\left (P_2\right )$ ne sont pas parallèles.
   
   
   Les plans $\left (P_1\right )$ et $\left (P_2\right )$ sont donc sécants.
   1. Montrer que leur intersection est une droite $(\Delta)$ dont une représentation paramétrique est \[\left\{\begin{array}{l c l} x &=& 1\\ y &=& t\\ z &=& 3t - 4 \end{array}\right.  \text{ où }  t  \text{décrit l'ensemble des nombres réels }  \mathbb{R}.\]
   Pour déterminer la droite d'intersection des plans $\left (P_1\right )$ et $\left (P_2\right )$, on résout le système $\left\lbrace \begin{array}{r @{\;=\;} l} x-1 & 0\\ 3y-z-4 & 0 \end{array} \right. $
   
   
   que l'on écrit $\left\lbrace \begin{array}{r l} x =& 1\\ y =& y\\ z =& 3y-4 \end{array} \right. $
   
   
   Donc la droite $(\Delta)$ d'intersection des plans $\left (P_1\right )$ et $\left (P_2\right )$ a pour représentation paramétrique: $\left\{\begin{array}{l  l} x =& 1\\ y= & t\\ z =& 3t - 4 \end{array}\right.\: \text{où }\: t \in \mathbb{R}$.
   1. Déterminer les coordonnées du point $\Omega$ de la droite $(\Delta)$ tel que $\Omega$A = $\Omega$I.
   Un point de $(\Delta)$ a pour coordonnées $(1\:; t\:; 3t-4)$ où $t$ est un réel.
   
   
   On va donc chercher une valeur de $t$ pour laquelle $\Omega$A=$\Omega$I, le point $\Omega$ étant un point de $(\Delta)$,
   
   
   autrement dit pour laquelle $\Omega\text A^2 = \Omega\text I^2$. $\Omega \text A^2 = (-1)^2+(-t)^2+ (-3t+4)^2$; $\Omega \text I^2 = (1-1)^2+(3-t)^2+ (-3t+4)^2$ $\Omega\text A^2 = \Omega\text I^2 \iff (-1)^2+(-t)^2+ (-3t+4)^2 = (1-1)^2+(3-t)^2+ (-3t+4)^2 \iff 1+t^2 = 9-6t + t^2 \iff 6t=8 \iff t=\dfrac{4}{3} $
   
   
   Le point $\Omega$ de $(\Delta)$ tel que $\Omega\text A = \Omega\text I$, correspond au paramètre $t=\dfrac{4}{3}$ et a donc pour coordonnées $\left (1\:; \dfrac{4}{3}\:; 3\times \dfrac{4}{3} - 4\right )$ c'est-à -dire $\left (1\:; \dfrac{4}{3}\:; 0\right )$.
   1. Montrer que le point $\Omega$ est centre de la sphère circonscrite au tétraèdre ABIJ.
   Le point $\Omega$ appartient à la droite $(\Delta)$ donc il appartient à la fois à $\left (P_1\right )$ et à $\left (P_2\right )$.
   
   
   $\left (P_1\right )$ est le plan médiateur de [AB] et $\Omega \in \left (P_1\right )$ donc $\Omega$A=$\Omega$B. $\left (P_2\right )$ est le plan médiateur de [IJ] et $\Omega \in \left (P_2\right )$ donc $\Omega$I=$\Omega$J.
   
   
   De plus $\Omega$A=$\Omega$J; donc $\Omega$A=$\Omega$B=$\Omega$I=$\Omega$J: le point $\Omega$ est le centre de la sphère circonscrite au tétraèdre ABIJ.