Baccalauréat S Nouvelle-Calédonie 7 mars 2014

Exercice 1 4 points

Commun à tous les candidats

Cet exercice est un QCM (questionnaire à choix multiple). Pour chaque question, une seule des quatre réponses proposées est exacte.

Le candidat indiquera SUR la copie le numéro de la question et la réponse choisie.

Chaque réponse exacte rapporte un point. Aucune justification n'est demandée. Aucun point n'est enlevé en l'absence de réponse ou en cas de réponse fausse.
Le plan complexe est rapporté au repère orthonormal direct $\left(\text{O},\vec{u},\vec{v}\right)$. Soit $z$ un nombre complexe de la forme $x + \text{i}y$, où $x$ et $y$ sont des réels.

1. Soit $z$ le nombre complexe d'affixe $(1 + \text{i})^4$. L'écriture exponentielle de $z$ est :
   1. $\sqrt{2}\text{e}^{\text{i}\pi}$
   2. $4\text{e}^{\text{i}\pi}$
   3. $\sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}}$
   4. $4\text{e}^{\text{i}\frac{\pi}{4}}$
2. L'ensemble des points $M$ du plan d'affixe $z = x + \text{i}y$ tels que $|z - 1 + \text{i}| = \left|\sqrt{3} - \text{i}\right|$ a pour équation :
   1. $(x - 1)^2 + (y + 1)^2 = 2$
   2. $(x + 1)^2 + (y - 1)^2 = 2$
   3. $(x - 1)^2 + (y + 1)^2 = 4$
   4. $y = x + \frac{\sqrt{3} - 1}{2}$
3. On considère la suite de nombres complexes $\left(Z_{n}\right)$ définie pour tout entier naturel $n$ par $Z_{0} = 1 + \text{i}$ et $Z_{n+1} = \frac{1 + \text{i}}{2}Z_{n}$. On note $M_{n}$ le point du plan d'affixe $Z_{n}$.
   1. Pour tout entier naturel $n$, le point $M_{n}$ appartient au cercle de centre O et de rayon $\sqrt{2}$.
   2. Pour tout entier naturel $n$, le triangle O$M_{n}M_{n + 1}$ est équilatéral.
   3. La suite $\left(U_{n}\right)$ définie par $U_{n} = \left|Z_{n}\right|$ est convergente.
   4. Pour tout entier naturel $n$, un argument de $\dfrac{Z_{n+1} - Z_{n}}{Z_{n}}$ est $\frac{\pi}{2}$.
4. Soit A, B, C trois points du plan complexe d'affixes respectives :
   \[Z_{\text{A}}= - 1 - \text{i} \quad ;\quad Z_{\text{B}} = 2 - 2\text{i}\quad \text{et}\quad Z_{\text{C}} = 1 + 5\text{i}.\]
   On pose $Z = \dfrac{Z_{\text{C}} - Z_{\text{A}}}{Z_{\text{B}} - Z_{\text{A}}}$.
   1. $Z$ est un nombre réel.
   2. Le triangle ABC est isocèle en A.
   3. Le triangle ABC est rectangle en A.
   4. Le point $M$ d'affixe $Z$ appartient à la médiatrice du segment [BC].

Correction de l'exercice 1 (4 points)

Commun à tous les candidats

Cet exercice est un QCM (questionnaire à choix multiple). Pour chaque question, une seule des quatre réponses proposées est exacte.

Le candidat indiquera SUR la copie le numéro de la question et la réponse choisie.

Chaque réponse exacte rapporte un point. Aucune justification n'est demandée. Aucun point n'est enlevé en l'absence de réponse ou en cas de réponse fausse.
Le plan complexe est rapporté au repère orthonormal direct $\left(\text{O},\vec{u},\vec{v}\right)$. Soit $z$ un nombre complexe de la forme $x + \text{i}y$, où $x$ et $y$ sont des réels.

1. Soit $z$ le nombre complexe d'affixe $(1 + \text{i})^4$. L'écriture exponentielle de $z$ est :
   1. $\sqrt{2}\text{e}^{\text{i}\pi}$
   2. $4\text{e}^{\text{i}\pi}$
   3. $\sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}}$
   4. $4\text{e}^{\text{i}\frac{\pi}{4}}$
Le nombre $1+\text{i}$ a pour écriture complexe $\sqrt{2} \text{e}^{\text{i}\frac{\pi}{4}}$ donc le nombre $\left (1+\text{i}\right )^4$ a pour écriture complexe $\left (\sqrt 2\right )^4 \text{e}^{\text{i} 4\frac{\pi}{4}} = 4 \text{e}^{\text{i}\pi}$.

Réponse b.

: $4 \text{e}^{\text{i} \pi}$
1. L'ensemble des points $M$ du plan d'affixe $z = x + \text{i}y$ tels que $|z - 1 + \text{i}| = \left|\sqrt{3} - \text{i}\right|$ a pour équation :
   1. $(x - 1)^2 + (y + 1)^2 = 2$
   2. $(x + 1)^2 + (y - 1)^2 = 2$
   3. $(x - 1)^2 + (y + 1)^2 = 4$
   4. $y = x + \frac{\sqrt{3} - 1}{2}$
Si on appelle $A$ le nombre d'affixe $1-\text{i}$, l'équation $|z - 1 + \text{i}| = \left|\sqrt{3} - \text{i}\right|$ équivaut à $\left| z-z_A \right | = \left | \sqrt 3 - \text{i}\right|$, ou encore $\left| z-z_A \right |^2 = \left | \sqrt 3 - \text{i}\right|^2 \iff \left| z-z_A \right |^2 = 4$.

Réponse c.

: $(x - 1)^2 + (y + 1)^2 = 4$
1. On considère la suite de nombres complexes $\left(Z_{n}\right)$ définie pour tout entier naturel $n$ par $Z_{0} = 1 + \text{i}$ et $Z_{n+1} = \frac{1 + \text{i}}{2}Z_{n}$. On note $M_{n}$ le point du plan d'affixe $Z_{n}$.
   1. Pour tout entier naturel $n$, le point $M_{n}$ appartient au cercle de centre O et de rayon $\sqrt{2}$.
   2. Pour tout entier naturel $n$, le triangle O$M_{n}M_{n + 1}$ est équilatéral.
   3. La suite $\left(U_{n}\right)$ définie par $U_{n} = \left|Z_{n}\right|$ est convergente.
   4. Pour tout entier naturel $n$, un argument de $\dfrac{Z_{n+1} - Z_{n}}{Z_{n}}$ est $\frac{\pi}{2}$.
$Z_{n+1} = \dfrac{1 + \text{i}}{2}Z_{n} \Longrightarrow \left | Z_{n+1}\right | = \left |\dfrac{1 + \text{i}}{2}Z_{n}\right | \iff \left | Z_{n+1}\right | = \left |\dfrac{1 + \text{i}}{2}\right | \times \left | Z_{n}\right | \iff \left | Z_{n+1}\right | = \dfrac{\sqrt{2}}{2} \left | Z_{n}\right | $

Réponse c.

: la suite $\left(U_{n}\right)$ définie par $U_{n} = \left|Z_{n}\right|$ est convergente.
1. Soit A, B, C trois points du plan complexe d'affixes respectives :
   \[Z_{\text{A}}= - 1 - \text{i} \quad ;\quad Z_{\text{B}} = 2 - 2\text{i}\quad \text{et}\quad Z_{\text{C}} = 1 + 5\text{i}.\]
   On pose $Z = \dfrac{Z_{\text{C}} - Z_{\text{A}}}{Z_{\text{B}} - Z_{\text{A}}}$.
   1. $Z$ est un nombre réel.
   2. Le triangle ABC est isocèle en A.
   3. Le triangle ABC est rectangle en A.
   4. Le point $M$ d'affixe $Z$ appartient à la médiatrice du segment [BC].
AB$ = \left |z_{\text B}-z_{\text A}\right | = \sqrt{10}$; AC$ = 2\sqrt{10}$ et BC$ = 5\sqrt{2}$; $\text{BC}^2 = \text{AB}^2 + \text{AC}^2$ d'où la réponse

c.
Réponse c.

: ABC est rectangle en A.

Exercice 2 6 points

Commun à tous les candidats

Partie A
Restitution organisée des connaissances

L'objectif de cette partie est de démontrer le théorème suivant :

Si $X$ est une variable aléatoire suivant la loi normale centrée réduite, alors pour tout réel $\alpha$ appartenant à l'intervalle ]0 ;  1[,

il existe un unique réel strictement positif $\chi_{\alpha}$ tel que $P\left(- \chi_{\alpha} < X < \chi_{\alpha}\right) = 1 - \alpha$.

Soit $f$ la fonction définie sur l'ensemble des nombres réels $\mathbb{R}$ par
\[f(t) = \dfrac{1}{\sqrt{2\pi}}\text{e}^{- \frac{t^2}{2}}.\] Soit $H$ la fonction définie et dérivable sur $[0 ; + \infty[$ par
\[H(x) = P(- x \leqslant X \leqslant x) = \displaystyle\int_{- x}^{x} f(t) \text{d}t.\]

1. Que représente la fonction $f$ pour la loi normale centrée réduite ?
2. Préciser $H(0)$ et la limite de $H(x)$ quand $x$ tend vers $+ \infty$.
3. À l'aide de considérations graphiques, montrer que pour tout nombre réel positif $x,  H(x) = 2\displaystyle\int_{0}^{x} f(t) \text{d}t$.
4. En déduire que la dérivée $H'$ de la fonction $H$ sur $[0 ; + \infty[$ est la fonction $2f$ et dresser le tableau de variations de $H$ sur $[0 ; + \infty[$.
5. Démontrer alors le théorème énoncé.

Partie B
Un laboratoire se fournit en pipettes auprès de deux entreprises, notées A et B. 60 % des pipettes viennent de l'entreprise A et 4,6 % des pipettes de cette entreprise possèdent un défaut.

Dans le stock total du laboratoire, 5 % des pièces présentent un défaut. On choisit au hasard une pipette dans le stock du laboratoire et on note :

• $A$ l'évènement : «La pipette est fournie par l'entreprise A » ;
• $B$ l'évènement : «La pipette est fournie par l'entreprise B » ;
• $D$ l'évènement : «La pipette a un défaut ».

 

1. La pipette choisie au hasard présente un défaut ; quelle est la probabilité qu'elle vienne de l'entreprise A ?
2. Montrer que $p(B \cap D) = 0,0224 $.
3. Parmi les pipettes venant de l'entreprise B, quel pourcentage de pipettes présente un défaut ?

Partie C
Une pipette est dite conforme si sa contenance est comprise, au sens large entre 98 millilitres (mL) et 102 mL.

Soit $X$ la variable aléatoire qui à chaque pipette prise au hasard dans le stock d'un laboratoire associe sa contenance (en millilitres).
On admet que $X$ suit une loi normale de moyenne $\mu$ et écart type $\sigma$ tels que $\mu = 100$ et $\sigma^2 = 1,0424 $.

 

• Quelle est alors la probabilité, à $10^{-4}$ près, pour qu'une pipette prise au hasard soit conforme ? On pourra s'aider de la table ci-dessous ou utiliser une calculatrice.
  $$\begin{array}{|c|c|c|c|c|c|}\hline \text{ Contenance } x \text{ (en mL)}& 95 &96 &97 &98 &99\\ \hline P(X \leqslant x) \left(\text{arrondi à } 10^{- 5}\right)&0,00000 &0,00004 &0,00165 &0,02506&0,16368\\ \hline\hline \text{ Contenance } x \text{ (en mL)}&100 &101 &102 &103 &104\\ \hline P(X \leqslant x) \left(\text{arrondi à } 10^{- 5}\right) &0,5 &0,83632 &0,97494 &0,99835 &0,99996\\ \hline \end{array}$$
• Pour la suite, on admet que la probabilité pour qu'une pipette soit non-conforme est $p = 0,05$. On prélève dans le stock du laboratoire des échantillons de pipettes de taille $n$, où $n$ est un entier naturel supérieur ou égal à $100$.
  On suppose que le stock est assez important pour considérer ces tirages comme indépendants.
  Soit $Y_{n}$ la variable aléatoire qui à chaque échantillon de taille $n$ associe le nombre de pipettes non-conformes de l'échantillon.
  1. Quelle est la loi suivie par la variable aléatoire $Y_{n}$ ?
  2. Vérifier que $n \geqslant 30,  np \geqslant 5$ et $n(1 - p) \geqslant 5$.
  3. Donner en fonction de $n$ l'intervalle de fluctuation asymptotique au seuil de 95 % de la fréquence des pipettes non-conformes dans un échantillon.

   

  
  

  Correction de l'exercice 2 (6 points)

  
  Commun à tous les candidats

  Partie A
  Restitution organisée des connaissances

  L'objectif de cette partie est de démontrer le théorème suivant :

  Si $X$ est une variable aléatoire suivant la loi normale centrée réduite, alors pour tout réel $\alpha$ appartenant à l'intervalle ]0 ;  1[,

  il existe un unique réel strictement positif $\chi_{\alpha}$ tel que $P\left(- \chi_{\alpha} < X < \chi_{\alpha}\right) = 1 - \alpha$.
  
  Soit $f$ la fonction définie sur l'ensemble des nombres réels $\mathbb{R}$ par
  \[f(t) = \dfrac{1}{\sqrt{2\pi}}\text{e}^{- \frac{t^2}{2}}.\] Soit $H$ la fonction définie et dérivable sur $[0 ; + \infty[$ par
  \[H(x) = P(- x \leqslant X \leqslant x) = \displaystyle\int_{- x}^{x} f(t) \text{d}t.\]

  1. Que représente la fonction $f$ pour la loi normale centrée réduite ?
  La fonction $f$ représente la fonction de densité de probabilité pour la loi normale centrée réduite.
  2. Préciser $H(0)$ et la limite de $H(x)$ quand $x$ tend vers $+ \infty$.
  $H(0)=\displaystyle\int_0^0f(t)\text{d} t = 0$; et d'après le cours $\displaystyle\lim_{x \to +\infty} H(x)=1$.
  3. À l'aide de considérations graphiques, montrer que pour tout nombre réel positif $x,  H(x) = 2\displaystyle\int_{0}^{x} f(t) \text{d}t$.
  D'après la relation de Chasles: $\displaystyle\int_{-x}^{x}f(t)\text{d} t = \displaystyle\int_{-x}^{0}f(t)\text{d} t + \displaystyle\int_{0}^{x}f(t)\text{d} t$.
  
  
  Mais la fonction $f$ est positive donc $\displaystyle\int_{-x}^{0}f(t)\text{d} t$ est l'aire du domaine hachuré en rouge sur la figure ci-dessous, tandis que $\displaystyle\int_{0}^{x}f(t)\text{d} t$ est l'aire du domaine hachuré en bleu.
  
  
  
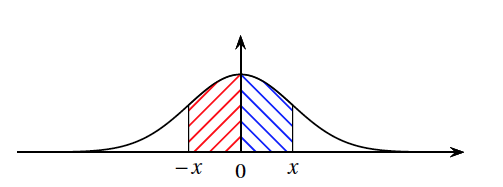
  De plus la fonction $f$ est paire, donc ces deux aires sont égales.
  
  
  Enfin $H(x)$ est l'aire du domaine situé sous la courbe représentant $f$ hachuré en rouge et en bleu sur la figure.
  
  
  Donc $H(x)= \displaystyle\int_{-x}^{x}f(t)\text{d} t = \displaystyle\int_{-x}^{0}f(t)\text{d} t + \displaystyle\int_{0}^{x}f(t)\text{d} t = 2 \displaystyle\int_{0}^{x}f(t)\text{d} t$.
  1. En déduire que la dérivée $H'$ de la fonction $H$ sur $[0 ; + \infty[$ est la fonction $2f$ et dresser le tableau de variations de $H$ sur $[0 ; + \infty[$.
  On sait que la fonction $x \longmapsto \displaystyle\int_{0}^{x} f(t) \text{d} t$ a pour dérivée la fonction $f$; donc la fonction $H$ définie par $H(x)=2 \displaystyle\int_{0}^{x} f(t) \text{d} t$ a pour dérivée la fonction $2f$.
  
  
  Or $f(t) = \dfrac{1}{\sqrt{2\pi} {\text{e}}^{-\frac{t^2}{2}}} > 0$ sur $\mathbb{R}$; comme $H'=2f$, $H'(x)>0$ pour tout réel $x$, et donc la fonction $H$ est strictement croissante sur $[0\:; +\infty[$.
  
  
  On établit le tableau de variations de $H$ sur $[0\:; +\infty[$:
  
  
  1. Démontrer alors le théorème énoncé.
  D'après le tableau de variations, il existe un réel strictement positif unique noté $\chi_\alpha$ tel que $H\left (\chi_\alpha\right ) = 1-\alpha$, donc tel que $P\left (-\chi_\alpha \leq X \leq \chi_\alpha\right ) = 1-\alpha$. Précisons :
  
  
  $$\left.\begin{array}{ll} &\bullet \quad H \text{ est continue sur } I=[0;+\infty[ \text{ (elle est dérivable sur )} I ;\\ &\bullet \quad f \text{ est strictement croissante sur } I ;\\ &\bullet \quad H(0)=0 ;\\ &\bullet \quad \lim\limits_{x \to 0^+} H(x)=1.\\\end{array}\right\}$$ En appliquant le théorème de la bijection sur $[0;+\infty[$ :
  
  
  donc $H$ réalise une bijection de $[0;+\infty[$ sur $[0;1[$. Comme $1-\alpha \in [0;1[$ l'équation $H(x)=1-\alpha$ admet une unique solution $\chi_{\alpha}$ dans $I$

  
  
  Partie B
  Un laboratoire se fournit en pipettes auprès de deux entreprises, notées A et B. 60 % des pipettes viennent de l'entreprise A et 4,6 % des pipettes de cette entreprise possèdent un défaut.

  Dans le stock total du laboratoire, 5 % des pièces présentent un défaut. On choisit au hasard une pipette dans le stock du laboratoire et on note :

  • $A$ l'évènement : «La pipette est fournie par l'entreprise A » ;
  • $B$ l'évènement : «La pipette est fournie par l'entreprise B » ;
  • $D$ l'évènement : «La pipette a un défaut ».

   

  1. La pipette choisie au hasard présente un défaut ; quelle est la probabilité qu'elle vienne de l'entreprise A ?
  La pipette choisie au hasard présente un défaut; la probabilité qu'elle vienne de l'entreprise A est $P_D(A)$.
  
  
  $P_D(A)=\dfrac{P(A\cap D)}{P(D)}=\dfrac{P(A) \times P_A(D)}{P(D)} = \dfrac{0,6 \times 0,046}{0,05} = 0,552$
  1. Montrer que $p(B \cap D) = 0,0224 $.
  D'après la formule des probabilités totales: $P(D)=P(A\cap D)+P(B\cap D) \iff 0,05 = 0,6\times 0,046 + P(B\cap D) \iff 0,05 - 0,0276 = P(B\cap D)$
  
  
  Donc $P(B\cap D)=0,0224$. .
  1. Parmi les pipettes venant de l'entreprise B, quel pourcentage de pipettes présente un défaut ?
  Parmi les pipettes venant de l'entreprise B, la probabilité qu'une pipette présente un défaut est $P_B(D)$.
  
  
  Or $P(B)=1-P(A)=1-0,6=0,4$. $P_B(D) = \dfrac{P(B\cap D)}{P(B)} = \dfrac{0,0224}{0,4} = 0,056$.
  
  
  Parmi les pipettes venant de l'entreprise B, le pourcentage de pipettes présentant un défaut est donc de $5,6\%$

  
  Partie C
  Une pipette est dite conforme si sa contenance est comprise, au sens large entre 98 millilitres (mL) et 102 mL.

  Soit $X$ la variable aléatoire qui à chaque pipette prise au hasard dans le stock d'un laboratoire associe sa contenance (en millilitres).
  On admet que $X$ suit une loi normale de moyenne $\mu$ et écart type $\sigma$ tels que $\mu = 100$ et $\sigma^2 = 1,0424 $.

   

  1. Quelle est alors la probabilité, à $10^{-4}$ près, pour qu'une pipette prise au hasard soit conforme ? On pourra s'aider de la table ci-dessous ou utiliser une calculatrice.
     $$\begin{array}{|c|c|c|c|c|c|}\hline \text{ Contenance } x \text{ (en mL)}& 95 &96 &97 &98 &99\\ \hline P(X \leqslant x) \left(\text{arrondi à } 10^{- 5}\right)&0,00000 &0,00004 &0,00165 &0,02506&0,16368\\ \hline\hline \text{ Contenance } x \text{ (en mL)}&100 &101 &102 &103 &104\\ \hline P(X \leqslant x) \left(\text{arrondi à } 10^{- 5}\right) &0,5 &0,83632 &0,97494 &0,99835 &0,99996\\ \hline \end{array}$$
  On cherche la probabilité qu'une pipette prise au hasard soit conforme, soit $P(98 < X<102)$, en sachant que $X$ suit la loi normale de paramètres $\mu=100$ et $\sigma^2=1,0424$.
  
  
  À la calculatrice, on trouve $0,9499$ à $10^{-4}$ près.
  
  
  En utilisant la table fournie: $P(98<X<102) = P(X<102) - P(X \leq 98) \approx0,97494 -0,02506 \approx 0,94988$
  
  
  Pour la suite, on admet que la probabilité pour qu'une pipette soit non-conforme est $p = 0,05$.
  1. Pour la suite, on admet que la probabilité pour qu'une pipette soit non-conforme est $p = 0,05$. On prélève dans le stock du laboratoire des échantillons de pipettes de taille $n$, où $n$ est un entier naturel supérieur ou égal à $100$.
     On suppose que le stock est assez important pour considérer ces tirages comme indépendants.
     Soit $Y_{n}$ la variable aléatoire qui à chaque échantillon de taille $n$ associe le nombre de pipettes non-conformes de l'échantillon.
     1. Quelle est la loi suivie par la variable aléatoire $Y_{n}$ ?
     Comme on peut supposer que les tirages sont indépendants, la variable aléatoire $Y_n$ suit une loi binomiale de paramètres $n \geq 100$ et $p=0,05$.
     2. Vérifier que $n \geqslant 30,  np \geqslant 5$ et $n(1 - p) \geqslant 5$.
     On sait que $n \geq 100$ donc $n\geq 30$. $n \geq 100$ et $p=0,05$ donc $np \geq 100\times 0,05 \iff np \geq 5$ $p=0,05$ donc $1-p=0,95$; $n(1-p) \geq 100\times 0,95 \iff n(1-p) \geq 95$ et donc $n(1-p) \geq 5$. Les trois conditions sont vérifiées.
     3. Donner en fonction de $n$ l'intervalle de fluctuation asymptotique au seuil de 95 % de la fréquence des pipettes non-conformes dans un échantillon.
     Pour une proportion $p$ et un échantillon de taille $n$, l'intervalle de fluctuation asymptotique au seuil de 95\% est: $$\left[ p- 1,96 \dfrac{\displaystyle \sqrt{p\left(1-p\right)}}{\displaystyle \sqrt{n}}\:;\: p + 1,96\dfrac{\displaystyle \sqrt{p\left(1-p\right)}}{\displaystyle\sqrt{n}} \right]$$ Donc l'intervalle de fluctuation asymptotique au seuil de $95\%$ de la fréquence des pipettes non conformes dans un échantillon est: $$\begin{array}{ll}\\ I &=\left[ 0,05- 1,96 \dfrac{\displaystyle \sqrt{0,05\left(1-0,05\right)}}{\displaystyle \sqrt{n}}\:;\: 0,05 + 1,96\dfrac{\displaystyle \sqrt{0,05\left(1-0,05\right)}}{\displaystyle\sqrt{n}} \right] \\ &=\left[ 0,05- 1,96 \dfrac{\displaystyle \sqrt{0,0475}}{\displaystyle \sqrt{n}}\:;\: 0,05 + 1,96\dfrac{\displaystyle \sqrt{0,0475}}{\displaystyle\sqrt{n}} \right]\\ \end{array}$$
  
  

  Exercice 3 5 points

  
  Commun à tous les candidats

  Partie A
  Soit $f$ la fonction dérivable, définie sur l'intervalle $]0 ; + \infty [$ par
  \[f(x) = x\ln (x).\]
  1. Déterminer les limites de $f$ en $0$ et en $+ \infty$.
  2. On appelle $f'$ la fonction dérivée de $f$ sur $]0 ; + \infty [$. Montrer que $f'(x) = \ln(x) + 1$.
  3. Déterminer les variations de $f$ sur $]0 ; + \infty [$.
  
  Partie B
  Soit $\mathcal{C}$ la courbe représentative de la fonction $f$ dans un repère orthonormal. Soit $\mathcal{A}$ l'aire, exprimée en unités d'aire, de la partie du plan comprise entre l'axe des abscisses, la courbe $\mathcal{C}$ et les droites d'équations respectives $x = 1$ et $x = 2$. On utilise l'algorithme suivant pour calculer, par la méthode des rectangles, une valeur approchée de l'aire $\mathcal{A}$. (voir la figure ci-après).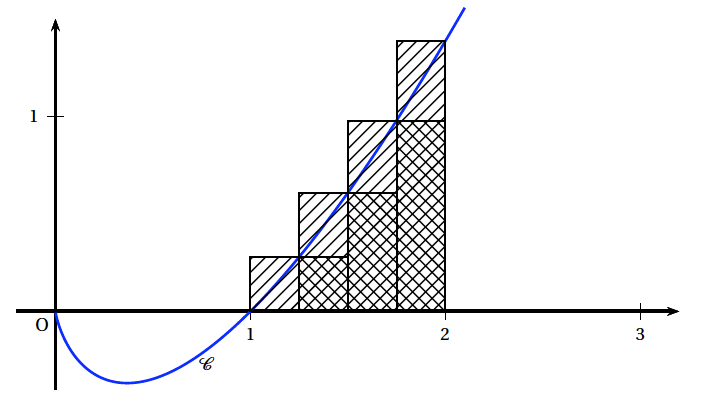
  
    Algorithme :
  $$\begin{array}{|l|l|} \hline \text{Variables}&\\ & k \text{ et } n \text{ sont des entiers naturels }\\ & U, V \text{ sont des nombres réels }\\ \text{Initialisation}&\\ & U \text{ prend la valeur 0}\\ & V \text{ prend la valeur 0}\\ & n \text{ prend la valeur 4 }\\ \text{Traitement}&\\ & \text{Pour } k \text{ allant de 0 à } n - 1\\ & \text{ Affecter à } U \text{ la valeur } U + \frac{1}{n}f\left(1 + \frac{k}{n}\right)\\ & \text{ Affecter à } V \text{ la valeur } V + \frac{1}{n}f\left(1 + \frac{k + 1}{n}\right)\\ & \text{ Fin pour }\\ \text{Affichage} &\\ & \text{ Afficher } U \\ &\text{ Afficher} V\\ \hline \end{array}$$
  
  1. 1. Que représentent $U$ et $V$ sur le graphique précédent ?
     2. Quelles sont les valeurs $U$ et $V$ affichées en sortie de l'algorithme (on donnera une valeur approchée de $U$ par défaut à $10^{-4}$ près et une valeur approchée par excès de $V$ à $10^{-4}$ près) ?
     3. En déduire un encadrement de $\mathcal{A}$.
  2. Soient les suites $\left(U_{n}\right)$ et $\left(V_{n}\right)$ définies pour tout entier $n$ non nul par :
     \[\begin{array}{l c l} U_{n}& =&\dfrac{1}{n}\left[f(1) + f\left(1 + \dfrac{1}{n}\right) + f\left(1 + \dfrac{2}{n}\right) + \cdots + f\left(1 + \dfrac{n-1}{n}\right)\right]\\ V_{n}&=&\dfrac{1}{n}\left[f\left(1 + \dfrac{1}{n}\right) + f\left(1 + \dfrac{2}{n}\right) + \cdots + f\left(1 + \dfrac{n-1}{n}\right) + f(2)\right] \end{array}.\] On admettra que, pour tout $n$ entier naturel non nul, $U_{n} \leqslant \mathcal{A} \leqslant V_{n}$.
     1. Trouver le plus petit entier $n$ tel que $V_{n} - U_{n} < 0,1$.
     2. Comment modifier l'algorithme précédent pour qu'il permette d'obtenir un encadrement de $\mathcal{A}$ d'amplitude inférieure à $0,1$ ?
  Partie C
  Soit $F$ la fonction dérivable, définie sur $]0 ; + \infty[$ par
  \[F(x) = \dfrac{x^2}{2} \ln x - \dfrac{x^2}{4}.\]
  
  1. Montrer que $F$ est une primitive de $f$ sur $]0 ; + \infty[$.
  2. Calculer la valeur exacte de $\mathcal{A}$.

   

  
  

  Exercice 3 5 points

  
  Commun à tous les candidats

  Partie A
  Soit $f$ la fonction dérivable, définie sur l'intervalle $]0 ; + \infty [$ par
  \[f(x) = x\ln (x).\]
  1. Déterminer les limites de $f$ en $0$ et en $+ \infty$.
  D'après le cours, on sait que $\displaystyle\lim_{x \to 0} x\ln(x)=0$ donc $\displaystyle\lim_{x \to 0} f(x)=0$. $$\left. \begin{array}{l} \displaystyle\lim_{x \to +\infty}x = +\infty\\ \displaystyle\lim_{x \to +\infty} \ln(x) = +\infty \end{array} \right\rbrace \displaystyle\lim_{x \to +\infty} x\ln(x) = +\infty $$(par produit) donc $\displaystyle\lim_{x \to +\infty}f(x)=+\infty$.
  2. On appelle $f'$ la fonction dérivée de $f$ sur $]0 ; + \infty [$. Montrer que $f'(x) = \ln(x) + 1$.
  La fonction $f$ est dérivable sur $]0\:; +\infty[$ comme produit de fonctions dérivables: $f'(x)=1\times \ln(x) + x \times \dfrac{1}{x} = \ln(x)+1$.
  3. % Déterminer les variations de $f$ sur $]0~;~+ \infty [$. On étudie le signe de $f'(x)$ sur $]0\:; +\infty[$: $\ln(x)+1>0 \iff \ln(x) >-1 \iff x > \text{e}^{-1}$ Donc:
     • La fonction $f$ est strictement décroissante sur $]0\:; \text{e}^{-1}]$;
     • la fonction $f$ est strictement croissante sur $[\text{e}^{-1}\:; +\infty[$.
  4. Déterminer les variations de $f$ sur $]0 ; + \infty [$.
  
  Partie B
  Soit $\mathcal{C}$ la courbe représentative de la fonction $f$ dans un repère orthonormal. Soit $\mathcal{A}$ l'aire, exprimée en unités d'aire, de la partie du plan comprise entre l'axe des abscisses, la courbe $\mathcal{C}$ et les droites d'équations respectives $x = 1$ et $x = 2$. On utilise l'algorithme suivant pour calculer, par la méthode des rectangles, une valeur approchée de l'aire $\mathcal{A}$. (voir la figure ci-après).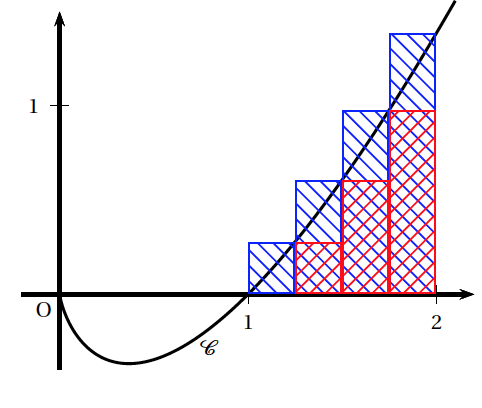
  
    Algorithme :
  $$\begin{array}{|l|l|} \hline \text{Variables}&\\ & k \text{ et } n \text{ sont des entiers naturels }\\ & U, V \text{ sont des nombres réels }\\ \text{Initialisation}&\\ & U \text{ prend la valeur 0}\\ & V \text{ prend la valeur 0}\\ & n \text{ prend la valeur 4 }\\ \text{Traitement}&\\ & \text{Pour } k \text{ allant de 0 à } n - 1\\ & \text{ Affecter à } U \text{ la valeur } U + \frac{1}{n}f\left(1 + \frac{k}{n}\right)\\ & \text{ Affecter à } V \text{ la valeur } V + \frac{1}{n}f\left(1 + \frac{k + 1}{n}\right)\\ & \text{ Fin pour }\\ \text{Affichage} &\\ & \text{ Afficher } U \\ &\text{ Afficher} V\\ \hline \end{array}$$
  
  1. 1. Que représentent $U$ et $V$ sur le graphique précédent ?
     Sur la figure ci-dessus, le nombre $U$ représente la somme des aires des rectangles inférieurs (en rouge); cette somme minore l'aire sous la courbe. Le nombre $V$ représente la somme des aires des rectangles supérieurs (en bleu); cette somme majore l'aire sous la courbe.
     2. Quelles sont les valeurs $U$ et $V$ affichées en sortie de l'algorithme (on donnera une valeur approchée de $U$ par défaut à $10^{-4}$ près et une valeur approchée par excès de $V$ à $10^{-4}$ près) ?
     On fait tourner l'algorithme ci-dessus: $$\begin{array}{|l|c|c|c|c|} \hline \text{Variables }& k & U & V & n \\ \hline \text{Initialisation }& & 0 & 0 & 4\\ \hline \text{Traitement} & 0 & 0 & 0,0698 & 4 \\ & 1 & 0,0697 & 0,2218 & 4 \\ & 2 & 0,2217 & 0,4667 & 4 \\ & 3 & 0,4666 & 0,8132 & 4 \\ \hline \text{Affichage }& \text{On affiche la valeur de } U: &0,4666 &&\\ & \text{ On affiche la valeur de } V: &&0,8132 & \\ \hline \end{array}$$
     3. En déduire un encadrement de $\mathcal{A}$.
     On peut donc en déduire que $0,4666 < \mathcal A < 0,8132$.
  2. Soient les suites $\left(U_{n}\right)$ et $\left(V_{n}\right)$ définies pour tout entier $n$ non nul par :
     \[\begin{array}{l c l} U_{n}& =&\dfrac{1}{n}\left[f(1) + f\left(1 + \dfrac{1}{n}\right) + f\left(1 + \dfrac{2}{n}\right) + \cdots + f\left(1 + \dfrac{n-1}{n}\right)\right]\\ V_{n}&=&\dfrac{1}{n}\left[f\left(1 + \dfrac{1}{n}\right) + f\left(1 + \dfrac{2}{n}\right) + \cdots + f\left(1 + \dfrac{n-1}{n}\right) + f(2)\right] \end{array}.\] On admettra que, pour tout $n$ entier naturel non nul, $U_{n} \leqslant \mathcal{A} \leqslant V_{n}$.
     1. Trouver le plus petit entier $n$ tel que $V_{n} - U_{n} < 0,1$.
     Sachant que $U_{n} = \dfrac{1}{n}\left[f(1) + f\left(1 + \dfrac{1}{n}\right) + f\left(1 + \dfrac{2}{n}\right) + \cdots + f\left(1 + \dfrac{n-1}{n}\right)\right]$ et que
     
     
     $V_{n} = \dfrac{1}{n}\left[f\left(1 + \dfrac{1}{n}\right) + f\left(1 + \dfrac{2}{n}\right) + \cdots + f\left(1 + \dfrac{n-1}{n}\right) + f(2)\right]$,
     
     
     on peut dire que $V_n - U_n = \dfrac{1}{n}\left (f(2)-f(1)\right ) = \dfrac{2\ln(2)-0}{n}= \dfrac{2\ln(2)}{n}$. $V_n-U_n < 0,1 \iff \dfrac{2\ln(2)}{n} < 0,1 \iff 2\ln(2) < 0,1n \iff \dfrac{2\ln(2)}{0,1} < n$
     
     
     Or $\dfrac{2\ln(2)}{0,1} \approx 13,86$
     
     
     donc le plus petit entier $n$ tel que $V_n-U_n$ soit inférieur à 0,1 est 14.
     
     
     Vérification: $V_{13}-U_{13}\approx 0,107 > 0,1$ et $V_{14}-U_{14}\approx 0,099 < 0,1$.
     1. Comment modifier l'algorithme précédent pour qu'il permette d'obtenir un encadrement de $\mathcal{A}$ d'amplitude inférieure à $0,1$ ?
     Pour obtenir un encadrement de $\mathcal{A}$ d'amplitude inférieure à $0,1$ dans l'algorithme, il suffit d'entrer 14 comme valeur de $n$;
     
     
     autrement dit, au lieu de « $n$ prend la valeur 4», on entrera «$n$ prend la valeur 14».
  Partie C
  Soit $F$ la fonction dérivable, définie sur $]0 ; + \infty[$ par
  \[F(x) = \dfrac{x^2}{2} \ln x - \dfrac{x^2}{4}.\]
  
  1. Montrer que $F$ est une primitive de $f$ sur $]0 ; + \infty[$.
  $F'(x)= \dfrac{2x}{2}\times \ln(x) + \dfrac{x^{2}}{2}\times \dfrac{1}{x} -\dfrac{2x}{4}= x\ln(x) +\dfrac{x}{2} - \dfrac{x}{2} = x\ln(x)=f(x)$
  
  
  Donc $F$ est une primitive de $f$ sur $]0\:; +\infty[$.
  1. Calculer la valeur exacte de $\mathcal{A}$.
  La fonction $f$ est croissante sur $[1\:; 2]$ et $f(1)=0$ donc la fonction $f$ est positive sur $[1\:; 2]$;
  
  
  on peut donc dire que $\mathcal A = \displaystyle\int_1^2 f(t) \text{d} t$. $\mathcal A = \displaystyle\int_1^2 f(t) \text{d} t = F(2)-F(1) = \left (2\ln(2)-1\right ) - \left (-\dfrac{1}{4} \right ) = 2\ln(2)-\dfrac{3}{4}$
  
  

  Exercice 4 5 points

  
  Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

  Soit ABCDEFGH un parallélépipède rectangle tel que AB = 2, AD = 3 et AE = 1. On appelle respectivement I, J et P les milieux respectifs des segments [CD], [EF] et [AB]. On note Q le point défini par $\vec{\text{AQ}}= \dfrac{1}{3}\vec{\text{AD}}$.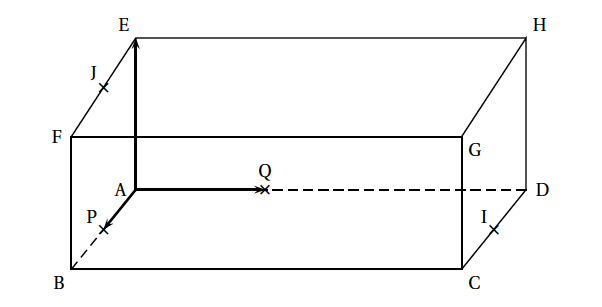
  
  
  On appelle plan médiateur d'un segment le plan perpendiculaire à ce segment et passant par son milieu.
  L'objectif de l'exercice est de déterminer les coordonnées du centre d'une sphère circonscrite au tétraèdre ABIJ (c'est-à-dire une sphère qui passe par les quatre points A, B, I, J). L'espace est rapporté au repère orthonormal $\left(\text{A} ; \vec{\text{AP}}, \vec{\text{AQ}}, \vec{\text{AE}}\right)$.
  
  1. Justifier que les quatre points A, B, I et J ne sont pas coplanaires.
  2. Déterminer une équation cartésienne du plan médiateur $\left(P_{1}\right)$ du segment [AB].
  3. Soit $\left(P_{2}\right)$ le plan d'équation cartésienne $3y - z - 4 = 0$.
     Montrer que le plan $\left(P_{2}\right)$ est le plan médiateur du segment [IJ].
  4. 1. Démontrer que les plans $\left(P_{1}\right)$ et $\left(P_{2}\right)$ sont sécants.
     2. Montrer que leur intersection est une droite $(\Delta)$ dont une représentation paramétrique est \[\left\{\begin{array}{l c l} x &=& 1\\ y &=& t\\ z &=& 3t - 4 \end{array}\right.  \text{ où }  t  \text{décrit l'ensemble des nombres réels }  \mathbb{R}.\]
     3. Déterminer les coordonnées du point $\Omega$ de la droite $(\Delta)$ tel que $\Omega$A = $\Omega$I.
     4. Montrer que le point $\Omega$ est centre de la sphère circonscrite au tétraèdre ABIJ.

   

  
  

  Exercice 4 5 points

  
  Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

  Soit ABCDEFGH un parallélépipède rectangle tel que AB = 2, AD = 3 et AE = 1. On appelle respectivement I, J et P les milieux respectifs des segments [CD], [EF] et [AB]. On note Q le point défini par $\vec{\text{AQ}}= \dfrac{1}{3}\vec{\text{AD}}$.
  
  
  On appelle plan médiateur d'un segment le plan perpendiculaire à ce segment et passant par son milieu.
  L'objectif de l'exercice est de déterminer les coordonnées du centre d'une sphère circonscrite au tétraèdre ABIJ (c'est-à-dire une sphère qui passe par les quatre points A, B, I, J). L'espace est rapporté au repère orthonormal $\left(\text{A} ; \vec{\text{AP}}, \vec{\text{AQ}}, \vec{\text{AE}}\right)$.
  
  1. Justifier que les quatre points A, B, I et J ne sont pas coplanaires.
  Les points A, B et I appartiennent au plan (ABC); comme J est sur l'arête [EF] qui est strictement parallèle au plan (ABC), le point J n'appartient pas au plan (ABC).
  
  
  Donc les quatre points A, B, I et J ne sont pas coplanaires.
  1. Déterminer une équation cartésienne du plan médiateur $\left(P_{1}\right)$ du segment [AB].
  Le plan médiateur $\left(P_{1}\right)$ du segment [AB] est le plan perpendiculaire à [AB] passant par le milieu P de [AB]; c'est donc l'ensemble des points M de l'espace tels que les vecteurs $\vec{\text A \text B}$ et $\vec{\text P \text M}$ soient orthogonaux.
  
  
  Dans le repère $\left(\text{A}~;~\vec{\text{AP}},~\vec{\text{AQ}},~\vec{\text{AE}}\right)$, A a pour coordonnées $(0\:; 0\:; 0)$ et B a pour coordonnées $(2\:; 0\:; 0)$, donc $\vec{\text{AB}}$ a pour coordonnées $(2\:; 0\:; 0)$.
  
  
  Le point M a pour coordonnées $(x\:; y\:; z)$ et le point P a pour coordonnées $(1\:; 0\:; 0)$, donc $\vec{\text{PM}}$ a pour coordonnées $(x-1\:; y\:; z)$.
  
  
  $\vec{\text{AB}}$ et $\vec{\text{PM}}$ sont orthogonaux si et seulement si $\vec{\text{AB}}.\vec{\text{PM}}=0 \iff (x-1)\times 2 + y\times 0 + z\times 0 = 0 \iff x-1=0$
  
  
  Le plan $\left (P_1\right )$ a pour équation $x-1=0$.
  
  
  On peut aussi justifier que le plan médiateur du segment [AB] est le plan (PIJ) et que les trois points P, I et J ont pour abscisse 1; donc une équation du plan (PIK) est $x=1$.
  1. Soit $\left(P_{2}\right)$ le plan d'équation cartésienne $3y - z - 4 = 0$.
     Montrer que le plan $\left(P_{2}\right)$ est le plan médiateur du segment [IJ].
  Soit $\left(P_{2}\right)$ le plan d'équation cartésienne $3y - z - 4 = 0$.
  
  
  D'après le texte, $\vec{\text{AD}}=3 \vec{\text{AQ}}$; or le point Q a pour coordonnées $\left (0\:; 1\:; 0\right )$ donc le point D a pour coordonnées $\left (0\:; 3\:; 0\right )$.
  
  
  $\vec{\text{AC}} = \vec{\text{AD}} + \vec{\text{DC}} = \vec{\text{AD}} + \vec{\text{AB}}$; or $\vec{\text{AB}}$ a pour coordonnées $\left (2\:; 0\:; 0\right )$ donc $\vec{\text{AC}}$ a pour coordonnées $\left (2\:; 3\:; 0\right )$.
  
  
  Ce sont aussi les coordonnées du point C. Le point I est le milieu de [CD] donc le point I a pour coordonnées $\left ( \dfrac{0+2}{2}\:; \dfrac{3+3}{2}\:; \dfrac{0+0}{2}\right )$ soit $\left (1\:; 3\:; 0\right )$.
  
  
  On calcule de même les coordonnées du point J, milieu de [EF], et on trouve $\left (1\:; 0\:; 1\right )$
  
  
  Un point M de coordonnées $(x\:; y\:; z)$ appartient au plan médiateur de [IJ] si et seulement si IM=JM autrement dit IM$^2=$JM$^2$.
  
  
  IM$^2 = (x-1)^2+(y-3)^2+z^2$; JM$^2 = (x-1)^2+y^2+(z-1)^2$ IM$^2=$JM$^2 \iff (x-1)^2+(y-3)^2+z^2 = (x-1)^2+y^2+(z-1)^2 \iff y^2-6y+9+z^2 = y^2+z^2-2z+1 \iff -6y +2z +8=8 \iff 3y-z-4=0$
  
  
  Le plan médiateur de [IJ] a pour équation $3y-z-4=0$ donc c'est le plan $\left (P_2\right )$.
  1. 1. Démontrer que les plans $\left(P_{1}\right)$ et $\left(P_{2}\right)$ sont sécants.
     Le plan $\left (P_1\right )$ d'équation $x-1=0$ a pour vecteur normal le vecteur $\vec{n_1}$ de coordonnées $(1\:; 0\:; 0)$.
     
     
     Le plan $\left (P_2\right )$ d'équation $3y-z-4=0$ a pour vecteur normal le vecteur $\vec{n_2}$ de coordonnées $(0\:; 3\:; -1)$.
     
     
     Les vecteurs $\vec{n_1}$ et $\vec{n_2}$ ne sont pas colinéaires donc les plans $\left (P_1\right )$ et $\left (P_2\right )$ ne sont pas parallèles.
     
     
     Les plans $\left (P_1\right )$ et $\left (P_2\right )$ sont donc sécants.
     1. Montrer que leur intersection est une droite $(\Delta)$ dont une représentation paramétrique est \[\left\{\begin{array}{l c l} x &=& 1\\ y &=& t\\ z &=& 3t - 4 \end{array}\right.  \text{ où }  t  \text{décrit l'ensemble des nombres réels }  \mathbb{R}.\]
     Pour déterminer la droite d'intersection des plans $\left (P_1\right )$ et $\left (P_2\right )$, on résout le système $\left\lbrace \begin{array}{r @{\;=\;} l} x-1 & 0\\ 3y-z-4 & 0 \end{array} \right. $
     
     
     que l'on écrit $\left\lbrace \begin{array}{r l} x =& 1\\ y =& y\\ z =& 3y-4 \end{array} \right. $
     
     
     Donc la droite $(\Delta)$ d'intersection des plans $\left (P_1\right )$ et $\left (P_2\right )$ a pour représentation paramétrique: $\left\{\begin{array}{l  l} x =& 1\\ y= & t\\ z =& 3t - 4 \end{array}\right.\: \text{où }\: t \in \mathbb{R}$.
     1. Déterminer les coordonnées du point $\Omega$ de la droite $(\Delta)$ tel que $\Omega$A = $\Omega$I.
     Un point de $(\Delta)$ a pour coordonnées $(1\:; t\:; 3t-4)$ où $t$ est un réel.
     
     
     On va donc chercher une valeur de $t$ pour laquelle $\Omega$A=$\Omega$I, le point $\Omega$ étant un point de $(\Delta)$,
     
     
     autrement dit pour laquelle $\Omega\text A^2 = \Omega\text I^2$. $\Omega \text A^2 = (-1)^2+(-t)^2+ (-3t+4)^2$; $\Omega \text I^2 = (1-1)^2+(3-t)^2+ (-3t+4)^2$ $\Omega\text A^2 = \Omega\text I^2 \iff (-1)^2+(-t)^2+ (-3t+4)^2 = (1-1)^2+(3-t)^2+ (-3t+4)^2 \iff 1+t^2 = 9-6t + t^2 \iff 6t=8 \iff t=\dfrac{4}{3} $
     
     
     Le point $\Omega$ de $(\Delta)$ tel que $\Omega\text A = \Omega\text I$, correspond au paramètre $t=\dfrac{4}{3}$ et a donc pour coordonnées $\left (1\:; \dfrac{4}{3}\:; 3\times \dfrac{4}{3} - 4\right )$ c'est-à -dire $\left (1\:; \dfrac{4}{3}\:; 0\right )$.
     1. Montrer que le point $\Omega$ est centre de la sphère circonscrite au tétraèdre ABIJ.
     Le point $\Omega$ appartient à la droite $(\Delta)$ donc il appartient à la fois à $\left (P_1\right )$ et à $\left (P_2\right )$.
     
     
     $\left (P_1\right )$ est le plan médiateur de [AB] et $\Omega \in \left (P_1\right )$ donc $\Omega$A=$\Omega$B. $\left (P_2\right )$ est le plan médiateur de [IJ] et $\Omega \in \left (P_2\right )$ donc $\Omega$I=$\Omega$J.
     
     
     De plus $\Omega$A=$\Omega$J; donc $\Omega$A=$\Omega$B=$\Omega$I=$\Omega$J: le point $\Omega$ est le centre de la sphère circonscrite au tétraèdre ABIJ.

   

   

  
  

  Spécialité 5 points

  
  Candidats AYANT SUIVI l'enseignement de spécialité mathématiques