Baccalauréat S Antilles-Guyane septembre 2016 - Correction Spécialité
Page 8 sur 8
Correction de l'exercice de Spécialité 5 points
Parmi les ordinateurs d'un parc informatique, 60% présentent des failles de sécurité. Afin de pallier ce problème, on demande à un technicien d'intervenir chaque jour pour traiter les défaillances. On estime que chaque jour, il remet en état 7% des ordinateurs défaillants, tandis que de nouvelles failles apparaissent chez 3% des ordinateurs sains. On suppose de plus que le nombre d'ordinateurs est constant sur la période étudiée.
Pour tout entier naturel $n$, on note $a_n$ la proportion d'ordinateurs sains de ce parc informatique au bout de $n$ jours d'intervention, et $b_n$ la proportion d'ordinateurs défaillants au bout de $n$ jours. Ainsi $a_0 = 0,4$ et $b_0 = 0,6$.
Partie A
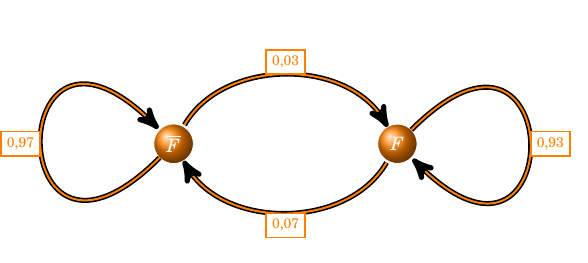
- Décrire la situation précédente à l'aide d'un graphe ou d'un arbre pondéré.
- Déterminer $a_1$ et $b_1$. On a $a_0=0,4$ et $b_0=0,6$
- Pour tout entier naturel $n$, exprimer $a_{n+1}$ et $b_{n+1}$ en fonction de $a_n$ et $b_n$. D’après la formule des probabilités totales on a :
- Soit la matrice $A = \begin{pmatrix}0,97&0,07\\0,03 &0,93\end{pmatrix}$. On pose $X_n = \begin{pmatrix}a_n\\b_n\end{pmatrix}$.
- Justifier que pour tout entier naturel $n, \:X_{n+1} = AX_n$. $AX_n=\begin{pmatrix} 0,97a_n+0,07b_n\\0,03a_n+0,93b_n\end{pmatrix}=X_{n+1}$
- Montrer, par récurrence, que pour tout entier naturel $n,\: X_n = A^n X_0$. Initialisation : Si $n=0$, $A^0X_0=I_2X_0=X_0$ où $I_2$ est la matrice identité.
- Calculer, à l'aide de la calculatrice, $X_{30}$. En donner une interprétation concrète (les coefficients seront arrondis au millième). $X_{30}\approx \begin{pmatrix}0,687\\0,313\end{pmatrix}$
$\quad$
La propriété est vraie au rang $0$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $X_n=A^nX_0$
$X_{n+1}=AX_n=A\times A^nX_0=A^{n+1}X_0$
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ : $X_n=A^nX_0$.
$\quad$
Cela signifie donc, qu’au bout de $30$ jours, $68,7\%$ des ordinateurs n’ont pas de failles de sécurité.
$\quad$
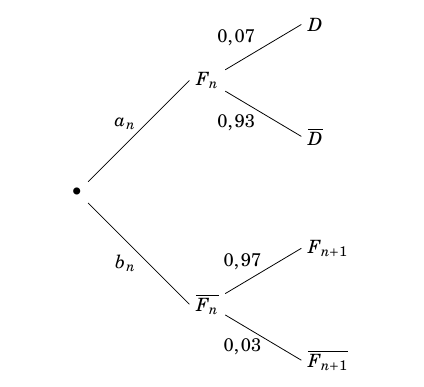
où on appelle $F_n$ l’événement “l’ordinateur est défaillant le jour $n$”.
D’après la formule des probabilités totales on a :
$a_1=0,4\times 0,97+0,6\times 0,07 = 0,43$
Donc $b_1=1-a_1=0,57$.
$a_{n+1}=a_n\times 0,97+b_n\times 0,07$ et $b_{n+1}=a_n\times 0,03+b_n\times 0,93$.
$\quad$
Partie B
- On pose $D = \begin{pmatrix}0,9&0\\0 &0,9\end{pmatrix}$ et $B = \begin{pmatrix}0,07\\ 0,03\end{pmatrix}$.
- Justifier que, pour tout entier naturel $n,\: a_{n+1} + b_{n+1} = 1$. A tout instant, un ordinateur présente ou ne présente pas de failles de sécurité donc $a_{n+1}+b_{n+1}=1$ pour tout entier naturel $n$.
- Montrer que, pour tout entier naturel $n$, \[X_{n+1} = DX_n + B.\] $DX_n+B=\begin{pmatrix}0,9a_n+0,07\\0,09b_n+0,03\end{pmatrix}$
$\quad$
Or :
$\begin{align*} a_{n+1}&=0,97a_n+0,07b_n \\ &=0,97a_n+0,07\left(1-a_n\right) \\ &=0,07-0,9a_n
\end{align*}$
Et
$\begin{align*} b_{n+1}a&=0,03a_n+0,93b_n\\ &=0,03\left(1-b_n\right)+0,93b_n \\ &=0,03+0,9b_n
\end{align*}$
Pour tout entier naturel $n$, on a $X_{n+1}=DX_n+B$.
$\quad$ - On pose, pour tout entier naturel $n$, $Y_n = X_n - 10B$.
- Montrer que pour tout entier naturel $n$, $Y_{n+1} = DY_n$.
- On admet que pour tout entier naturel $n$, $Y_n = D^nY_0$. En déduire que pour tout entier naturel $n$, \:$X_n = D^n\left(X_0 - 10B\right) + 10B$. Pour tout entier naturel $n$ on a :
- Donner l'expression de $D^n$ puis en déduire $a_{n+1}$ et $b_{n+1}$ en fonction de $n$. Pour tout entier naturel $n$ on a $D^n=\begin{pmatrix}0,9^n&0\\0&0,9^n\end{pmatrix}$
$$\begin{align*}Y_{n+1}&=X_{n+1}-10B \\ &=DX_n+B-10B\\ &=DX_n-9B\\ &=DX_n-10DB\\ &=D\left(X_n-10B\right)\\ &=DY_n
\end{align*}$$
$X_n=Y_n+10B=D^nY_0+10B=D^n\left(X_0-10B\right)+10B$
$\quad$
Donc $a_{n+1}=0,9^n(0,4-0,7)+0,7 = -0,3\times 0,9^n+0,7$
Et $b_{n+1}=0,9^n(0,6-0,3)+0,3=0,3\times 0,9^n+0,3$
$\quad$ - Selon cette étude, que peut-on dire de la proportion d'ordinateurs défaillants sur le long terme ? $-1<0,9<1$ donc $\lim\limits_{n \to +\infty} 0,9^n = 0$
Par conséquent $\lim\limits_{n \to +\infty} a_n=0,7$ et $\lim\limits_{n \to +\infty} b_n=0,3$.
Sur le long terme, $70\%$ des ordinateurs seront sains et $30\%$ présenteront des failles de sécurité.
- Vues: 27319
