Baccalauréat S Antilles-Guyane septembre 2016 - Correction Exercice 2

Page 4 sur 8: Correction Exercice 2

Correction de l'exercice 2 (3 points)

Commun à tous les candidats

On considère un cube ABCDEFGH de côté 1.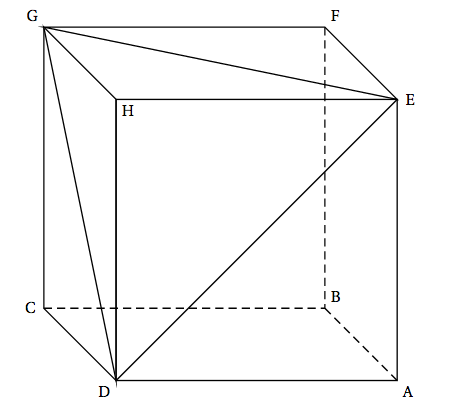

On se place dans le repère orthonormé $\left(\text{B}~;~\vec{\text{BA}},\: \vec{\text{BC}},\: \vec{\text{BF}}\right)$.

1. Déterminer une représentation paramétrique de la droite (BH).
Dans le repère orthonormé $\left(B;\vec{BA},\vec{BC},\vec{BF}\right)$ on a $B(0;0;0)$ et $H(1;1;1)$.
Ainsi $\vec{BH}(1;1;1)$.
Une équation paramétrique de la droite $(BH)$ est donc $\begin{cases} x=t\\y=t \qquad t\in\mathbb R\\z=t\end{cases}$.
$\quad$
2. Démontrer que la droite (BH) est perpendiculaire au plan (DEG).
On a $D(1;1;0)$, $E(1;0;1)$ et $G(0;1;1)$
Ainsi $\vec{DE}(0;-1;1)$ et $\vec{DG}(-1;0;1)$.
Par conséquent $\vec{BH}.\vec{DE}=0-1+1=0$ et $\vec{BH}.\vec{DG}=-1+0+1=0$.
Les deux vecteurs $\vec{DE}$ et $\vec{DG}$ ne sont clairement pas colinéaires.
Par conséquent, le vecteur $\vec{BH}$ est orthogonal à deux vecteurs non colinéaires du plan $(DEG)$ : la droite $(BH)$ est donc perpendiculaire au plan $(DEG)$.
$\quad$
3. Déterminer une équation cartésienne du plan (DEG).
Le vecteur $\vec{BH}$ est normal au plan $(DEG)$.
Une équation cartésienne de ce plan est donc de la forme : $$x+y+z+d=0$$
Le point $D$ appartient à ce plan. Ses coordonnées vérifient alors son équation.
Ainsi $1+1+0+d=0$ et $d=-2$.
Une équation cartésienne de $(DEG)$ est donc $x+y+z-2=0$.
$\quad$
4. On note P le point d'intersection du plan (DEG) et de la droite (BH). Déduire des questions précédentes les coordonnées du point P.
Le point $P(x;y;z)$ vérifient à la fois l’équation cartésienne du plan $(DEG)$ et l’équation paramétrique de la droite $(BH)$.
par conséquent, en injectant les équations paramétriques dans l’équation cartésienne, on obtient :
$t+t+t-2=0$ doit $t=\dfrac{2}{3}$
Cela signifie, par conséquent, que les coordonnées de $P$ sont $\left(\dfrac{2}{3};\dfrac{2}{3};\dfrac{2}{3}\right)$.
$\quad$
5. Que représente le point P pour le triangle DEG ? Justifier la réponse.
Montrons que $P$ est le centre de gravité du triangle $DEG$.
On appelle $I$ le milieu du segment $[DE]$
Ainsi $I\left(1;\dfrac{1}{2};\dfrac{1}{2}\right)$
Et $\vec{GI}\left(1;-\dfrac{1}{2};-\dfrac{1}{2}\right)$
Or $\vec{GP}\left(\dfrac{2}{3};-\dfrac{1}{3};-\dfrac{1}{3}\right)$.
Par conséquent $\vec{GP}=\dfrac{2}{3}\vec{GI}$.
$P$ est bien le centre de gravité du triangle $DEG$.
$\quad$
Chacun des côtés du triangle $DEG$ est une diagonale d’une face du cube. Le triangle $DEG$ est donc équilatéral.
Par conséquent $P$ est aussi le centre du cercle circonscrit au triangle, son orthocentre et le centre de son cercle inscrit.