Baccalauréat S Antilles-Guyane septembre 2016 - Correction Exercice 1
Page 2 sur 8
Correction de l'exercice 1 (6 points)
Le plan est muni d'un repère orthonormal $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$. Pour tout entier naturel $n$, on considère la fonction $f_n$ définie et dérivable sur l'ensemble des nombres réels $\mathbb R$ par \[f_n(x) = \dfrac{\text{e}^{-(n-1)x}}{1 + \text{e}^{x}}.\] On désigne par $\mathcal{C}_n$ la courbe représentative de $f_n$ dans le repère $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$. On a représenté ci-dessous les courbes $\mathcal{C}_n$ pour différentes valeurs de $n$. Soit la suite $\left(u_n\right)$ définie pour tout entier naturel $n$ par : \[u_n = \displaystyle\int_0^1 f_n(x)\:\text{d}x.\] Figure
Partie A - Étude graphique
- Donner une interprétation graphique de $u_n$. $u_n$ correspond à l’aire du domaine compris entre l’axe des abscisses, la courbe $\mathcal{C}_n$ et les droites d’équation $x=0$ et $x=1$.
- Quelles conjectures peut-on faire concernant les variations et la convergence de la suite $\left(u_n\right)$ ? Il semblerait que la suite $\left(u_n\right)$ soit décroissante et converge vers $0$.
- Proposer, à l'aide du graphique et en expliquant la démarche, un encadrement de $u_4$ d'amplitude $0,05$.
$\quad$
$\quad$
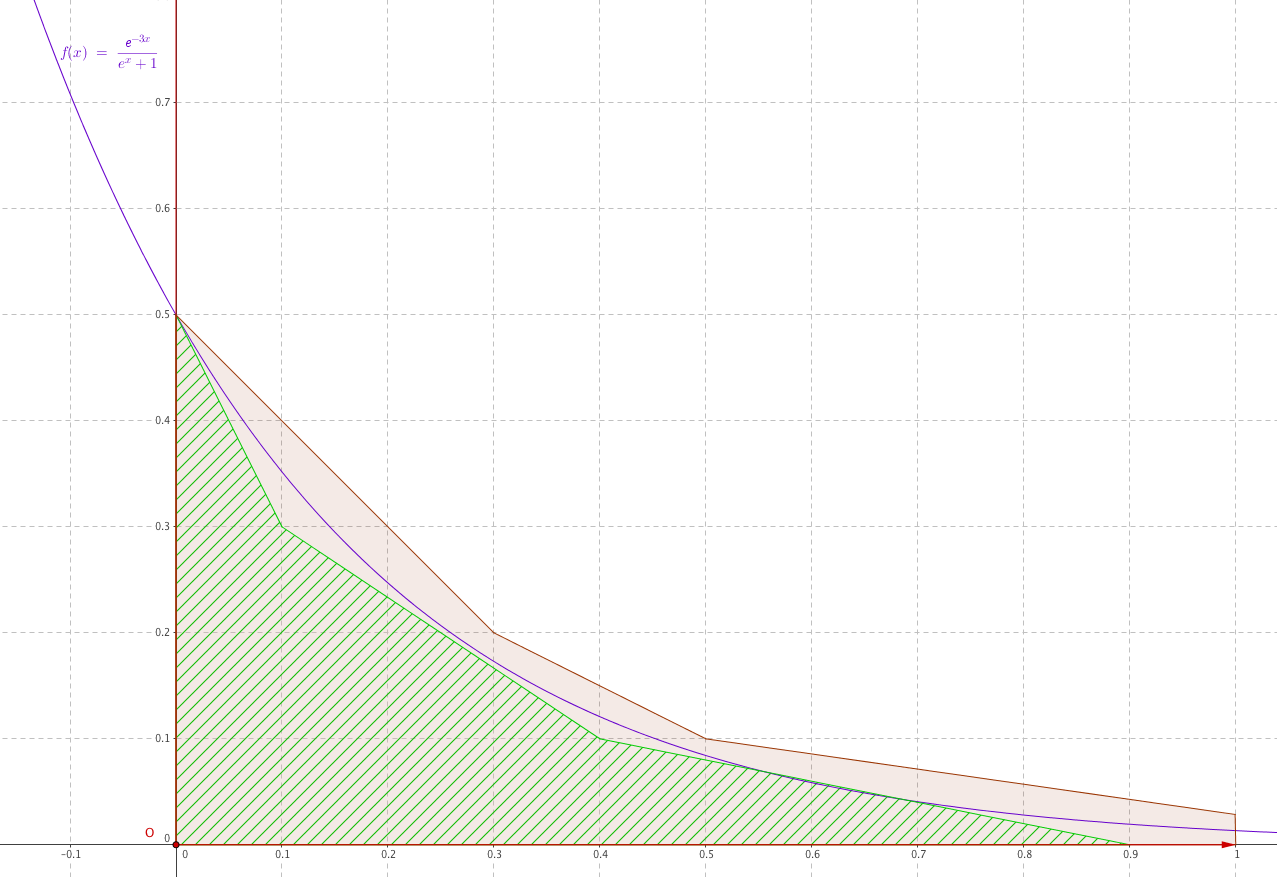
L’aire de la surface verte s’obtient comme la somme des aires de deux trapèzes et d’un triangle : $4+6+2,5=12,5$ carrés d’aire 0,01.
L’aire de la surface limitée par les axes et la ligne marron se décompose en $10,5+3+3,5=17$ aires de carrés d’aire 0,01.
On en déduit que $0,125 <u_4 < 0,17$.
On a donc $$0,12<u_4<0,17$$
Partie B - Étude théorique
- Montrer que $u_0 = \ln \left(\frac{1 + \text{e}}{2}\right)$. $\quad$$$\begin{align*} u_0 &=\int_0^1 \dfrac{\text{e}^ {-(0-1)x}}{1+\text{e}^ x}\text{d}x \\ &=\int_0^1 \dfrac{\text{e}^ x}{1+\text{e}^ x}\text{d}x \\ &=\Big[\ln\left(1+\text{e}^ x\right)\Big]_0^1 \\ &=\ln(1+\text{e})-\ln 2\\ &=\ln \left(\dfrac{1+\text{e}}{2}\right)
- Montrer que $u_0 + u_1 = 1$ puis en déduire $u_1$. $$\begin{align*} u_0+u_1&=\int_0^1 \dfrac{\text{e}^ {-(0-1)x}}{1+\text{e}^ x}\text{d}x + \int_0^1 \dfrac{\text{e}^ {-(1-1)x}}{1+\text{e}^ x}\text{d}x\\ &=\int_0^1 \dfrac{\text{e}^ {x}}{1+\text{e}^ x}\text{d}x + \int_0^1 \dfrac{1}{1+\text{e}^ x}\text{d}x \\ &=\int_0^1 \dfrac{1+\text{e}^ {x}}{1+\text{e}^ x}\text{d}x \\ &=\int_0^1 1\text{d}x \\ &=\Big[x\Big]_0^1 \\ &=1-0\\ &=1
- Montrer que, pour tout entier naturel $n$,\: $u_n \geqslant 0$. La fonction exponentielle est une fonction strictement positive.
- On pose pour tout entier naturel $n$ et pour tout $x$ réel, $d_n(x) = f_{n+1}(x) - f_n(x)$.
- Montrer que, pour tout nombre réel $x, d_n(x) = \text{e}^{- nx} \frac{1 - \text{e}^x}{1 + \text{e}^x}$.
- Étudier le signe de la fonction $d_n$ sur l'intervalle [0~;~1]. La fonction exponentielle est strictement positive.
$$\begin{align*} d_n&=f_{n+1}(x)-f_n(x) \\ &=\dfrac{\text{e}^ {-nx}}{1+\text{e}^ x}-\dfrac{\text{e}^ {-(n-1)x}}{1+\text{e}^ x} \\ &=\dfrac{\text{e}^ {-nx}-\text{e}^ {-(n-1)x}}{1+\text{e}^ x} \\ &=\dfrac{\text{e}^ {-nx}\left(1-\text{e}^ x\right)}{1+\text{e}^ x} \\ &=e^{-nx}\dfrac{1-\text{e}^ x}{1+\text{e}^ x}
\end{align*}$$
$\quad$
Par conséquent le signe de $d_n(x)$ ne dépend que de celui de $1-\text{e}^ x$.
Or, pour tout réel $x$ appartenant à l’intervalle $[0;1]$, on a $\text{e}^ x\geq 1$.
Par conséquent, pour tout réel $x$ de l’intervalle $[0;1]$, $d_n(x)\leq 0$.
Sur l’intervalle $[0;1]$, la fonction $d_n$ est donc négative.
$\quad$ - En déduire que la suite $\left(u_n\right)$ est convergente. $u_{n+1}-u_n=\displaystyle \int_0^1 d_n(x)\text{d}x$.
- On note $\ell$ la limite de la suite $\left(u_n\right)$.
- Montrer que, pour tout entier $n$ supérieur ou égal à 1, on a : \[u_n + u_{n + 1} = \dfrac{1 - \text{e}^{- n}}{n}.\]
- En déduire la valeur de $\ell$. D’une part $\lim\limits_{n\to +\infty} u_n+u_{n+1}=2\ell$.
- On souhaite construire un algorithme qui affiche la valeur de $u_N$ pour un entier naturel $N$ non nul donné. Recopier et compléter les quatre lignes de la partie Traitement de l'algorithme suivant. $$\begin{array}{|l l|}\hline \text{Entrée :} &N \text{ est un entier naturel non nul}\\ \text{Variables :} &U \text{ est un nombre réel }\\ &K \text{ est un entier naturel }\\ \text{Initialisation :}& \text{ Affecter 1 à } K\\ &\text{ Affecter } 1 - \ln \left(\frac{1 + \text{e}}{2}\right) \text{ à } U\\ &\text{ Demander à l'utilisateur la valeur de } N\\ \text{Traitement :} & \text{ Tant que } K < N\\ &\text{ Affecter } \ldots \ldots \ldots \text{ à } U\\ &\text{ Affecter } \ldots \ldots \ldots \text{ à } K\\ &\text{ Fin Tant que }\\ \text{Sortie :} &\text{ Afficher } U\\ \hline \end{array}$$ On obtient l’algorithme suivant :
$$\begin{align*} u_n+u_{n+1}&=\int_0^1\dfrac{\text{e}^ {-(n-1)x}}{1+\text{e}^ x}\text{d}x+\int_0^1 \dfrac{\text{e}^ {-nx}}{1+\text{e}^ x} \\ &=\int_0^1\dfrac{\text{e}^ {-(n-1)x}+\text{e}^ {-nx}}{1+\text{e}^ x}\text{d}x \\ &=\int_0^1\dfrac{\text{e}^ {-nx}\left(\text{e}^ {x}+1\right)}{1+\text{e}^ x}\text{d}x \\ &=\int_0^1 \text{e}^ {-nx}\text{d}x \\ &=\Big[-\dfrac{\text{e}^ {-nx}}{n}\Big]_0^1\\ &=-\dfrac{\text{e}^ {-n}}{n}+\dfrac{1}{n}\\ &=\dfrac{1-\text{e}^ {-n}}{n}
\end{align*}$$
$\quad$
D’autre part $\lim\limits_{n \to +\infty} \text{e}^ {-n}=0$ donc $\lim\limits_{n \to +\infty} \dfrac{1-\text{e}^ {-n}}{n}=0$.
Par conséquent $2\ell = 0$ et $\ell = 0$.
$\quad$
Entrée :
$\quad$ $N$ est un entier naturel non nul
Variables :
$\quad$ $U$ est un nombre réel
$\quad$ $K$ est un entier naturel
Initialisation :
$\quad$ Affecter $1$ à $K$
$\quad$ Affecter $1-\ln \left(\dfrac{1+\text{e}}{2}\right)$ à $U$
$\quad$ Demander à l’utilisateur la valeur de $N$
Traitement :
$\quad$ Tant que $K<N$
$\qquad$ Affecter $\dfrac{1-\text{e}^ {-K}}{K}-U$ à $U$
$\qquad$ Affecter $K+1$ à $K$
$\quad$ Fin Tant que
Sortie :
$\quad$ Afficher $U$
$\quad$
\end{align*}$$
$\quad$
\end{align*}$$
Donc $u_1=1-u_0=1-\ln \left(\dfrac{1+\text{e}}{2}\right)$
$\quad$
Par conséquent, pour tout entier naturel $n$ et tout réel $x$ on a $f_n(x) \geq 0$.
On intègre une fonction continue positive sur l’intervalle $[0;1]$.
Par conséquent $u_n \geq 0$.
$\quad$
Puisque $d_n(x) \leq 0$ sur $[0;1]$, cela signifie donc que $u_{n+1}-u_n\leq 0$.
La suite $\left(u_n\right)$ est par conséquent décroissante.
$\quad$
La suite $\left(u_n\right)$ est décroissante et minorée par $0$; elle est donc convergente.
Exercice 2
- Vues: 27313
