Baccalauréat S Amérique du Sud --12 novembre 2018 - Correction Exercice 2
Page 4 sur 12
Correction de l'exercice 2 (4 points)
Lorsque la queue d'un lézard des murailles casse, elle repousse toute seule en une soixantaine de jours. Lors de la repousse, on modélise la longueur en centimètre de la queue du lézard en fonction du nombre de jours. Cette longueur est modélisée par la fonction $f$ définie sur $[0~;~+ \infty[$ par : \[f(x) = 10\text{e}^{u(x)}\] où $u$ est la fonction définie sur $[0~;~+ \infty[$ par : \[u(x) = - \text{e}^{2 - \frac{x}{10}}.\] On admet que la fonction $f$ est dérivable sur $[0~;~+ \infty[$ et on note $f'$ sa fonction dérivée.
- Vérifier que pour tout $x$ positif on a $f'(x) = - u(x)\text{e}^{u(x)}$. En déduire le sens de variations de la fonction $f$ sur $[0~;~+ \infty[$. Pour tout réel $x$ positif on a $ f'(x)=10u'(x)\text{e}^{u(x)}$.
-
- Calculer $f(20)$. En déduire une estimation, arrondie au millimètre, de la longueur de la queue du lézard après vingt jours de repousse. $u(20)=-\text{e}^{2-\frac{20}{10}}=-\text{e}^0=-1$
- Selon cette modélisation, la queue du lézard peut-elle mesurer $11$ cm ? On a $\lim\limits_{x \to +\infty} 2-\dfrac{x}{10}=-\infty$ et $\lim\limits_{X \to -\infty} \text{e}^X=0$.
Donc $f(20)=10\text{e}^{-1} \approx 3,7$
Après vingt jours de repousse la queue mesure environ $3,7$ cm.
$\quad$
Donc $\lim\limits_{x \to +\infty} u(x)=0$.
Par conséquent $\lim\limits_{x \to +\infty} f(x)=10\text{e}^0=10<11$.
La fonction $f$ est strictement croissante sur $[0;+\infty[$ et majorée par $10$.
La queue du lézard ne donc pas mesurer $11$ cm.
$\quad$ - On souhaite déterminer au bout de combien de jours la vitesse de croissance est maximale. On admet que la vitesse de croissance au bout de $x$ jours est donnée par $f'(x)$. On admet que la fonction dérivée $f'$ est dérivable sur $[0~;~+ \infty[$, on note $f''$ la fonction dérivée de $f'$ et on admet que : \[f''(x) = \dfrac{1}{10}u(x)\text{e}^{u(x)}(1 + u(x)).\]
- Déterminer les variations de $f'$ sur $[0~;~+ \infty[$. La fonction exponentielle est strictement positive.
- En déduire au bout de combien de jours la vitesse de croissance de la longueur de la queue du lézard est maximale. La fonction $f’$ atteint donc son maximum quand $x=20$.
Le signe de $f"(x)$ ne dépend donc que de celui de $u(x)\left(1+u(x)\right)$.
On a vu à la question 1. que $u(x)<0$ sur l’intervalle $[0;+\infty[$.
Étudions le signe de $1+u(x)$.
On veut résoudre l’équation
$\begin{align*} 1+u(x)=0&\iff -\text{e}^{2-\frac{x}{10}}=-1 \\
&\iff \text{e}^{2-\frac{x}{10}}=\text{e}^0 \\
&\iff 2-\dfrac{x}{10}=0 \\
&\iff x=20\end{align*}$
De plus
$\begin{align*} 1+u(x)>0&\iff -\text{e}^{2-\dfrac{x}{10}}>-1 \\
&\iff \text{e}^{2-\dfrac{x}{10}}<\text{e}^0 \\
&\iff 2-\dfrac{x}{10}<0 \\
&\iff x>20\end{align*}$
On obtient ainsi le tableau de signes suivant :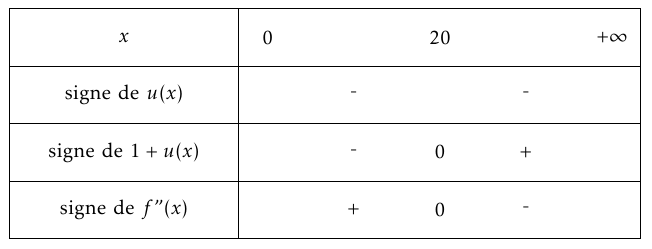
La vitesse de croissance de la longueur de la queue du lézard est maximale au bout de $20$ jours.
$\quad$
Or $u'(x)=-\left(-\dfrac{1}{10}\right)\text{e}^{2-\frac{x}{10}}=-\dfrac{u(x)}{10}$
Par conséquent $f'(x)=-\dfrac{10}{u(x)}\times 10\text{e}^{u(x)} = -u(x)\text{e}^{u(x)}$.
La fonction exponentielle est strictement positive. Le signe de $f'(x)$ ne dépend donc que de celui de $-u(x)$.
Or $u(x)=-\text{e}^{2-\frac{x}{10}}$.
Du fait de la positivité de la fonction exponentielle on a $u(x)<0$ sur $[0;+\infty[$.
Ainsi, $f'(x)>0$ sur l’intervalle $[0;+\infty[$.
La fonction $f$ est donc strictement croissante sur $[0;+\infty[$.
$\quad$
- Vues: 53068
