BAC S 2016 de Mathématiques : Centres Étrangers 8 juin 2016 - Correction Exercice 2

Page 4 sur 10: Correction Exercice 2

Correction de l'exercice 2 (6 points)

Commun à tous les candidats

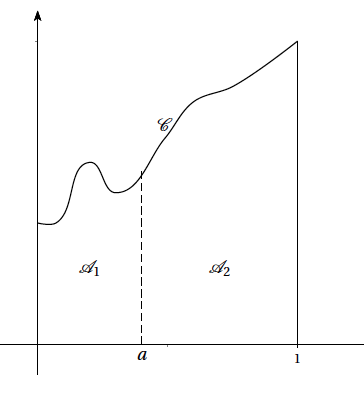
Soit $f$ une fonction définie sur l'intervalle $[0~;~1]$, continue et positive sur cet intervalle, et $a$ une réel tel que $0<a<1$. On note :

$\mathscr{C}$ la courbe représentative de la fonction $f$ dans un repère orthogonal : $\mathscr{A}_1$ l'aire du domaine plan limité par l'axe des abscisses et la courbe $\mathscr{C}$ d'une part, les droites d'équations $x=0$ et $x=a$ d'autre part. $\mathscr{A}_2$ l'aire du domaine plan limité par l'axe des abscisses et la courbe $\mathscr{C}$ d'une part, les droites d'équations $x=a$ et $x=1$ d'autre part.

Figure
Le but de cet exercice est de déterminer, pour différentes fonctions $f$, une valeur du réel $a$ vérifiant la condition (E) : «les aires $\mathscr{A}_1$ et $\mathscr{A}_2$ sont égales». On admet l'existence d'un tel réel $a$ pour chacune des fonctions considérées.

Partie A : Étude de quelques exemples

1. Vérifier que dans les cas suivants, la condition (E) est remplie pour un unique réel $a$ et déterminer sa valeur.
   1. $f$ est une fonction constante strictement positive.
   Si $f$ est constante, il suffit de prendre $a=0,5$.
   $A_1$ et $A_2$ sont les aires de deux rectangles de même longueur et largeur.
   $\quad$
   
   2. $f$ est définie sur $[0~;~1]$ par $f(x)=x$.
   Si $f(x)=x$ sur $[0;1]$.
   On a $A_1=\displaystyle \int_0^a x\mathrm{d}x = \left[\dfrac{x^2}{2}\right]_0^a = \dfrac{a^2}{2}$
   Et $A_2=\displaystyle \int_a^1 x\mathrm{d}x = \left[\dfrac{x^2}{2}\right]_a^1=\dfrac{1-a^2}{2}$.
   On veut donc que $\dfrac{a^2}=\dfrac{1-a^2}{2}$ soit $a^2=1-a^2$ et donc $2a^2=1$ d’où $a^2=\dfrac{1}{2}$.
   Puisque $a>0$ on a alors $a=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}$.
2. 1. À l'aide d'intégrales, exprimer, en unités d'aires, les aires $\mathscr{A}_1$ et $\mathscr{A}_2$.
   On a , puisque la fonction $f$ est continue et positive sur $[0; 1]$ $A_1=\displaystyle \int_0^a f(x)\mathrm{d}x $ et $A_2=\displaystyle \int_a^1 f(x)\mathrm{d}x $.
   $\quad$
   
   2. On note $F$ une primitive de la fonction $f$ sur l'intervalle $[0~;~1]$. Démontrer que si le réel $a$ satisfait la condition (E), alors $F(a)=\dfrac{F(0)+F(1)}{2}$. La réciproque est-elle vraie ?
   Si $F$ est une primitive de $f$ sur $[0;1]$ alors :
   $A_1=F(a)-F(0)$ et $A_2=F(1)-F(a)$.
   $\begin{align*} A_1=A_2 & \iff F(a)-F(0)=F(1)-F(a) \\
   &\iff 2F(a)=F(1)+F(0) \\
   &\iff F(a)=\dfrac{F(1)+F(0)}{2}
   \end{align*}$
   $\quad$
   Il n’y a que des équivalences dans la démarche précédente. La réciproque est donc vraie.
3. Dans cette question, on envisage deux autres fonctions particulières.
   1. La fonction $f$ est définie pour tout réel $x$ de $[0~;~1]$ par $f(x)=\mathrm{e}^{x}$. Vérifier que la condition (E) est vérifiée pour un unique réel $a$ et donner sa valeur.
   Si $f(x)=\text{e}^x$ alors une primitive sur $[0;1]$ est $F$ définie par $F(x)=\text{e}^x$.
   On sait que $F(a)=\dfrac{F(1)+F(0)}{2}$
   On a donc $\text{e}^a=\dfrac{\text{e}^0+\text{e}^1}{2}=\dfrac{1+\text{e}}{2}$.
   Par conséquent $a=\ln \dfrac{1+\text{e}}{2}$.
   $\quad$
   
   2. La fonction $f$ définie pour tout réel $x$ de $\left[0~;~1\right]$ par $f(x)=\dfrac{1}{(x+2)^2}$. Vérifier que la valeur $a=\dfrac{2}{5}$ convient.
   Si $f(x)=\dfrac{1}{(x+2)^2}$ alors une primitive $F$ sur $[0;1]$ est définie par $F(x)=-\dfrac{1}{x+2}$.
   On sait que $F(a)=\dfrac{F(1)+F(0)}{2}$
   Ainsi $\dfrac{1}{a+2}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{2}$
   Donc $\dfrac{1}{a+2}=\dfrac{5}{12}$.
   D’où $5(a+2)=12$.
   Par conséquent $5a+10=12$ et $a=\dfrac{2}{5}$.

 

Partie B : Utilisation d'une suite pour déterminer une valeur approchée de $a$

Dans cette partie, on considère la fonction $f$ définie pour tout réel $x$ de $[0~;~1]$ par $f(x)=4-3x^2$.

1. Démontrer que si $a$ est un réel satisfaisant la condition (E), alors $a$ est solution de l'équation : \[x=\dfrac{x^3}{4}+\dfrac{3}{8}.\] Dans la suite de l'exercice, on admettra que cette équation a une unique solution dans l'intervalle $[0~;~1]$. on note $\alpha$ cette solution.
$f(x)=4-3x^2$
La fonction $F$ définie sur $[0;1]$ par $F(x)=4x-x^3$ est donc une primitive de $f$ sur cet intervalle.
On réutilise la propriété de la question A.2.b.
$4a-a^3=\dfrac{0+(4-1)}{2}$
Soit $4a-a^3=\dfrac{3}{2}$
Donc $8a-2a^3=3$
Ainsi $8a=2a^3+3$
Et par conséquent $a=\dfrac{a^3}{4}+\dfrac{3}{8}$.

2. On considère la fonction $g$ définie pour tout réel $x$ de $[0~;~1]$ par $g(x)=\dfrac{x^3}{4}+\dfrac{3}{8}$ et la suite $\left(u_n\right)$ définie par : $u_0=0$ et, pour tout entier naturel $n$, $u_{n+1}=g\left(u_n\right)$.
   1. Calculer $u_1$.
   $u_1=g(0)=\dfrac{3}{8}$.
   
   2. Démontrer que la fonction $g$ est croissante sur l'intervalle $[0~;~1]$.
   La fonction $g$ est croissante comme somme d’une fonction croissante et d’une fonction constante sur $[0;1]$.
   On peut égaler calculer la dérivée et étudier son signe ....
   3. Démontrer par récurrence que, pour tout entier naturel $n$, on a $0\leqslant u_n\leqslant u_{n+1}\leqslant 1$.
   Initialisation : Si $n=0$.
   Alors $u_0=0$ et $u_1=\dfrac{3}{8}$.
   On a bien $0 \leqslant u_0 \leqslant u_1 \leqslant 1$
   La propriété est donc vraie au rang $0$.
   $\quad$
   Hérédité :On suppose la propriété vraie au rang $n$ : $0\leqslant u_n\leqslant u_{n+1}\leqslant 1$.
   La fonction $g$ est croissante sur l’intervalle $[0;1]$.
   Par conséquent $g(0) \leqslant g\left(u_{n}\right) \leqslant g\left(u_{n+1}\right) \leqslant g(1)$.
   Soit $0 \leqslant \dfrac{3}{8} \leqslant u_{n+1} \leqslant u_{n+2} \leqslant \dfrac{5}{8} \leqslant 1$
   La propriété est donc héréditaire.
   $\quad$
   Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
   Donc pour tout entier naturel $n$ on a : $0\leqslant u_n\leqslant u_{n+1}\leqslant 1$.
   $\quad$
   $\quad$
   
   4. Prouver que la suite $\left(u_n\right)$ est convergente. À l'aide des opérations sur les limites, prouver que la limite est $a$.
   La suite $\left(u_n\right)$ est donc croissante et majorée par $1$; elle converge d'après le théorème de la convergence monotone.
   On appelle $\alpha$ la limite de cette suite.
   Puisque $u_{n+1}=g\left(u_n\right)$ avec $g$ continue sur $\mathbb R$ donc en $\alpha$ cela signifie donc, par passage à la limite, que $\alpha=g(\alpha)$
   et par ailleurs $0\leqslant u_n\leqslant 1$ donc, par passage à la limite, $0\leqslant \alpha \leqslant 1$ .
   Ainsi $\alpha=a$ car d'après l'énoncé l'équation $g(x)=x$ a une unique solution $a$ dans $[0; 1]$.
   $\quad$
   
   5. On admet que le réel $a$ vérifie l'inégalité $0 < a-u_{10} < 10^{-9}$. Calculer $u_{10}$ à $10^{-9}$ près.
   On a, à l’aide de la calculatrice, $u_{10} \approx 0,389~807~84$
   En vidéo !