BAC S 2016 de Mathématiques : Centres Étrangers 8 juin 2016 - Correction Exercice 4

Page 8 sur 10: Correction Exercice 4

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On veut modéliser dans le plan la coquille d'un nautile à l'aide d'une ligne brisée en forme de spirale. on s'intéresse à l'aire délimitée par cette ligne.
On munit le ;plan d'un repère orthormal direct $\left(O~;~\overrightarrow{u}~;~\overrightarrow{v}\right)$. Soit $n$ un entier supérieur ou égal à 2. Pour tout entier $k$ allant de 0 à $n$, on définit les nombres complexes $z_k=\left(1+\dfrac{k}{n}\right)\mathrm{e}^{\mathrm{i}\frac{2k\pi}{n}}$ et on note $M_k$ le point d'affixe $z_k$. Dans ce modèle, le pourtour du nautile est la ligne visée reliant tous les points $M_k$ avec $0\leqslant k\leqslant n$. Par exemple, pour les entiers $n=6$, $n=10$ et $n=20$, on obtient les figures ci-dessous.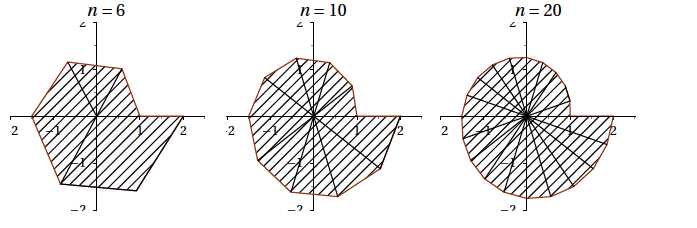

Partie A : Ligne brisée formée à partir de sept points

Dans cette partie, on suppose que $n=6$. Ainsi, pour $0\leqslant k\leqslant 6$, on a $z_k=\left(1+\dfrac{k}{6}\right)\mathrm{e}^{\mathrm{i}\frac{2k\pi}{6}}$.

1. Déterminer la forme algébrique de $z_1$.
$z_1=\left(1+\dfrac{1}{6}\right)\text{e}^{\text{i}\pi/3} = \dfrac{7}{6}\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\text{i}\right)$
Donc $z_1=\dfrac{7}{12}+\dfrac{7\sqrt{3}}{12}\text{i}$
$\quad$
2. Vérifier que $z_0$ et $z_6$ sont des entiers que l'on déterminera.
$z_0=1\text{e}^0\text{i} = 1$ est bien un entier.
$z_6=2\text{e}^{12\text{i}\pi/6}=2\text{e}^{2\text{i}\pi} = 2$ est également un entier.

3. Calculer la longueur de la hauteur issue de $M_1$ dans le triangle $OM_0M_1$ puis établir que l'aire de ce triangle est égale à $\dfrac{7\sqrt{3}}{24}$.
La hauteur issur de $M_1$ dans le triangle $OM_0M_1$ correspond à la partie imaginaire de $z_1$. Elle mesure donc $\dfrac{7\sqrt{3}}{12}$.
L’aire de ce triangle vaut ainsi $\dfrac{\dfrac{7\sqrt{3}}{12} \times 1}{2}=\dfrac{7\sqrt{3}}{24}$.
$\quad$

 

Partie B : Ligne brisée formée à partir de $n+1$ points

Dans cette partie, $n$ est un entier supérieur ou égal à 2.

1. Pour tout entier $k$ tel que $0\leqslant k\leqslant n$, déterminer la longueur $OM_k$.
$OM_k=\left|z_k\right|=1+\dfrac{k}{n}$ pour tout entier $k$ tel que $0\leqslant k\leqslant n$.

2. Pour $k$ entier tel que $0\leqslant k\leqslant n-1$, déterminer une mesure des angles $\left(\overrightarrow{\text{u}}~;~\overrightarrow{OM_k}\right)$ et $\left(\overrightarrow{\text{u}}~;~\overrightarrow{OM_{k+1}}\right)$. En déduire une mesure de l'angle $\left(\overrightarrow{OM_k}~;~\overrightarrow{OM_{k+1}}\right)$.
$\left(\vec{u},\vec{OM_k}\right) = \arg\left(z_k\right) = \dfrac{2k\pi}{n}$ modulo $2\pi$ .
$\left(\vec{u},\vec{OM_{k+1}}\right) = \arg\left(z_{k+1}\right) = \dfrac{2(k+1)\pi}{n}$ modulo $2\pi$.
$\quad$
$\begin{align*} \left(\vec{OM_k},\vec{OM_{k+1}}\right)&= \left(\vec{OM_k},\vec{u}\right)+\left(\vec{u},\vec{OM_{k+1}}\right) \\
&=-\left(\vec{u},\vec{OM_k}\right)+\left(\vec{u},\vec{OM_{k+1}}\right) \\
&=\dfrac{2(k+1)\pi}{n}-\dfrac{2k\pi}{n} \quad [2\pi]\\
&=\dfrac{2\pi}{n} \quad [2\pi]
\end{align*}$

3. Pour $k$ entier tel que $0\leqslant k\leqslant n-1$, démontrer que la longueur de la hauteur issue de $M_{k+1}$ dans le triangle $OM_kM_{k+1}$ est égale à $\left(1+\dfrac{k+1}{n}\right)\times :sin\left(\dfrac{2\pi}{n}\right)$.
On appelle $H$ le pied de la hauteur dans le triangle $OM_kM_{k+1}$.
Le triangle $OHM_{k+1}$ est donc rectangle en $H$.
Ainsi $\sin \widehat{HOM_{k+1}}=\dfrac{HM_{k+1}}{OM_{k+1}}$.
Or $\widehat{HOM_{k+1}}=\widehat{M_kOM_{k+1}}$
Donc $\sin \left(\dfrac{2\pi}{n}\right)=\dfrac{HM_{k+1}}{1+\dfrac{k}{n}}$.
D’où $HM_{k+1}=\left(1+\dfrac{k}{n}\right)\times \sin \left(\dfrac{2\pi}{n}\right)$.
$\quad$
4. On admet que l'aire du triangle $OM_kM_{k+1}$ est égale à $a_k=\dfrac{1}{2}\sin\left(\dfrac{2\pi}{n}\right)\times \left(1+\dfrac{k}{n}\right)\left(1+\dfrac{k+1}{n}\right)$ et que l'aire totale délimitée par la ligne brisée est égale à $A_n+a_0+a_1+\cdots+a_n$.
   L'algorithme suivant permet de calculer l'aire $A_n$ lorsqu'on entre l'entier $n$ : $$\begin{array}{|l |l |} \hline \text{VARIABLES}& A \text{est un nombre réel}\\ & k \text{ est un entier}\\ & n \text{ est un entier}\\ \text{TRAITEMENT}& \text{ Lire la valeur de } n \\ & A \text{ prend la valeur } 0\\ &\text{ Pour } k \text{ allant de 0 à } n-1\\ &\hspace{0,5cm} A \text{ prend la valeur } A+\dfrac{1}{2}\sin\left(\dfrac{2\pi}{n}\right)\times \left(1+\dfrac{k}{n}\right)\left(1+\dfrac{k+1}{n}\right) \\ &\text{Fin Pour }\\ \text{SORTIE }& \text{Afficher } A\\ \hline \end{array} $$
On entre dans l'algorithme $n=10$ Recopier et compléter le tableau ci-dessous qui illustre le fonctionnement de l'algorithme. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline k &0&1&2&3&4&5&6&7&8&9\\ \hline A &0,323&0,711&1,170&10705&2,322&3,027&3,826&4,726& 5,731&6,848 \\ \hline \end{array}$$
5. On admet que $A_2=0$ et que la suite $\left(A_n\right)$ converge et que $\lim_{n\rightarrow +\infty}A_n=\dfrac{7\pi}{3}\approx 7,3$. Recopier et compléter les lignes $L6$ et $L13$ de l'algorithme ci-après qui permet de déterminer le plus petit entier $n$ tel que $A_n\geqslant 7,2$. On ne demande pas de déterminer $n$.
   $$\begin{array}{|l|l|l|}\hline L1 &\text{ VARIABLES }&A \text{ est un nombre réel}\\ L2&&k \text{ est un entier }\\ L3&&n \text{ est un entier}\\ L4& \text{ traitement }&n \text{ prend la valeur 2}\\ L5&&A \text{ prend la valeur } 0\\ L6 &&\text{Tant que}\dots\dots\dots\dots\\ L7&&n \text{ prend la valeur } n+1\\ L8&&A \text{ prend la valeur 0 }\\ L9&& \text{ Pour } k \text{ allant de } 0 \text{ à } n-1\\ L10&&A \text{ prend la valeur } A+\dfrac{1}{2}\sin\left(\dfrac{2\pi}{n}\right)\times \left(1+\dfrac{k}{n}\right)\left(1+\dfrac{k+1}{n}\right)\\ && \text{ Fin Pour }\\ L12&& \text{ Fin Tant que }\\ L13 &\text{SORTIE}&\text{Afficher} \dots\\\hline \end{array}$$
L6 : Tant que $A_n<7,2$
L13 : Afficher $n$
En vidéo !