BAC S 2016 de Mathématiques : Centres Étrangers 8 juin 2016

 

Exercice 1 4 points

Commun à tous les candidats

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse, en justifiant la réponse. il est attribué un point par réponse exacte correctement justifiée. une réponse non justifiée n'est pas prise en compte. une absence de réponse n'est pas pénalisée.

1. Dans une boulangerie industrielle, on prélève au hasard une baguette de pain dans la production. On admet que la variable aléatoie exprimant sa masse, en gramme, suit la loi normale d'espérance 200 et d'écart-type 10.
   Affirmation 1 La probabilité que la masse de la baguette soit supérieure à 187 g est supérieure à 0,9.
2. Affirmation 2 L'équation $x-\cos x=0$ admet une unique solution dans l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$.
   Dans les questions 3. et 4., l'espace est rapporté à un repère orthonormal et l'on considère les droites $\mathscr{D}_1$ et $\mathscr{D}_2$ qui admettent pour rerésentations paramétriques respectives : \[\begin{cases}x=1+2t\\y=2-3t\\z=-4t\end{cases}, t\in\mathbb{R}\hspace{1cm}\text{et}\hspace{1cm}\begin{cases}x=-5t'+3\\y=2t'\\z=t'+4\end{cases}, t'\in\mathbb{R}\]
3. Affirmation 3 Les droites $\mathscr{D}_1$ et $\mathscr{D}_2$ sont sécantes.
4. Affirmation 4 La droite $\mathscr{D}_1$ est parallèle au plan d'équation $x+2y+z-3=0$.

Correction de l'exercice 1 (4 points)

Commun à tous les candidats

 

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse, en justifiant la réponse. il est attribué un point par réponse exacte correctement justifiée. une réponse non justifiée n'est pas prise en compte. une absence de réponse n'est pas pénalisée.

1. Dans une boulangerie industrielle, on prélève au hasard une baguette de pain dans la production. On admet que la variable aléatoie exprimant sa masse, en gramme, suit la loi normale d'espérance 200 et d'écart-type 10.
   Affirmation 1 La probabilité que la masse de la baguette soit supérieure à 187 g est supérieure à 0,9.
Affirmation 1 : Vraie
On calcule :
$\begin{align*} P(X \geqslant 187) &= 0,5 + P(187 \leqslant X \leqslant 200) \\
& \approx 0,903 \\
& > 0,9 \end{align*} $


2ND DISTR 2NORMALFRép( $\1$ , \1,$10^{99}$$\3$)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$

$$P( \5 > \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
 
2. Affirmation 2 L'équation $x-\cos x=0$ admet une unique solution dans l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$.
Affirmation 2 : Vraie
On appelle $f$ la fonction définie sur $I=\left[0;\dfrac{\pi}{2}\right]$ par $f(x)=x-\cos x$.
Cette fonction est dérivable sur $I$ en tant que somme de fonctions dérivables sur $I$.
$f'(x)=1-\cos x \geqslant 0$ car $-1\leqslant \cos x \leqslant 1$ pour tout réel $x$.
La fonction $f$ est donc continue (car dérivable) et strictement croissante sur $I$.
De plus $f(0)=-1<0$ et $f\left(\dfrac{\pi}{2}\right) = \dfrac{\pi}{2}>0$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intérmédiaires) l’équation $f(x)=0$ possède une unique solution.
$\quad$ Dans les questions 3. et 4., l'espace est rapporté à un repère orthonormal et l'on considère les droites $\mathscr{D}_1$ et $\mathscr{D}_2$ qui admettent pour rerésentations paramétriques respectives : \[\begin{cases}x=1+2t\\y=2-3t\\z=-4t\end{cases}, t\in\mathbb{R}\hspace{1cm}\text{et}\hspace{1cm}\begin{cases}x=-5t'+3\\y=2t'\\z=t'+4\end{cases}, t'\in\mathbb{R}\]
3. Affirmation 3 Les droites $\mathscr{D}_1$ et $\mathscr{D}_2$ sont sécantes.
Affirmation 3 : Fausse
Regardons si le système suivant possède un unique couple solution solution :
$\begin{align*} \begin{cases} 1+2t=-5t’+3 \\2-3t=2t’ \\-4t=t’+4 \end{cases} &\iff \begin{cases} 2t=-5t’+2 \\-3t=2t’-2 \\t’=-4t-4 \end{cases} \\
&\iff \begin{cases} 2t=-5(-4t-4)+2 \\-3t=2(-4t-4)-2 \\t’=-4t-4 \end{cases} \\
&\iff \begin{cases} 2t=20t+20+2 \\-3t=-8t-8-2\\t’=4t-4\end{cases} \\
&\iff \begin{cases}-18t=22 \\5t=-10\\t’=-4t-4 \end{cases} \\
&\iff \begin{cases} t=-\dfrac{11}{9}\\t=-2\\t’=-4t-4 \end{cases}
\end{align*}$
Ce système ne possède donc pas de solution.
Les droites ne sont pas sécantes.
$\quad$
4. Affirmation 4 La droite $\mathscr{D}_1$ est parallèle au plan d'équation $x+2y+z-3=0$.
Affirmation 4 : Fausse
Un vecteur directeur de $\mathscr{D}_1$ est $\vec{u}(2;-3;-4)$ et un vecteur normal à $\mathscr{P}$ est $\vec{n}(1;2;1)$.
$\vec{u}.\vec{n}=2-6-4=-8\neq 0$.
Donc la droite $\mathscr{D}_1$ n'est pas parallèle au plan $\mathscr{P}$.
$\quad$ Une autre méthode consiste à déterminer l'intersection de $\mathscr{D}_1$ et $\mathscr{P}$
$\begin{align*}M\in \mathscr{D}_1\cap \mathscr{P} \iff \begin{cases} x=1+2t \\y=2-3t \\z=-4t\\ x+2y+z-3=0 \quad(1) \end{cases} \end{align*}$ $$\begin{align*}(1)\iff& 1+2t+2(2-3t)-4t-3=0\\ \iff& 1+2t+4-6t-4t-3=0\\ \iff& -8t=-2\\ \iff& t= \dfrac{1}{4} \end{align*}$$ En reportant $t= \dfrac{1}{4}$ dans $\begin{cases}x=1+2t\\y=2-3t\\z=-4t\end{cases} $ on obtient $\begin{cases}x=\dfrac{3}{2}\\y=\dfrac{5}{4}\\z=-1\end{cases}$
Ainsi la droite $\mathscr{D}_1$ perce le plan d'équation $x+2y+z-3=0$ en $I\begin{pmatrix} \dfrac{3}{2}\\\dfrac{5}{4}\\ -1 \end{pmatrix}$

Exercice 2 6 points

Commun à tous les candidats

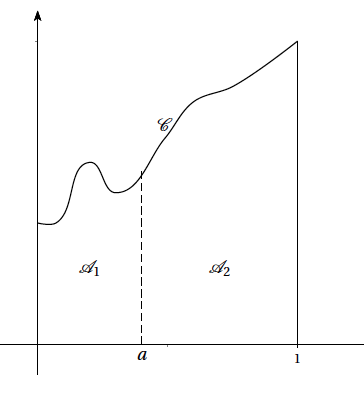
Soit $f$ une fonction définie sur l'intervalle $[0~;~1]$, continue et positive sur cet intervalle, et $a$ une réel tel que $0<a<1$. On note :

$\mathscr{C}$ la courbe représentative de la fonction $f$ dans un repère orthogonal : $\mathscr{A}_1$ l'aire du domaine plan limité par l'axe des abscisses et la courbe $\mathscr{C}$ d'une part, les droites d'équations $x=0$ et $x=a$ d'autre part. $\mathscr{A}_2$ l'aire du domaine plan limité par l'axe des abscisses et la courbe $\mathscr{C}$ d'une part, les droites d'équations $x=a$ et $x=1$ d'autre part.

Figure
Le but de cet exercice est de déterminer, pour différentes fonctions $f$, une valeur du réel $a$ vérifiant la condition (E) : «les aires $\mathscr{A}_1$ et $\mathscr{A}_2$ sont égales». On admet l'existence d'un tel réel $a$ pour chacune des fonctions considérées.

Partie A : Étude de quelques exemples

1. Vérifier que dans les cas suivants, la condition (E) est remplie pour un unique réel $a$ et déterminer sa valeur.
   1. $f$ est une fonction constante strictement positive.
   2. $f$ est définie sur $[0~;~1]$ par $f(x)=x$.
2. 1. À l'aide d'intégrales, exprimer, en unités d'aires, les aires $\mathscr{A}_1$ et $\mathscr{A}_2$.
   2. On note $F$ une primitive de la fonction $f$ sur l'intervalle $[0~;~1]$. Démontrer que si le réel $a$ satisfait la condition (E), alors $F(a)=\dfrac{F(0)+F(1)}{2}$. La réciproque est-elle vraie ?
3. Dans cette question, on envisage deux autres fonctions particulières.
   1. La fonction $f$ est définie pour tout réel $x$ de $[0~;~1]$ par $f(x)=\mathrm{e}^{x}$. Vérifier que la condition (E) est vérifiée pour un unique réel $a$ et donner sa valeur.
   2. La fonction $f$ définie pour tout réel $x$ de $\left[0~;~1\right]$ par $f(x)=\dfrac{1}{(x+2)^2}$. Vérifier que la valeur $a=\dfrac{2}{5}$ convient.

 

Partie B : Utilisation d'une suite pour déterminer une valeur approchée de $a$

Dans cette partie, on considère la fonction $f$ définie pour tout réel $x$ de $[0~;~1]$ par $f(x)=4-3x^2$.

1. Démontrer que si $a$ est un réel satisfaisant la condition (E), alors $a$ est solution de l'équation : \[x=\dfrac{x^3}{4}+\dfrac{3}{8}.\] Dans la suite de l'exercice, on admettra que cette équation a une unique solution dans l'intervalle $[0~;~1]$. on note $\alpha$ cette solution.
2. On considère la fonction $g$ définie pour tout réel $x$ de $[0~;~1]$ par $g(x)=\dfrac{x^3}{4}+\dfrac{3}{8}$ et la suite $\left(u_n\right)$ définie par : $u_0=0$ et, pour tout entier naturel $n$, $u_{n+1}=g\left(u_n\right)$.
   1. Calculer $u_1$.
   2. Démontrer que la fonction $g$ est croissante sur l'intervalle $[0~;~1]$.
   3. Démontrer par récurrence que, pour tout entier naturel $n$, on a $0\leqslant u_n\leqslant u_{n+1}\leqslant 1$.
   4. Prouver que la suite $\left(u_n\right)$ est convergente. À l'aide des opérations sur les limites, prouver que la limite est $a$.
   5. On admet que le réel $a$ vérifie l'inégalité $0 < a-u_{10} < 10^{-9}$. Calculer $u_{10}$ à $10^{-9}$ près.

Correction de l'exercice 2 (6 points)

Commun à tous les candidats

Soit $f$ une fonction définie sur l'intervalle $[0~;~1]$, continue et positive sur cet intervalle, et $a$ une réel tel que $0<a<1$. On note :

$\mathscr{C}$ la courbe représentative de la fonction $f$ dans un repère orthogonal : $\mathscr{A}_1$ l'aire du domaine plan limité par l'axe des abscisses et la courbe $\mathscr{C}$ d'une part, les droites d'équations $x=0$ et $x=a$ d'autre part. $\mathscr{A}_2$ l'aire du domaine plan limité par l'axe des abscisses et la courbe $\mathscr{C}$ d'une part, les droites d'équations $x=a$ et $x=1$ d'autre part.

Figure
Le but de cet exercice est de déterminer, pour différentes fonctions $f$, une valeur du réel $a$ vérifiant la condition (E) : «les aires $\mathscr{A}_1$ et $\mathscr{A}_2$ sont égales». On admet l'existence d'un tel réel $a$ pour chacune des fonctions considérées.

Partie A : Étude de quelques exemples

1. Vérifier que dans les cas suivants, la condition (E) est remplie pour un unique réel $a$ et déterminer sa valeur.
   1. $f$ est une fonction constante strictement positive.
   Si $f$ est constante, il suffit de prendre $a=0,5$.
   $A_1$ et $A_2$ sont les aires de deux rectangles de même longueur et largeur.
   $\quad$
   
   2. $f$ est définie sur $[0~;~1]$ par $f(x)=x$.
   Si $f(x)=x$ sur $[0;1]$.
   On a $A_1=\displaystyle \int_0^a x\mathrm{d}x = \left[\dfrac{x^2}{2}\right]_0^a = \dfrac{a^2}{2}$
   Et $A_2=\displaystyle \int_a^1 x\mathrm{d}x = \left[\dfrac{x^2}{2}\right]_a^1=\dfrac{1-a^2}{2}$.
   On veut donc que $\dfrac{a^2}=\dfrac{1-a^2}{2}$ soit $a^2=1-a^2$ et donc $2a^2=1$ d’où $a^2=\dfrac{1}{2}$.
   Puisque $a>0$ on a alors $a=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}$.
2. 1. À l'aide d'intégrales, exprimer, en unités d'aires, les aires $\mathscr{A}_1$ et $\mathscr{A}_2$.
   On a , puisque la fonction $f$ est continue et positive sur $[0; 1]$ $A_1=\displaystyle \int_0^a f(x)\mathrm{d}x $ et $A_2=\displaystyle \int_a^1 f(x)\mathrm{d}x $.
   $\quad$
   
   2. On note $F$ une primitive de la fonction $f$ sur l'intervalle $[0~;~1]$. Démontrer que si le réel $a$ satisfait la condition (E), alors $F(a)=\dfrac{F(0)+F(1)}{2}$. La réciproque est-elle vraie ?
   Si $F$ est une primitive de $f$ sur $[0;1]$ alors :
   $A_1=F(a)-F(0)$ et $A_2=F(1)-F(a)$.
   $\begin{align*} A_1=A_2 & \iff F(a)-F(0)=F(1)-F(a) \\
   &\iff 2F(a)=F(1)+F(0) \\
   &\iff F(a)=\dfrac{F(1)+F(0)}{2}
   \end{align*}$
   $\quad$
   Il n’y a que des équivalences dans la démarche précédente. La réciproque est donc vraie.
3. Dans cette question, on envisage deux autres fonctions particulières.
   1. La fonction $f$ est définie pour tout réel $x$ de $[0~;~1]$ par $f(x)=\mathrm{e}^{x}$. Vérifier que la condition (E) est vérifiée pour un unique réel $a$ et donner sa valeur.
   Si $f(x)=\text{e}^x$ alors une primitive sur $[0;1]$ est $F$ définie par $F(x)=\text{e}^x$.
   On sait que $F(a)=\dfrac{F(1)+F(0)}{2}$
   On a donc $\text{e}^a=\dfrac{\text{e}^0+\text{e}^1}{2}=\dfrac{1+\text{e}}{2}$.
   Par conséquent $a=\ln \dfrac{1+\text{e}}{2}$.
   $\quad$
   
   2. La fonction $f$ définie pour tout réel $x$ de $\left[0~;~1\right]$ par $f(x)=\dfrac{1}{(x+2)^2}$. Vérifier que la valeur $a=\dfrac{2}{5}$ convient.
   Si $f(x)=\dfrac{1}{(x+2)^2}$ alors une primitive $F$ sur $[0;1]$ est définie par $F(x)=-\dfrac{1}{x+2}$.
   On sait que $F(a)=\dfrac{F(1)+F(0)}{2}$
   Ainsi $\dfrac{1}{a+2}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{2}$
   Donc $\dfrac{1}{a+2}=\dfrac{5}{12}$.
   D’où $5(a+2)=12$.
   Par conséquent $5a+10=12$ et $a=\dfrac{2}{5}$.

 

Partie B : Utilisation d'une suite pour déterminer une valeur approchée de $a$

Dans cette partie, on considère la fonction $f$ définie pour tout réel $x$ de $[0~;~1]$ par $f(x)=4-3x^2$.

1. Démontrer que si $a$ est un réel satisfaisant la condition (E), alors $a$ est solution de l'équation : \[x=\dfrac{x^3}{4}+\dfrac{3}{8}.\] Dans la suite de l'exercice, on admettra que cette équation a une unique solution dans l'intervalle $[0~;~1]$. on note $\alpha$ cette solution.
$f(x)=4-3x^2$
La fonction $F$ définie sur $[0;1]$ par $F(x)=4x-x^3$ est donc une primitive de $f$ sur cet intervalle.
On réutilise la propriété de la question A.2.b.
$4a-a^3=\dfrac{0+(4-1)}{2}$
Soit $4a-a^3=\dfrac{3}{2}$
Donc $8a-2a^3=3$
Ainsi $8a=2a^3+3$
Et par conséquent $a=\dfrac{a^3}{4}+\dfrac{3}{8}$.

2. On considère la fonction $g$ définie pour tout réel $x$ de $[0~;~1]$ par $g(x)=\dfrac{x^3}{4}+\dfrac{3}{8}$ et la suite $\left(u_n\right)$ définie par : $u_0=0$ et, pour tout entier naturel $n$, $u_{n+1}=g\left(u_n\right)$.
   1. Calculer $u_1$.
   $u_1=g(0)=\dfrac{3}{8}$.
   
   2. Démontrer que la fonction $g$ est croissante sur l'intervalle $[0~;~1]$.
   La fonction $g$ est croissante comme somme d’une fonction croissante et d’une fonction constante sur $[0;1]$.
   On peut égaler calculer la dérivée et étudier son signe ....
   3. Démontrer par récurrence que, pour tout entier naturel $n$, on a $0\leqslant u_n\leqslant u_{n+1}\leqslant 1$.
   Initialisation : Si $n=0$.
   Alors $u_0=0$ et $u_1=\dfrac{3}{8}$.
   On a bien $0 \leqslant u_0 \leqslant u_1 \leqslant 1$
   La propriété est donc vraie au rang $0$.
   $\quad$
   Hérédité :On suppose la propriété vraie au rang $n$ : $0\leqslant u_n\leqslant u_{n+1}\leqslant 1$.
   La fonction $g$ est croissante sur l’intervalle $[0;1]$.
   Par conséquent $g(0) \leqslant g\left(u_{n}\right) \leqslant g\left(u_{n+1}\right) \leqslant g(1)$.
   Soit $0 \leqslant \dfrac{3}{8} \leqslant u_{n+1} \leqslant u_{n+2} \leqslant \dfrac{5}{8} \leqslant 1$
   La propriété est donc héréditaire.
   $\quad$
   Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
   Donc pour tout entier naturel $n$ on a : $0\leqslant u_n\leqslant u_{n+1}\leqslant 1$.
   $\quad$
   $\quad$
   
   4. Prouver que la suite $\left(u_n\right)$ est convergente. À l'aide des opérations sur les limites, prouver que la limite est $a$.
   La suite $\left(u_n\right)$ est donc croissante et majorée par $1$; elle converge d'après le théorème de la convergence monotone.
   On appelle $\alpha$ la limite de cette suite.
   Puisque $u_{n+1}=g\left(u_n\right)$ avec $g$ continue sur $\mathbb R$ donc en $\alpha$ cela signifie donc, par passage à la limite, que $\alpha=g(\alpha)$
   et par ailleurs $0\leqslant u_n\leqslant 1$ donc, par passage à la limite, $0\leqslant \alpha \leqslant 1$ .
   Ainsi $\alpha=a$ car d'après l'énoncé l'équation $g(x)=x$ a une unique solution $a$ dans $[0; 1]$.
   $\quad$
   
   5. On admet que le réel $a$ vérifie l'inégalité $0 < a-u_{10} < 10^{-9}$. Calculer $u_{10}$ à $10^{-9}$ près.
   On a, à l’aide de la calculatrice, $u_{10} \approx 0,389~807~84$
   En vidéo !

Exercice 3 5 points

Probabilités

Un institut effectue un sondage pour connaître, dans une population donnée, la proportion de personnes qui soont favorables à un projet d'aménagement du territoire. Pour cela, on interroge un échantillon aléatoire de personnes de cette population, et l'on pose une question à chaque personne.
Les trois parties sont relatives à cette même situation, mais peuvent être traitées de manière indépendante.

Partie A : Nombre de personnes qui acceptent de répondre au sondage

On admet dans cette partie ue la probabilité qu'une personne interrogée accepte de répondre à la question est égale à 0,6.

1. L'institut de sondage interroge 700 personnes. On note $X$ la variable aléatoire correspondant au nombre de personnes interrogées qui acceptent de répondre à la question posée.
   1. Quelle est la loi de la variable aléatoire $X$ ? Justifier la réponse.
   2. Quelle est la meilleure approximation de $P(X\geqslant 400)$ parmi les nombres suivants ? \[0,92\hspace{2cm} 0,93\hspace{2cm}0,94\hspace{2cm}0,95.\]
2. Combien de personnes l'institut doit-il interroger au minimum pour garantir, avec une probabilité supérieur à 0,9, que le nombre de personnes répondant au sondage soit supérieur ou égal à 400.

 

Partie B : Proportion de personnes favorables au projet dans la population

Dans cette partie, on suppose que $n$ personnes ont répondu à la question ,et on admet que ces personnes constituent un échantillon aléatoire de taille $n$ (où $n$ est un entier naturel supérieur à 50). Parmi ces personnes, 29% sont favorables au projet d'aménagement.

1. Donner un intervalle de confiance, au niveau de confiance de 95%, de la proportion de personnes qui sont favorables au projet dans la population totale.
2. Déterminer la valeur minimale de l'entier $n$ pour que l'intervalle de confiance, au niveau de confiance de 95%, ait une amplitude inférieure ou égale à 0,04.

 

Partie C : Correction dûe à l'insincérité de certaines réponses

Dans cette partie, on suppose que, parmi les personnes sondées qui ont accepté de répondre à la question posée, 29% affirment qu'elles sont favorables au projet. L'institut de sondage sait par ailleurs que la question posée pouvant être gênante pour les personnes interrogées, certaines d'entre elles ne sont pas sincères et répondent le contraire de leur opinion véritable. Ainsi, une personne qui se dit favorable peut :

• soit être en réalité favorable au projet si elle est sincère.
• soit être en réalité défavorable au projet si elle n'est pas sincère.

Par expérience, l'institut estime à 15% le taux de réponses non sincères parmi les personnes ayant répondu, et admet que ce taux est le même quelle que soit l'opinion de la personne interrogée. Le but de cette partie est, à partir de ces données, de déterminer le taux réel de personnes favorables au projet, à l'aide d 'un modèle probabiliste. on prélève au hasard la fiche d'une personne ayant répondu, et on définit :

• $F$ l'événement «la personne est en réalité favorable au projet» ;
• $\overline{F}$ l'événement «la personne est en réalité défavorable au projet» ;
• $A$ l'événement «la personne affirme qu'elle est favorablee au projet»;
• $\overline{A}$ l'événement «la personne affirme qu'elle est défavorable au projet».

Ainsi, d'après les données, on a $p(A)=0,29$.

1. En interprétant les données de l'énoncé, indiquer les valeurs de $P_F(A)$ et $P_{\overline{F}}(A)$.
2. 
   

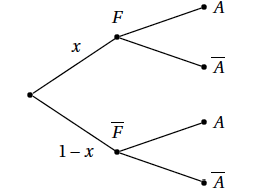
   On pose $x=P(F)$. Reproduire sur la copie et compléter l'arbre de probabilité ci-contre. En déduire une égalité vérifiée par $x$

3. Déterminer, parmi les personnes ayant répondu au sondage, la proportion de celles qui sont réellement favorables au projet.

 

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Un institut effectue un sondage pour connaître, dans une population donnée, la proportion de personnes qui soont favorables à un projet d'aménagement du territoire. Pour cela, on interroge un échantillon aléatoire de personnes de cette population, et l'on pose une question à chaque personne.
Les trois parties sont relatives à cette même situation, mais peuvent être traitées de manière indépendante.

Partie A : Nombre de personnes qui acceptent de répondre au sondage

On admet dans cette partie ue la probabilité qu'une personne interrogée accepte de répondre à la question est égale à 0,6.

1. L'institut de sondage interroge 700 personnes. On note $X$ la variable aléatoire correspondant au nombre de personnes interrogées qui acceptent de répondre à la question posée.
   1. Quelle est la loi de la variable aléatoire $X$ ? Justifier la réponse.
   
   

   On répète $\1$  fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :

   • « \3 » considéré comme succès, de probabilité $p=\4$
   • « \5 » considéré comme échec, de probabilité $q=1-p=\6$

   Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$  et $\4$ notée $\mathscr{B}(\1;\4)$ .

   Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$

   2. Quelle est la meilleure approximation de $P(X\geqslant 400)$ parmi les nombres suivants ? \[0,92\hspace{2cm} 0,93\hspace{2cm}0,94\hspace{2cm}0,95.\]
   $P(X \geqslant 400) = 1-P(X \leqslant 399) \approx 0,94$.
   

    

   2ND DISTR AbinomFRép( \1 , \2,\3)EXE
   Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$

   $$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
   Donc $P(X \geqslant 400) = 1-P(X \leqslant 399) \approx 0,943$
   En vidéo !
2. Combien de personnes l'institut doit-il interroger au minimum pour garantir, avec une probabilité supérieur à 0,9, que le nombre de personnes répondant au sondage soit supérieur ou égal à 400.
On appelle $X’$ la variable aléatoire qui compte le nombre de personne acceptant de répondre à la question parmi $n$ personnes.
$X’$ suit la loi binomiale de paramètres $n$ et $p=0,6$.
On veut que $P(X’ \leqslant 400) > 0,9$.
Si $n=693$ alors $P(X’ \leqslant 400) \approx 0,896~6$
Si $n=694$ alors $P(X’ \leqslant 400) \approx 0,904~5$


 

2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$

$$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$

Donc $P(X’ \leqslant 400) \approx 1-P(X'\leq 399)\approx0,897$

 

2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$

$$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$

Donc $P(X’ \leqslant 400) \approx 1-P(X'\leq 399)\approx0,905$
Il faut donc interroger $694$ personnes.

 

Partie B : Proportion de personnes favorables au projet dans la population

Dans cette partie, on suppose que $n$ personnes ont répondu à la question ,et on admet que ces personnes constituent un échantillon aléatoire de taille $n$ (où $n$ est un entier naturel supérieur à 50). Parmi ces personnes, 29% sont favorables au projet d'aménagement.

1. Donner un intervalle de confiance, au niveau de confiance de 95%, de la proportion de personnes qui sont favorables au projet dans la population totale.

La fréquence est égale à  $0,29$. La taille de l'échantillon considéré est égale à $n$
Comme  $ n \geq 50$ ,   $n \times f  =14,5$  et $n\times (1-f)=35,5$ les conditions d'utilisation d'un intervalle de confiance sont réunies.

En effet on a bien : $$n \geq 30\;;\; n \times f \geq 5 \text{ et } n\times (1-f) \geq 5$$

L' intervalle de confiance avec un niveau de confiance de 95% est : \[I = \left[f - \dfrac{1}{\sqrt{n}}~;~f +\dfrac{1}{\sqrt{n}} \right]\]
La fréquence est $f=0,29$.


L'intervalle de confiance au niveau de 95% est $$I_n = \left[0,29 - \dfrac{1}{\sqrt{n}}~;~0,29 + \dfrac{1}{\sqrt{n}} \right] $$

2. Déterminer la valeur minimale de l'entier $n$ pour que l'intervalle de confiance, au niveau de confiance de 95%, ait une amplitude inférieure ou égale à 0,04.
L’amplitude de cet intervalle est donc $\dfrac{2}{\sqrt{n}}$.
On veut ainsi que $\dfrac{2}{\sqrt{n}} \leqslant 0,04$
Soit $\dfrac{2}{0,04}\leqslant \sqrt{n}$
C’est-à-dire $50 \leqslant \sqrt{n}$ et donc $n \geqslant 2~500$.

 

Partie C : Correction dûe à l'insincérité de certaines réponses

Dans cette partie, on suppose que, parmi les personnes sondées qui ont accepté de répondre à la question posée, 29% affirment qu'elles sont favorables au projet. L'institut de sondage sait par ailleurs que la question posée pouvant être gênante pour les personnes interrogées, certaines d'entre elles ne sont pas sincères et répondent le contraire de leur opinion véritable. Ainsi, une personne qui se dit favorable peut :

• soit être en réalité favorable au projet si elle est sincère.
• soit être en réalité défavorable au projet si elle n'est pas sincère.

Par expérience, l'institut estime à 15% le taux de réponses non sincères parmi les personnes ayant répondu, et admet que ce taux est le même quelle que soit l'opinion de la personne interrogée. Le but de cette partie est, à partir de ces données, de déterminer le taux réel de personnes favorables au projet, à l'aide d 'un modèle probabiliste. on prélève au hasard la fiche d'une personne ayant répondu, et on définit :

• $F$ l'événement «la personne est en réalité favorable au projet» ;
• $\overline{F}$ l'événement «la personne est en réalité défavorable au projet» ;
• $A$ l'événement «la personne affirme qu'elle est favorablee au projet»;
• $\overline{A}$ l'événement «la personne affirme qu'elle est défavorable au projet».

Ainsi, d'après les données, on a $p(A)=0,29$.

1. En interprétant les données de l'énoncé, indiquer les valeurs de $P_F(A)$ et $P_{\overline{F}}(A)$.
$P_F(A) = 1-0,15=0,85$.
Et $P_{\overline{F}}(A)=0,15$ puisque le taux ne change pas en fonction de l’opinion.

2. 
   

   On pose $x=P(F)$. Reproduire sur la copie et compléter l'arbre de probabilité ci-contre. En déduire une égalité vérifiée par $x$ D’après la formule des probabilités totales on a : $\begin{align*} P(A)=P(F\cap A)+P\left(\overline{F}\cap A\right) &\iff 0,29 = 0,85x+0,15(1-x) \\ &\iff 0,29 = 0,85x+0,15-0,15x \\ &\iff 0,14=0,7x \\ &\iff x = \dfrac{0,14}{0,7} \\ &\iff x= 0,2 \end{align*}$ $\quad$ Remarque : on ne demandait à cette question qu’une égalité et non la solution de l’équation !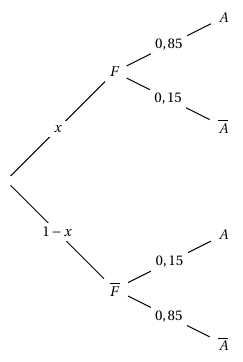

3. Déterminer, parmi les personnes ayant répondu au sondage, la proportion de celles qui sont réellement favorables au projet.
On veut calculer $P(F)=0,2$
Donc $20\%$ des personnes sont réellement favorable au projet.

 

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On veut modéliser dans le plan la coquille d'un nautile à l'aide d'une ligne brisée en forme de spirale. on s'intéresse à l'aire délimitée par cette ligne.
On munit le ;plan d'un repère orthormal direct $\left(O~;~\overrightarrow{u}~;~\overrightarrow{v}\right)$. Soit $n$ un entier supérieur ou égal à 2. Pour tout entier $k$ allant de 0 à $n$, on définit les nombres complexes $z_k=\left(1+\dfrac{k}{n}\right)\mathrm{e}^{\mathrm{i}\frac{2k\pi}{n}}$ et on note $M_k$ le point d'affixe $z_k$. Dans ce modèle, le pourtour du nautile est la ligne visée reliant tous les points $M_k$ avec $0\leqslant k\leqslant n$. Par exemple, pour les entiers $n=6$, $n=10$ et $n=20$, on obtient les figures ci-dessous.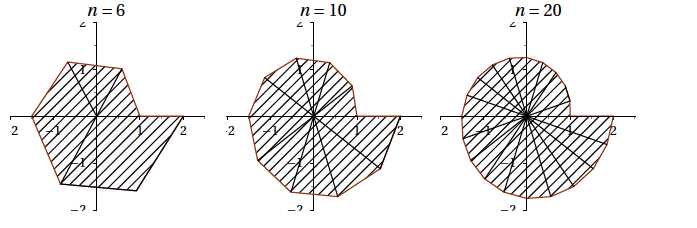

Partie A : Ligne brisée formée à partir de sept points

Dans cette partie, on suppose que $n=6$. Ainsi, pour $0\leqslant k\leqslant 6$, on a $z_k=\left(1+\dfrac{k}{6}\right)\mathrm{e}^{\mathrm{i}\frac{2k\pi}{6}}$.

1. Déterminer la forme algébrique de $z_1$.
2. Vérifier que $z_0$ et $z_6$ sont des entiers que l'on déterminera.
3. Calculer la longueur de la hauteur issue de $M_1$ dans le triangle $OM_0M_1$ puis établir que l'aire de ce triangle est égale à $\dfrac{7\sqrt{3}}{24}$.

 

Partie B : Ligne brisée formée à partir de $n+1$ points

Dans cette partie, $n$ est un entier supérieur ou égal à 2.

1. Pour tout entier $k$ tel que $0\leqslant k\leqslant n$, déterminer la longueur $OM_k$.
2. Pour $k$ entier tel que $0\leqslant k\leqslant n-1$, déterminer une mesure des angles $\left(\overrightarrow{\text{u}}~;~\overrightarrow{OM_k}\right)$ et $\left(\overrightarrow{\text{u}}~;~\overrightarrow{OM_{k+1}}\right)$. En déduire une mesure de l'angle $\left(\overrightarrow{OM_k}~;~\overrightarrow{OM_{k+1}}\right)$.
3. Pour $k$ entier tel que $0\leqslant k\leqslant n-1$, démontrer que la longueur de la hauteur issue de $M_{k+1}$ dans le triangle $OM_kM_{k+1}$ est égale à $\left(1+\dfrac{k+1}{n}\right)\times :sin\left(\dfrac{2\pi}{n}\right)$.
4. On admet que l'aire du triangle $OM_kM_{k+1}$ est égale à $a_k=\dfrac{1}{2}\sin\left(\dfrac{2\pi}{n}\right)\times \left(1+\dfrac{k}{n}\right)\left(1+\dfrac{k+1}{n}\right)$ et que l'aire totale délimitée par la ligne brisée est égale à $A_n+a_0+a_1+\cdots+a_n$.
   L'algorithme suivant permet de calculer l'aire $A_n$ lorsqu'on entre l'entier $n$ : $$\begin{array}{|l |l |} \hline \text{VARIABLES}& A \text{est un nombre réel}\\ & k \text{ est un entier}\\ & n \text{ est un entier}\\ \text{TRAITEMENT}& \text{ Lire la valeur de } n \\ & A \text{ prend la valeur } 0\\ &\text{ Pour } k \text{ allant de 0 à } n-1\\ &\hspace{0,5cm} A \text{ prend la valeur } A+\dfrac{1}{2}\sin\left(\dfrac{2\pi}{n}\right)\times \left(1+\dfrac{k}{n}\right)\left(1+\dfrac{k+1}{n}\right) \\ &\text{Fin Pour }\\ \text{SORTIE }& \text{Afficher } A\\ \hline \end{array} $$
On entre dans l'algorithme $n=10$ Recopier et compléter le tableau ci-dessous qui illustre le fonctionnement de l'algorithme. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline k &0&1&2&3&4&5&6&7&8&9\\ \hline A &0,323&0,711&1,170&10705&2,322&3,027&3,826&4,726&&\\ \hline \end{array}$$
5. On admet que $A_2=0$ et que la suite $\left(A_n\right)$ converge et que $\lim_{n\rightarrow +\infty}A_n=\dfrac{7\pi}{3}\approx 7,3$. Recopier et compléter les lignes $L6$ et $L13$ de l'algorithme ci-après qui permet de déterminer le plus petit entier $n$ tel que $A_n\geqslant 7,2$. On ne demande pas de déterminer $n$.
   $$\begin{array}{|l|l|l|}\hline L1 &\text{ VARIABLES }&A \text{ est un nombre réel}\\ L2&&k \text{ est un entier }\\ L3&&n \text{ est un entier}\\ L4& \text{ traitement }&n \text{ prend la valeur 2}\\ L5&&A \text{ prend la valeur } 0\\ L6 &&\text{Tant que}\dots\dots\dots\dots\\ L7&&n \text{ prend la valeur } n+1\\ L8&&A \text{ prend la valeur 0 }\\ L9&& \text{ Pour } k \text{ allant de } 0 \text{ à } n-1\\ L10&&A \text{ prend la valeur } A+\dfrac{1}{2}\sin\left(\dfrac{2\pi}{n}\right)\times \left(1+\dfrac{k}{n}\right)\left(1+\dfrac{k+1}{n}\right)\\ && \text{ Fin Pour }\\ L12&& \text{ Fin Tant que }\\ L13 &\text{SORTIE}&\text{Afficher} \dots\\\hline \end{array}$$

 

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On veut modéliser dans le plan la coquille d'un nautile à l'aide d'une ligne brisée en forme de spirale. on s'intéresse à l'aire délimitée par cette ligne.
On munit le ;plan d'un repère orthormal direct $\left(O~;~\overrightarrow{u}~;~\overrightarrow{v}\right)$. Soit $n$ un entier supérieur ou égal à 2. Pour tout entier $k$ allant de 0 à $n$, on définit les nombres complexes $z_k=\left(1+\dfrac{k}{n}\right)\mathrm{e}^{\mathrm{i}\frac{2k\pi}{n}}$ et on note $M_k$ le point d'affixe $z_k$. Dans ce modèle, le pourtour du nautile est la ligne visée reliant tous les points $M_k$ avec $0\leqslant k\leqslant n$. Par exemple, pour les entiers $n=6$, $n=10$ et $n=20$, on obtient les figures ci-dessous.

Partie A : Ligne brisée formée à partir de sept points

Dans cette partie, on suppose que $n=6$. Ainsi, pour $0\leqslant k\leqslant 6$, on a $z_k=\left(1+\dfrac{k}{6}\right)\mathrm{e}^{\mathrm{i}\frac{2k\pi}{6}}$.

1. Déterminer la forme algébrique de $z_1$.
$z_1=\left(1+\dfrac{1}{6}\right)\text{e}^{\text{i}\pi/3} = \dfrac{7}{6}\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\text{i}\right)$
Donc $z_1=\dfrac{7}{12}+\dfrac{7\sqrt{3}}{12}\text{i}$
$\quad$
2. Vérifier que $z_0$ et $z_6$ sont des entiers que l'on déterminera.
$z_0=1\text{e}^0\text{i} = 1$ est bien un entier.
$z_6=2\text{e}^{12\text{i}\pi/6}=2\text{e}^{2\text{i}\pi} = 2$ est également un entier.

3. Calculer la longueur de la hauteur issue de $M_1$ dans le triangle $OM_0M_1$ puis établir que l'aire de ce triangle est égale à $\dfrac{7\sqrt{3}}{24}$.
La hauteur issur de $M_1$ dans le triangle $OM_0M_1$ correspond à la partie imaginaire de $z_1$. Elle mesure donc $\dfrac{7\sqrt{3}}{12}$.
L’aire de ce triangle vaut ainsi $\dfrac{\dfrac{7\sqrt{3}}{12} \times 1}{2}=\dfrac{7\sqrt{3}}{24}$.
$\quad$

 

Partie B : Ligne brisée formée à partir de $n+1$ points

Dans cette partie, $n$ est un entier supérieur ou égal à 2.

1. Pour tout entier $k$ tel que $0\leqslant k\leqslant n$, déterminer la longueur $OM_k$.
$OM_k=\left|z_k\right|=1+\dfrac{k}{n}$ pour tout entier $k$ tel que $0\leqslant k\leqslant n$.

2. Pour $k$ entier tel que $0\leqslant k\leqslant n-1$, déterminer une mesure des angles $\left(\overrightarrow{\text{u}}~;~\overrightarrow{OM_k}\right)$ et $\left(\overrightarrow{\text{u}}~;~\overrightarrow{OM_{k+1}}\right)$. En déduire une mesure de l'angle $\left(\overrightarrow{OM_k}~;~\overrightarrow{OM_{k+1}}\right)$.
$\left(\vec{u},\vec{OM_k}\right) = \arg\left(z_k\right) = \dfrac{2k\pi}{n}$ modulo $2\pi$ .
$\left(\vec{u},\vec{OM_{k+1}}\right) = \arg\left(z_{k+1}\right) = \dfrac{2(k+1)\pi}{n}$ modulo $2\pi$.
$\quad$
$\begin{align*} \left(\vec{OM_k},\vec{OM_{k+1}}\right)&= \left(\vec{OM_k},\vec{u}\right)+\left(\vec{u},\vec{OM_{k+1}}\right) \\
&=-\left(\vec{u},\vec{OM_k}\right)+\left(\vec{u},\vec{OM_{k+1}}\right) \\
&=\dfrac{2(k+1)\pi}{n}-\dfrac{2k\pi}{n} \quad [2\pi]\\
&=\dfrac{2\pi}{n} \quad [2\pi]
\end{align*}$

3. Pour $k$ entier tel que $0\leqslant k\leqslant n-1$, démontrer que la longueur de la hauteur issue de $M_{k+1}$ dans le triangle $OM_kM_{k+1}$ est égale à $\left(1+\dfrac{k+1}{n}\right)\times :sin\left(\dfrac{2\pi}{n}\right)$.
On appelle $H$ le pied de la hauteur dans le triangle $OM_kM_{k+1}$.
Le triangle $OHM_{k+1}$ est donc rectangle en $H$.
Ainsi $\sin \widehat{HOM_{k+1}}=\dfrac{HM_{k+1}}{OM_{k+1}}$.
Or $\widehat{HOM_{k+1}}=\widehat{M_kOM_{k+1}}$
Donc $\sin \left(\dfrac{2\pi}{n}\right)=\dfrac{HM_{k+1}}{1+\dfrac{k}{n}}$.
D’où $HM_{k+1}=\left(1+\dfrac{k}{n}\right)\times \sin \left(\dfrac{2\pi}{n}\right)$.
$\quad$
4. On admet que l'aire du triangle $OM_kM_{k+1}$ est égale à $a_k=\dfrac{1}{2}\sin\left(\dfrac{2\pi}{n}\right)\times \left(1+\dfrac{k}{n}\right)\left(1+\dfrac{k+1}{n}\right)$ et que l'aire totale délimitée par la ligne brisée est égale à $A_n+a_0+a_1+\cdots+a_n$.
   L'algorithme suivant permet de calculer l'aire $A_n$ lorsqu'on entre l'entier $n$ : $$\begin{array}{|l |l |} \hline \text{VARIABLES}& A \text{est un nombre réel}\\ & k \text{ est un entier}\\ & n \text{ est un entier}\\ \text{TRAITEMENT}& \text{ Lire la valeur de } n \\ & A \text{ prend la valeur } 0\\ &\text{ Pour } k \text{ allant de 0 à } n-1\\ &\hspace{0,5cm} A \text{ prend la valeur } A+\dfrac{1}{2}\sin\left(\dfrac{2\pi}{n}\right)\times \left(1+\dfrac{k}{n}\right)\left(1+\dfrac{k+1}{n}\right) \\ &\text{Fin Pour }\\ \text{SORTIE }& \text{Afficher } A\\ \hline \end{array} $$
On entre dans l'algorithme $n=10$ Recopier et compléter le tableau ci-dessous qui illustre le fonctionnement de l'algorithme. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline k &0&1&2&3&4&5&6&7&8&9\\ \hline A &0,323&0,711&1,170&10705&2,322&3,027&3,826&4,726& 5,731&6,848 \\ \hline \end{array}$$
5. On admet que $A_2=0$ et que la suite $\left(A_n\right)$ converge et que $\lim_{n\rightarrow +\infty}A_n=\dfrac{7\pi}{3}\approx 7,3$. Recopier et compléter les lignes $L6$ et $L13$ de l'algorithme ci-après qui permet de déterminer le plus petit entier $n$ tel que $A_n\geqslant 7,2$. On ne demande pas de déterminer $n$.
   $$\begin{array}{|l|l|l|}\hline L1 &\text{ VARIABLES }&A \text{ est un nombre réel}\\ L2&&k \text{ est un entier }\\ L3&&n \text{ est un entier}\\ L4& \text{ traitement }&n \text{ prend la valeur 2}\\ L5&&A \text{ prend la valeur } 0\\ L6 &&\text{Tant que}\dots\dots\dots\dots\\ L7&&n \text{ prend la valeur } n+1\\ L8&&A \text{ prend la valeur 0 }\\ L9&& \text{ Pour } k \text{ allant de } 0 \text{ à } n-1\\ L10&&A \text{ prend la valeur } A+\dfrac{1}{2}\sin\left(\dfrac{2\pi}{n}\right)\times \left(1+\dfrac{k}{n}\right)\left(1+\dfrac{k+1}{n}\right)\\ && \text{ Fin Pour }\\ L12&& \text{ Fin Tant que }\\ L13 &\text{SORTIE}&\text{Afficher} \dots\\\hline \end{array}$$
L6 : Tant que $A_n<7,2$
L13 : Afficher $n$
En vidéo !

 

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Le but de cet exercice est d'étudier, sur un exemple, une méthode de chiffrement publiée en 1929 par le mathématicien et cryptologue Lester Hill. Ce chiffrement repose sur la donnée d'une matrice $A$, connue uniquement de l'émetteur et du destinataire. Dans tout l'exercice, on note $A$ la matrice définie par : $A = \begin{pmatrix}5&2\\7&7\end{pmatrix}$.

Partie A -- Chiffrement de Hill

Voici les différentes étapes de chiffrement pour un mot comportant un nombre pair de lettres : $$\begin{array} {|l|l|}\hline \text{ Étape 1 }&\text{ On divise le mot en blocs de deux lettres consécutives puis, pour chaque bloc, on effectue chacune des étapes suivantes.}\\ \hline \text{ Étape 2}&\text{ On associe aux deux lettres du bloc les deux entiers } x_1 \text{ et } x_2 \text{tous deux compris entre 0 et 25, qui correspondent aux deux lettres dans le même ordre, dans le tableau suivant :}\\ & \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline A &B &C &D &E &F &G &H &I &J &K &L &M\\ \hline 0 &1 &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12\\ \hline\hline N &O &P &Q &R &S &T &U &V &W &X &Y &Z\\ \hline 13 &14 &15 &16 &17 &18 &19 &20 &21 &22 &23 &24 &25\\ \hline \end{array} \\ \hline \text{Étape 3 }& \text{On transforme la matrice } X = \begin{pmatrix}x_1\\x_2\end{pmatrix} \text{ en la matrice } Y = \begin{pmatrix}y_1\\y_2\end{pmatrix} \text{ vérifiant } Y = A X .\\ \hline \text{Étape 4 }&\text{On transforme la matrice } Y = \begin{pmatrix}y_1\\y_2\end{pmatrix} \text{ en la matrice } R = \begin{pmatrix}r_1\\r_2\end{pmatrix} \text{, où } r_1 \text{ est le reste de la division euclidienne de } y_1 \text{ par 26 et} r_2 \text{ celui de la division euclidienne de } y_2 \text{ par } 26.\\ \hline \text{Étape 5 }&\text{ On associe aux entiers } r_1 \text{ et } r_2 \text{ les deux lettres correspondantes du tableau de l'étape 2. }\\ &\text{ Le bloc chiffré est le bloc obtenu en juxtaposant ces deux lettres.}\\ \hline \end{array} $$
Question : utiliser la méthode de chiffrement exposée pour chiffrer le mot « HILL ».

Partie B - Quelques outils mathématiques nécessaires au déchiffrement

 

1. Soit $a$ un entier relatif premier avec 26. Démontrer qu'il existe un entier relatif $u$ tel que $u \times a \equiv 1 \:\text{modulo}\: 26$.
2. On considère l'algorithme suivant : $$ \begin{array}{|c|lX|}\hline \text{VARIABLES :} & a, u , \text{ et } r \text{ sont des nombres ( } a \text{ est naturel et premier avec 26)}\\ \text{TRAITEMENT :}& \text{Lire } a \\ & u \text{ prend la valeur 0, et } r \text{ prend la valeur 0 } \\ &\text{Tant que } r \neq 1 \\ &\hspace{0,8cm} u \text{ prend la valeur }u + 1\\ & \hspace{0,8cm}r \text{ prend la valeur du reste de la division euclidienne de } u \times a \text{ par } 26 \\ &\text{ Fin du Tant que } \\ \text{ SORTIE } &\text{Afficher } u \\ \hline \end{array}$$
On entre la valeur $ a = 21$ dans cet algorithme.
3. 1. Reproduire et compléter le tableau suivant jusqu’à l’arrêt de l’algorithme.
   2. En déduire que $5 \times 21 \equiv 1 \:\text{modulo}\: 26$
4. On rappelle que $A = \begin{pmatrix}5&2\\7&7\end{pmatrix}$ et on note $I = Id_2 = \begin{pmatrix}1&0\\0&1\end{pmatrix}$
   1. Calculer la matrice $12A - A^2$.
   2. En déduire la matrice $B$ telle que $BA = 21I$.
   3. Démontrer que si $AX = Y$ alors $21X = BY$ .

Partie C : Déchiffrement

On veut déchiffrer le mot V LUP.

On note $X = \begin{pmatrix}x_1\\x_2\end{pmatrix}$ la matrice associée, selon le tableau de correspondance, à un bloc de deux lettres avant chiffrement, et $Y = \begin{pmatrix}y_1\\y_2\end{pmatrix}$ la matrice définie par l'égalité : $Y = A X = \begin{pmatrix}5&2\\7&7\end{pmatrix}X$.
Si $r_1$ et $r_2$ sont les restes respectifs de $y_1$ et $y_2$ dans la division euclidienne par 26, le bloc de deux lettres après chiffrement est associé à la matrice $R = \begin{pmatrix}r_1\\r_2\end{pmatrix}$.

1. Démontrer que : $\left\{\begin{array}{l c l} 21x_1 &=& \phantom{-}7y_1 - 2y_2\\ 21x_2 &=&- 7y_1 + 5 y_2 \end{array}\right.$
2. En utilisant la question B .2., établir que: $\left\{\begin{array}{l c l r} x_1 &\equiv&9r_1 + 16r_2 \:\:&\text{modulo}\: 26\\ x_2 &\equiv&17r_1 + 25r_2 \:\:&\text{modulo}\: 26 \end{array}\right.$
3. Déchiffrer le mot VLUP, associé aux matrices $\begin{pmatrix}21\\11\end{pmatrix}$ et $\begin{pmatrix}20\\15\end{pmatrix}$.

Correction de l'exercice de Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

On décompose HILL en HI et LL
Ainsi dans un premier temps $X=\begin{pmatrix}7\\8\end{pmatrix}$
$Y=AX=\begin{pmatrix}51\\105\end{pmatrix}$
Or $51\equiv 25\quad [26]$ et $105\equiv 1 \quad [26]$.
Donc HI est codé par ZB
$\quad$
On prend maintenant le couple de lettre LL $X=\begin{pmatrix}11\\11\end{pmatrix}$
$Y=AX=\begin{pmatrix}77\\154\end{pmatrix}$
Or $77\equiv 25\quad [26]$ et $154\equiv 24 \quad [26]$.
Donc HI est codé par ZY

Donc HILL est codé par ZBZY
$\quad$

Partie B - Quelques outils mathématiques nécessaires au déchiffrement

 

1. Soit $a$ un entier relatif premier avec 26. Démontrer qu'il existe un entier relatif $u$ tel que $u \times a \equiv 1 \:\text{modulo}\: 26$.
$a$ et $26$ sont premiers entre eux.
D’après le théorème de Bézout il existe donc deux entiers relatifs $u$ et $v$ tels que
$u\times a+26 \times v=1$
En passant au modulo $26$ on a alors $v \times 26\equiv 1\quad [26]$.

2. On considère l'algorithme suivant : $$ \begin{array}{|c|lX|}\hline \text{VARIABLES :} & a, u , \text{ et } r \text{ sont des nombres ( } a \text{ est naturel et premier avec 26)}\\ \text{TRAITEMENT :}& \text{Lire } a \\ & u \text{ prend la valeur 0, et } r \text{ prend la valeur 0 } \\ &\text{Tant que } r \neq 1 \\ &\hspace{0,8cm} u \text{ prend la valeur }u + 1\\ & \hspace{0,8cm}r \text{ prend la valeur du reste de la division euclidienne de } u \times a \text{ par } 26 \\ &\text{ Fin du Tant que } \\ \text{ SORTIE } &\text{Afficher } u \\ \hline \end{array}$$
3. 1. Reproduire et compléter le tableau suivant jusqu’à l’arrêt de l’algorithme.
   $$\begin{array}{|c|c|c|c|c|c|c|}
   \hline
   u&0&1&2&3&4&5 \\
   \hline
   r&0&21&16&11&6&1\\
   \hline
   \end{array}$$
   L’algorithme permet de fournir un entier naturel $u$ tel que $u\times a \equiv 1\quad [26]$
   
   2. En déduire que $5 \times 21 \equiv 1 \:\text{modulo}\: 26$
   L’algorithme affiche $5$ pour $a=21$ donc $5\times 21 \times 5 \equiv 1\quad [26]$.
4. On rappelle que $A = \begin{pmatrix}5&2\\7&7\end{pmatrix}$ et on note $I = Id_2 = \begin{pmatrix}1&0\\0&1\end{pmatrix}$
   1. Calculer la matrice $12A - A^2$.
   $12A=\begin{pmatrix} 60&24\\84&84\end{pmatrix}$
   $A^2=\begin{pmatrix} 39&24\\84&63\end{pmatrix}$
   Donc $12A-A^2=\begin{pmatrix}21&0\\0&21\end{pmatrix}$
   Soit $12A-A^2=21I$.
   
   2. En déduire la matrice $B$ telle que $BA = 21I$.
   $12A-A^2=21I \iff (12I-A)\times A =21I$
   Donc $B=12I-A$.
   $\quad$
   
   3. Démontrer que si $AX = Y$ alors $21X = BY$ .
   Si $AX=Y$ alors $BAX=BY$ soit $21IA=BY$ et donc $21X=BY$.
   $\quad$

Partie C : Déchiffrement

On veut déchiffrer le mot VLUP.

On note $X = \begin{pmatrix}x_1\\x_2\end{pmatrix}$ la matrice associée, selon le tableau de correspondance, à un bloc de deux lettres avant chiffrement, et $Y = \begin{pmatrix}y_1\\y_2\end{pmatrix}$ la matrice définie par l'égalité : $Y = A X = \begin{pmatrix}5&2\\7&7\end{pmatrix}X$.
Si $r_1$ et $r_2$ sont les restes respectifs de $y_1$ et $y_2$ dans la division euclidienne par 26, le bloc de deux lettres après chiffrement est associé à la matrice $R = \begin{pmatrix}r_1\\r_2\end{pmatrix}$.

1. Démontrer que : $\left\{\begin{array}{l c l} 21x_1 &=& \phantom{-}7y_1 - 2y_2\\ 21x_2 &=&- 7y_1 + 5 y_2 \end{array}\right.$
$B=12I-A=\begin{pmatrix} 7&-2\\-7&5\end{pmatrix}$
Donc $21X=BY \iff \begin{cases} 21x_1=7y_1-2y_2 \\21x_2=-7y_1+5y_2\end{cases}$
$\quad$
2. En utilisant la question B .2., établir que: $\left\{\begin{array}{l c l r} x_1 &\equiv&9r_1 + 16r_2 \:\:&\text{modulo}\: 26\\ x_2 &\equiv&17r_1 + 25r_2 \:\:&\text{modulo}\: 26 \end{array}\right.$
On multiplie les deux lignes de ce système par $5$.
$\begin{cases} 5\times 21x_1=35y_1-10y_2\\5\times 21x_2=-35y_1+25y_2\end{cases}$
On passe au modulo $26$ et on utilise le fait que $5\times 21 \equiv 1 \quad[26]$
Donc $\begin{cases} x_1\equiv 9r_1+16r_2 \quad [26] \\x_2=17r_1+25r_2 \quad [26] \end{cases}$
$\quad$
3. Déchiffrer le mot VLUP, associé aux matrices $\begin{pmatrix}21\\11\end{pmatrix}$ et $\begin{pmatrix}20\\15\end{pmatrix}$.
On prend dans un premier temps $r_1=21$ et $r_2=11$
Donc $x_1\equiv 9\times 21+16\times 11\equiv 365 \equiv 1\quad [26]$
et $x_2 \equiv 17 \times 21+25\times 11 \equiv 632 \equiv 8\quad [26]$
$\quad$
On prend ensuite $r_1=20$ et $r_2=15$
Donc $x_1\equiv 9\times 20+16\times 15\equiv 420\equiv 4\quad [26]$
et $x_2 \equiv 17 \times 20+25\times 15 \equiv 715 \equiv 13\quad [26]$
$\quad$
Ainsi VLUP est la version codé de BIEN.