Baccalauréat S Polynésie 9 septembre 2015 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (3 points)

Commun à tous les candidats

Géométrie dans l'espace

ABCDEFGH est un cube. I est le milieu de [AB], J est le milieu de [HDJ et K est le milieu de [HG]. On se place dans le repère $\left(\text{A}~;~ \vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$.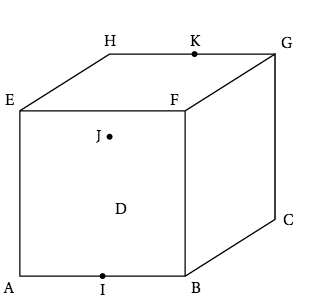

1. Démontrer que le vecteur $\vec{\text{CE}}$ est un vecteur normal au plan (IJK).
Dans le repère $\left(A;\vec{AB},\vec{AD},\vec{AE}\right)$, on a :
$C(1;1;0)$, $E(0;0;1)$, $I(0,5;0;0)$, $J(0;1;0,5)$ et $K(0,5;1;1)$
Ainsi $\vec{CE}(-1;-1;1)$, $\vec{IJ}(-0,5;1;0,5)$ et $\vec{IK}(0;1;1)$.
$\vec{IJ}$ et $\vec{IK}$ ne sont clairement pas colinéaires.
Par conséquent $\vec{CE}.\vec{IJ} = 0,5-1+0,5 = 0$ et $\vec{CE}.\vec{IK} = -1+1=0$.
Le vecteur $\vec{CE}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(IJK)$. Il est par conséquent normal à ce plan.
$\quad$
2. Démontrer que la droite (BD) est parallèle au plan (IJK).
On a $B(1;0;0)$ et $D(0;1;0)$. Ainsi $\vec{BD}(-1;1;0)$.
Onc $\vec{BD}.\vec{CE} = 1-1=0$.
Les deux vecteurs sont donc orthogonaux.
Puisque $\vec{CE}$ est normal à $(IJK)$ alors $\vec{BD}$ est parallèle à $(IJK)$.
$\quad$
3. Soit $M$ un point de la droite (CE). Quelle est la position du point $M$ sur la droite (CE) pour laquelle le plan (BD$M$) est parallèle au plan (IJK) ?
Soit $M(x;y;z)$ un point de $(CE)$. $\vec{BM}(x-1;y;z)$.
Une représentation paramétrique de la droite $(CE)$ est donnée par :
$$\begin{cases} x=1-t \\\\y=1-t\\\\z=t\end{cases} \qquad t\in\mathbb R$$
Les plans $(BDM)$ et $(IJK)$ soient parallèles si, et seulement si, $\vec{CE}$ est normal à $(BDM)$.
On sait déjà que $\vec{CE}$ est orthogonal à $\vec{BD}$.
Par conséquent, les deux plans sont parallèles si, et seulement si, $\vec{CE}$ et $\vec{BM}$ sont orthogonaux.
Cela est alors équivalent à $\vec{CE}.\vec{BM}=0 \Leftrightarrow 1-x-y+z=0$.
En injectant dans cette équation les coordonnées des points fournies par la représentation paramétrique de $(CE)$, on obtient :
$$1-(-1+t)-1+t+t=0 \Leftrightarrow 3t=1 \Leftrightarrow t=\dfrac{1}{3}$$ .
Ainsi, en reprenant la représentation paramétrique de $(CE)$, les coordonnées de $M$ sont $\left(\dfrac{2}{3};\dfrac{2}{3};\dfrac{1}{3}\right)$.
$\quad$