Baccalauréat S Polynésie 9 septembre 2015
Exercice 1 : 7 points
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
On rappelle que la partie réelle d'un nombre complexe $z$ est notée $Re (z)$.
- Déterminer l'écriture exponentielle du nombre complexe $u = 1 - \text{i}$.
- Déterminer, pour tout réel $\theta$, la forme algébrique et l'écriture exponentielle du nombre complexe $\text{e}^{\text{i} \theta} (1 - \text{i})$.
- Déduire des questions précédentes que, pour tout réel $\theta$,$\cos(\theta) + \sin(\theta) = \sqrt{2} \cos \left(\theta - \dfrac{\pi}{4}\right)$.
Partie B
Dans cette partie, on admet que, pour tout réel $\theta,\cos(\theta) + \sin(\theta) = \sqrt{2} \cos \left(\theta - \dfrac{\pi}{4}\right)$.
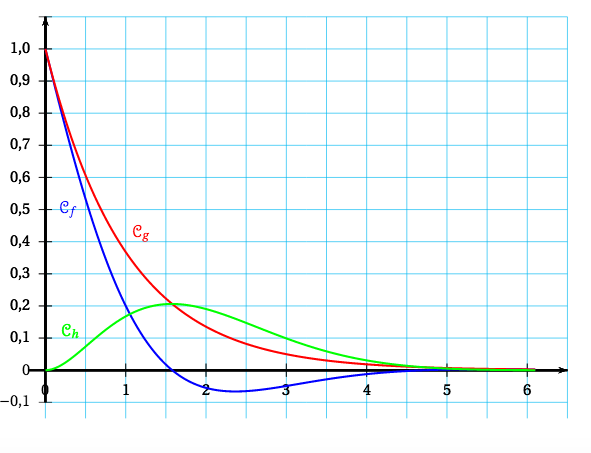
On considère les fonctions $f$ et $g$ définies sur l'intervalle $[0~;~+ \infty[$ par: \[f(x) = \text{e}^{-x} \cos(x)\quad \text{et}\quad g(x) = \text{e}^{-x}.\] On définit la fonction $h$ sur $[0~;~+ \infty[$ par $h(x) = g(x) - f(x)$. Les représentations graphiques $\mathcal{C}_f,\mathcal{C}_g$ et $\mathcal{C}_h$ des fonctions $f,g$ et $h$ sont données, en annexe, dans un repère orthogonal.
- Conjecturer:
- les limites des fonctions $f$ et $g$ en $+\infty$ ;
- la position relative de $\mathcal{C}_f$ par rapport à $\mathcal{C}_g$ ;
- la valeur de l'abscisse $x$ pour laquelle l'écart entre les deux courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ est maximal.
- Justifier que $\mathcal{C}_g$ est située au-dessus de $\mathcal{C}_f$ sur l'intervalle $[0~;~+ \infty[$.
- Démontrer que la droite d'équation $y = 0$ est asymptote horizontale aux courbes $\mathcal{C}_f$ et $\mathcal{C}_g$.
-
- On note $h'$ la fonction dérivée de la fonction $h$ sur l'intervalle $[0~;~+ \infty[$. Démontrer que, pour tout $x$ de l'intervalle $[0~;~+ \infty[$,$h'(x) = \text{e}^{-x} \left[\sqrt{2}\cos \left(x - \dfrac{\pi}{4}\right) - 1\right]$.
- Justifier que, sur l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$,$\sqrt{2} \cos \left(x - \dfrac{\pi}{4}\right) - 1 \geqslant 0$ et que, sur l'intervalle $\left[\dfrac{\pi}{2}~;~2\pi\right], \sqrt{2} \cos \left(x - \dfrac{\pi}{4}\right) - 1 \leqslant 0$.
- En déduire le tableau de variation de la fonction $h$ sur l'intervalle $[0~;~2\pi]$.
- On admet que, sur l'intervalle $[0~;~+ \infty[$, la fonction $H$ définie par \[H(x) = \dfrac{1}{2} \text{e}^{-x} [- 2 + \cos (x) - \sin (x)]\] est une primitive de la fonction $h$. On note $\mathcal{D}$ le domaine du plan délimité par les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$, et les droites d'équations $x = 0$ et $x = 2\pi$. Calculer l'aire $\mathcal{A}$ du domaine $\mathcal{D}$, exprimée en unités d'aire.
Correction de l'exercice 1 (5 points)
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
On rappelle que la partie réelle d'un nombre complexe $z$ est notée $Re (z)$.
- Déterminer l'écriture exponentielle du nombre complexe $u = 1 - \text{i}$. $|1-\text{i}|=\sqrt{2}$ donc
- Déterminer, pour tout réel $\theta$, la forme algébrique et l'écriture exponentielle du nombre complexe $\text{e}^{\text{i} \theta} (1 - \text{i})$. On a , pour tout $\theta \in \mathbb R$ :
- Déduire des questions précédentes que, pour tout réel $\theta$,$\cos(\theta) + \sin(\theta) = \sqrt{2} \cos \left(\theta - \dfrac{\pi}{4}\right)$. Par identification des parties réelles on obtient : $\cos \theta + \sin \theta = \sqrt{2}\cos\left(\theta-\dfrac{\pi}{4}\right)$.
$\begin{align*}1-\text{i} &= \sqrt{2}\left(\dfrac{1}{\sqrt{2}}-\dfrac{\text{i}}{\sqrt{2}}\right) \\\\
&=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\text{i}\right)\\\\
&=\sqrt{2}\text{ e}^{-\text{i}\pi/4}
\end{align*}$
$\quad$
$\begin{align*}\text{ e}^{\text{i} \theta}(1-\text{i}) &= \left(\cos(\theta) + \text{i} \sin(\theta)\right)(1-\text{i}) \\\\
&= \cos(\theta)-\text{i}\cos(\theta) +\text{i}\sin(\theta) +\sin (\theta) \\\\
&= \cos(\theta) + \sin(\theta) + \text{i}\left(\sin (\theta) – \cos (\theta)\right)
\end{align*}$
$\quad$
On a également la forme exponentielle :
$\text{ e}^{\text{i} \theta}(1-\text{i}) = \sqrt{2}\text{ e}^{\text{i}\theta}\text{ e}^{-\text{i}\pi/4} = \sqrt{2}\text{ e}^{\left(\theta – \pi/4\right)\text{i}}$
$\quad$
$\quad$
Partie B
Dans cette partie, on admet que, pour tout réel $\theta,\cos(\theta) + \sin(\theta) = \sqrt{2} \cos \left(\theta - \dfrac{\pi}{4}\right)$.
On considère les fonctions $f$ et $g$ définies sur l'intervalle $[0~;~+ \infty[$ par: \[f(x) = \text{e}^{-x} \cos(x)\quad \text{et}\quad g(x) = \text{e}^{-x}.\] On définit la fonction $h$ sur $[0~;~+ \infty[$ par $h(x) = g(x) - f(x)$. Les représentations graphiques $\mathcal{C}_f,\mathcal{C}_g$ et $\mathcal{C}_h$ des fonctions $f,g$ et $h$ sont données, en annexe, dans un repère orthogonal.
- Conjecturer:
- les limites des fonctions $f$ et $g$ en $+\infty$ ; Il semblerait que $\lim\limits_{x \to +\infty} f(x) = 0$ et $\lim\limits_{x \to +\infty} g(x) = 0$.
- la position relative de $\mathcal{C}_f$ par rapport à $\mathcal{C}_g$ ; Il semblerait que la courbe $\mathscr{C}_f$ soit toujours en-dessous de la courbe $\mathscr{C}_g$.
- la valeur de l'abscisse $x$ pour laquelle l'écart entre les deux courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ est maximal. L’écart semble entre ces deux courbes semble maximal pour $x=1,5$.
$\quad$
$\quad$
$\quad$ - Justifier que $\mathcal{C}_g$ est située au-dessus de $\mathcal{C}_f$ sur l'intervalle $[0~;~+ \infty[$. $\quad$
- Démontrer que la droite d'équation $y = 0$ est asymptote horizontale aux courbes $\mathcal{C}_f$ et $\mathcal{C}_g$. $\quad$
-
- On note $h'$ la fonction dérivée de la fonction $h$ sur l'intervalle $[0~;~+ \infty[$. Démontrer que, pour tout $x$ de l'intervalle $[0~;~+ \infty[$,$h'(x) = \text{e}^{-x} \left[\sqrt{2}\cos \left(x - \dfrac{\pi}{4}\right) - 1\right]$. La fonction $h$ est dérivable sur $[0;+\infty[$ en tant que produit et somme de fonctions dérivables sur cet intervalle.
- Justifier que, sur l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$,$\sqrt{2} \cos \left(x - \dfrac{\pi}{4}\right) - 1 \geqslant 0$ et que, sur l'intervalle $\left[\dfrac{\pi}{2}~;~2\pi\right], \sqrt{2} \cos \left(x - \dfrac{\pi}{4}\right) - 1 \leqslant 0$. Sur $\left[0;\dfrac{\pi}{2}\right]$, on a $-\dfrac{\pi}{4} \le x-\dfrac{\pi}{4} \le \dfrac{\pi}{4}$.
- En déduire le tableau de variation de la fonction $h$ sur l'intervalle $[0~;~2\pi]$. Sur $\left[0;\dfrac{\pi}{2}\right]$, on a $-\dfrac{\pi}{4} \le x-\dfrac{\pi}{4} \le \dfrac{\pi}{4}$.
$\begin{align*} h'(x) &=-\text{ e}^{-x} -\left(-\text{ e}^{-x}\cos(x)-\text{ e}^{-x}\sin(x)\right) \\\\
&=\text{ e}^{-x}\left(\cos(x)+\sin(x)-1\right) \\\\
&=\text{ e}^{-x}\left[\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right)-1\right] \qquad \text{d’après A.3}
\end{align*}$
$\quad$
Or sur $\left[-\dfrac{\pi}{4};\dfrac{\pi}{4}\right]$ on a $\dfrac{\sqrt{2}}{2}\le \cos(y) \le 1$.
Donc sur $\left[0;\dfrac{\pi}{2}\right]$, $1 \le \sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right)$.
Ainsi $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) – 1 \ge 0$ sur cet intervalle.
$\quad$
Sur $\left[\dfrac{\pi}{2};2\pi\right]$, on a $\dfrac{\pi}{4} \le x-\dfrac{\pi}{4} \le \dfrac{7\pi}{4}$.
Or sur $\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]$ on a $-1\le \cos(y) \le \dfrac{\sqrt{2}}{2}$.
Donc sur $\left[\dfrac{\pi}{2};2\pi\right]$, $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) \le 1$.
Ainsi $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) – 1 \le 0$ sur cet intervalle.
$\quad$
Or sur $\left[-\dfrac{\pi}{4};\dfrac{\pi}{4}\right]$ on a $\dfrac{\sqrt{2}}{2}\le \cos(y) \le 1$.
Donc sur $\left[0;\dfrac{\pi}{2}\right]$, $1 \le \sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right)$.
Ainsi $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) – 1 \ge 0$ sur cet intervalle.
$\quad$
Sur $\left[\dfrac{\pi}{2};2\pi\right]$, on a $\dfrac{\pi}{4} \le x-\dfrac{\pi}{4} \le \dfrac{7\pi}{4}$.
Or sur $\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]$ on a $-1\le \cos(y) \le \dfrac{\sqrt{2}}{2}$.
Donc sur $\left[\dfrac{\pi}{2};2\pi\right]$, $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) \le 1$.
Ainsi $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) – 1 \le 0$ sur cet intervalle.
$\quad$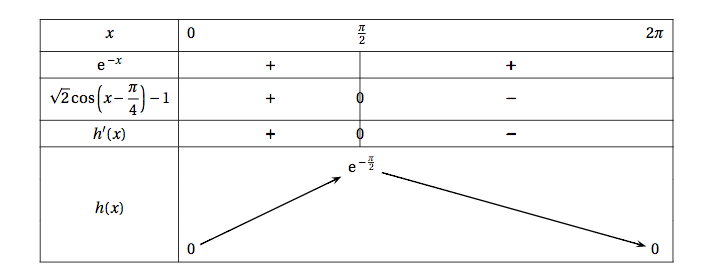
- On admet que, sur l'intervalle $[0~;~+ \infty[$, la fonction $H$ définie par \[H(x) = \dfrac{1}{2} \text{e}^{-x} [- 2 + \cos (x) - \sin (x)]\] est une primitive de la fonction $h$. On note $\mathcal{D}$ le domaine du plan délimité par les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$, et les droites d'équations $x = 0$ et $x = 2\pi$. Calculer l'aire $\mathcal{A}$ du domaine $\mathcal{D}$, exprimée en unités d'aire. La fonction $h$ est continue (car dérivable) et positive sur $[0;2\pi]$.
$\begin{align*} g(x)-f(x)&=e^{-x}-e^{-x}\cos(x)\\\\
&=e^{-x}\left(1-\cos(x)\right)
\end{align*}$
Or la fonction exponentielle est strictement positive et pour tout réel $x$ on a, $ \cos(x) \le 1$.
Par conséquent $g(x)-f(x) \ge 0$ et la courbe $\mathscr{C}_g$ est au-dessus de $\mathscr{C}_f$ sur $[0;+\infty[$.
$\quad$
$\left. \begin{array}{l} \lim\limits_{x \to +\infty} -x = -\infty\\\\ \lim\limits_{x \to -\infty} \text{ e}^x=0 \end{array}\right\} \lim\limits_{x \to +\infty} \text{ e}^{-x} = 0$
La droite d’équation $y=0$ est donc asymptote à la courbe $\mathscr{C}_g$.
$\quad$
Puisque, pour tout réel $x$ de $[0;+\infty[$, on a $-1 \le \cos(x) \le 1$, alors $-\text{ e}^{-x} \le f(x) \text{ e}^{-x}$.
Or $\lim\limits_{x \to +\infty} \text{ e}^{-x} = 0$.
D’après le théorème des gendarmes, on a donc $\lim\limits_{x \to +\infty} f(x) = 0$.
La droite d’équation $y=0$ est, par conséquent, également asymptote à la courbe $\mathscr{C}_f$.
$\quad$
Ainsi l’aire du domaine $\mathscr{D}$ est donnée par :
$\begin{align*} \mathscr{A} &=\displaystyle \int_0^{2\pi} h(x)\mathrm{d}x \\\\
&= H(2\pi)-H(0) \\\\
&= \dfrac{1}{2}\text{ e}^{-2\pi}(-2+1) – \dfrac{1}{2}(-2+1)\\\\
&=\dfrac{1}{2}\left(1-\text{ e}^{-2\pi}\right) \text{u.a}
\end{align*}$
$\quad$

Exercice 2 : 5 points
Partie A
On étudie une maladie dans la population d'un pays. On a constaté que le taux, en nanogrammes par millilitre $\left(\text{ng.mL}^{-1}\right)$, d'une substance Gamma présente dans le sang est plus élevé chez les personnes atteintes de cette maladie que chez les personnes qui n'en sont pas atteintes.
- Le taux de cette substance Gamma dans la population des personnes qui ne sont pas atteintes par la maladie est modélisé par une variable aléatoire $T$ qui suit la loi normale d'espérance $\mu = 40$ et d'écart-type $\sigma = 8$. On choisit au hasard une personne parmi celles qui ne sont pas atteintes par la maladie étudiée. Calculer la probabilité que le taux dans le sang de la substance Gamma soit supérieur à 60 ng.mL$^{-1}$.
- Des études ont mis en évidence que le taux moyen de la substance Gamma chez les personnes atteintes par la maladie étudiée est de 50 ng.mL$^{-1}$ et que 10% d'entre elles ont un taux de substance Gamma inférieur à 43 ng.mL$^{-1}$. On appelle $T'$ la variable aléatoire qui modélise le taux de la substance Gamma en ng.mL$^{-1}$ chez une personne atteinte par la maladie étudiée. On admet que $T'$ suit la loi normale d'espérance $\mu'$ et d'écart-type $\sigma'$. Préciser la valeur de $\mu'$ et déterminer la valeur de $\sigma'$.
Partie B
Pour dépister chez une personne la maladie étudiée, on effectue une prise de sang. On considère que le dépistage est positif si le taux de la substance Gamma est supérieur ou égal à 45 ng.mL$^{-1}$. Une personne étant choisie au hasard dans la population, on appelle :
- $M$ l'évènement « le patient est atteint par la maladie étudiée » ;
- $D$ l'évènement « le patient a un dépistage positif».
On admet que :
- 82% des personnes atteintes par la maladie étudiée ont un dépistage positif ;
- 73% des personnes non atteintes par cette maladie ont un dépistage négatif.
On sait de plus que 10% de la population étudiée est atteinte par cette maladie.
- Démontrer que la probabilité qu'un patient ait un dépistage positif est de $0,325$.
- Calculer $P_{\overline{D}}(M)$. Interpréter ce résultat.
- Un patient a un dépistage positif. Le médecin le rassure en lui indiquant qu'il n'a qu'une chance sur quatre d'avoir contracté la maladie. Qu'en pensez- vous ?
Partie C
Lors du dépistage précédent, la prise de sang est effectuée chez des sujets à jeun. Les données montrent que 82% des patients malades ont un dépistage positif. Pour améliorer le confort des personnes susceptibles de subir cet examen sanguin, on souhaite vérifier si le fait d'être à jeun est une condition indispensable dans le protocole. On considère un groupe de $300$ personnes malades sur lesquelles la prise de sang n'est pas effectuée à jeun. Le dépistage se révèle positif pour 74% d'entre elles. Ce dépistage peut-il être effectué sur des personnes qui ne sont pas à jeun ?
Correction de l'exercice 2 (5 points)
Partie A
On étudie une maladie dans la population d'un pays. On a constaté que le taux, en nanogrammes par millilitre $\left(\text{ng.mL}^{-1}\right)$, d'une substance Gamma présente dans le sang est plus élevé chez les personnes atteintes de cette maladie que chez les personnes qui n'en sont pas atteintes.
- Le taux de cette substance Gamma dans la population des personnes qui ne sont pas atteintes par la maladie est modélisé par une variable aléatoire $T$ qui suit la loi normale d'espérance $\mu = 40$ et d'écart-type $\sigma = 8$. On choisit au hasard une personne parmi celles qui ne sont pas atteintes par la maladie étudiée. Calculer la probabilité que le taux dans le sang de la substance Gamma soit supérieur à 60 ng.mL$^{-1}$. On veut calculer $P(T \ge 60) = 0,5 – P(40 \le T \le 60) \approx 0,0062$
- Des études ont mis en évidence que le taux moyen de la substance Gamma chez les personnes atteintes par la maladie étudiée est de 50 ng.mL$^{-1}$ et que 10% d'entre elles ont un taux de substance Gamma inférieur à 43 ng.mL$^{-1}$. On appelle $T'$ la variable aléatoire qui modélise le taux de la substance Gamma en ng.mL$^{-1}$ chez une personne atteinte par la maladie étudiée. On admet que $T'$ suit la loi normale d'espérance $\mu'$ et d'écart-type $\sigma'$. Préciser la valeur de $\mu'$ et déterminer la valeur de $\sigma'$. D’après l’énoncé, on a $\mu’=50$.
2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$
On sait également que :
$\begin{align*} P(T’ \le 43) = 0,1 & \Leftrightarrow P\left(\dfrac{T’-50}{\sigma’} \le \dfrac{43-50}{\sigma’}\right)=0,1 \\\\
&\Leftrightarrow P\left(\dfrac{T’-50}{\sigma’} \le -\dfrac{7}{\sigma’}\right) = 0,1
\end{align*}$
Or la variable aléatoire $\dfrac{T’-50}{\sigma’}$ suit la loi normale centrée réduite.
Par conséquent à l’aide de la touche Inverve Loi Normale on obtient $-\dfrac{7}{\sigma’} \approx -1,2816$ soit $\sigma’ \approx 5,4621$.
$\quad$
Partie B
Pour dépister chez une personne la maladie étudiée, on effectue une prise de sang. On considère que le dépistage est positif si le taux de la substance Gamma est supérieur ou égal à 45 ng.mL$^{-1}$. Une personne étant choisie au hasard dans la population, on appelle :
- $M$ l'évènement « le patient est atteint par la maladie étudiée » ;
- $D$ l'évènement « le patient a un dépistage positif».
On admet que :
- 82% des personnes atteintes par la maladie étudiée ont un dépistage positif ;
- 73% des personnes non atteintes par cette maladie ont un dépistage négatif.
On sait de plus que 10% de la population étudiée est atteinte par cette maladie.
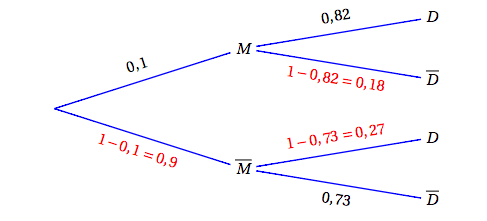
- Démontrer que la probabilité qu'un patient ait un dépistage positif est de $0,325$. On peut résumer la situation par un arbre pondéré :
- Calculer $P_{\overline{D}}(M)$. Interpréter ce résultat. $\begin{align*} p_{\overline{D}}(M) &= \dfrac{p\left(M \cap \overline{D}\right)}{p\left(\overline{D}\right)} \\\\
- Un patient a un dépistage positif. Le médecin le rassure en lui indiquant qu'il n'a qu'une chance sur quatre d'avoir contracté la maladie. Qu'en pensez- vous ? Calculons :
 D’après la formule des probabilités totales, on a alors :
D’après la formule des probabilités totales, on a alors :$\begin{align*} p(D)&=p(M\cap D) + p\left(D \cap \overline{M}\right) \\\\
&=0,1 \times 0,82 + 0,9 \times 0,27 \\\\
&=0,325
\end{align*}$
$\quad$
&= \dfrac{0,1 \times 0,18}{1-0,325}\\\\
&=\dfrac{2}{75}\\\\
&\approx 0,0267
\end{align*}$
Cela signifie donc qu’environ $2,67\%$ des individus ayant un dépistage négatif sont atteints par la maladie étudiée.
$\quad$
$\begin{align*} p_D(M) &= \dfrac{p(D\cap M)}{p(D)} \\\\
&= \dfrac{0,1 \times 0,82}{0,325} \\\\
& = \dfrac{82}{325} \\\\
& \approx 0,2523
\end{align*}$
Il y a donc effectivement environ une chance sur quatre que le patient ait contracté la maladie.
$\quad$
Partie C
On a $n=300$ et $p=0,82$
Ainsi $n\ge 30$, $np=246\ge 5$ et $n(1-p)=54\ge 5$.
Les conditions sont donc vérifiées pour déterminer un intervalle de fluctuation asymptotique. Le seuil choisi sera de $95\%$
$$\begin{align*} I_{300} &= \left[0,82-1,96\sqrt{\dfrac{0,82 \times 0,18}{300}};0,82+1,96\sqrt{\dfrac{0,82 \times 0,18}{300}}\right] \\\\
& \approx[0,77;0,87]
\end{align*}$$
Or la fréquence observée quand les personnes ne sont pas à jeun est $f=0,74 \notin I_{300}$
Ainsi ce dépistage ne peut pas, au risque de $5\%$, être effectué sur des personnes qui ne sont pas à jeun.
Exercice 3 : 3 points
ABCDEFGH est un cube. I est le milieu de [AB], J est le milieu de [HDJ et K est le milieu de [HG]. On se place dans le repère $\left(\text{A}~;~ \vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$.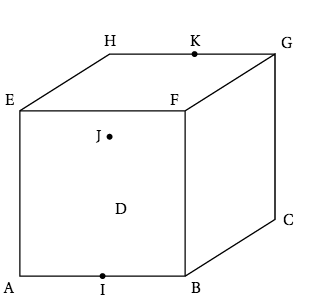
- Démontrer que le vecteur $\vec{\text{CE}}$ est un vecteur normal au plan (IJK).
- Démontrer que la droite (BD) est parallèle au plan (IJK).
- Soit $M$ un point de la droite (CE). Quelle est la position du point $M$ sur la droite (CE) pour laquelle le plan (BD$M$) est parallèle au plan (IJK) ?
Correction de l'exercice 3 (3 points)
ABCDEFGH est un cube. I est le milieu de [AB], J est le milieu de [HDJ et K est le milieu de [HG]. On se place dans le repère $\left(\text{A}~;~ \vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$.
- Démontrer que le vecteur $\vec{\text{CE}}$ est un vecteur normal au plan (IJK). Dans le repère $\left(A;\vec{AB},\vec{AD},\vec{AE}\right)$, on a :
- Démontrer que la droite (BD) est parallèle au plan (IJK). On a $B(1;0;0)$ et $D(0;1;0)$. Ainsi $\vec{BD}(-1;1;0)$.
- Soit $M$ un point de la droite (CE). Quelle est la position du point $M$ sur la droite (CE) pour laquelle le plan (BD$M$) est parallèle au plan (IJK) ? Soit $M(x;y;z)$ un point de $(CE)$. $\vec{BM}(x-1;y;z)$.
$C(1;1;0)$, $E(0;0;1)$, $I(0,5;0;0)$, $J(0;1;0,5)$ et $K(0,5;1;1)$
Ainsi $\vec{CE}(-1;-1;1)$, $\vec{IJ}(-0,5;1;0,5)$ et $\vec{IK}(0;1;1)$.
$\vec{IJ}$ et $\vec{IK}$ ne sont clairement pas colinéaires.
Par conséquent $\vec{CE}.\vec{IJ} = 0,5-1+0,5 = 0$ et $\vec{CE}.\vec{IK} = -1+1=0$.
Le vecteur $\vec{CE}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(IJK)$. Il est par conséquent normal à ce plan.
$\quad$
Onc $\vec{BD}.\vec{CE} = 1-1=0$.
Les deux vecteurs sont donc orthogonaux.
Puisque $\vec{CE}$ est normal à $(IJK)$ alors $\vec{BD}$ est parallèle à $(IJK)$.
$\quad$
Une représentation paramétrique de la droite $(CE)$ est donnée par :
$$\begin{cases} x=1-t \\\\y=1-t\\\\z=t\end{cases} \qquad t\in\mathbb R$$
Les plans $(BDM)$ et $(IJK)$ soient parallèles si, et seulement si, $\vec{CE}$ est normal à $(BDM)$.
On sait déjà que $\vec{CE}$ est orthogonal à $\vec{BD}$.
Par conséquent, les deux plans sont parallèles si, et seulement si, $\vec{CE}$ et $\vec{BM}$ sont orthogonaux.
Cela est alors équivalent à $\vec{CE}.\vec{BM}=0 \Leftrightarrow 1-x-y+z=0$.
En injectant dans cette équation les coordonnées des points fournies par la représentation paramétrique de $(CE)$, on obtient :
$$1-(-1+t)-1+t+t=0 \Leftrightarrow 3t=1 \Leftrightarrow t=\dfrac{1}{3}$$.
Ainsi, en reprenant la représentation paramétrique de $(CE)$, les coordonnées de $M$ sont $\left(\dfrac{2}{3};\dfrac{2}{3};\dfrac{1}{3}\right)$.
$\quad$
Exercice 4 5 points
Correction de l'exercice 4 5 points
Spécialité 5 points
Pour tout entier naturel $n$ non nul, on appelle $S(n)$ le nombre égal à la somme des diviseurs positifs de $n$.
- Vérifier que $S(6) = 12$ et calculer $S(7)$.
-
- Démontrer que, pour tout entier naturel $n$ supérieur ou égal à 2, $S(n) \geqslant 1 + n$.
- Quels sont les entiers naturels $n$ tels que $S(n) = 1 + n$ ?
- On suppose dans cette question que $n$ s'écrit $p \times q$ où $p$ et $q$ sont des nombres premiers distincts.
- Démontrer que $S(n) = (1 + p)(1 + q)$.
- On considère la proposition suivante : « Pour tous entiers naturels $n$ et $m$ non nuls distincts, $S(n \times m) = S(n) \times S(m)$ ». Cette proposition est-elle vraie ou fausse ? Justifier.
- On suppose dans cette question que l'entier $n$ s'écrit $p^k$, où $p$ est un nombre premier et $k$ un nombre entier naturel non nul.
- Quels sont les diviseurs de $n$ ?
- En déduire que $S(n) = \dfrac{1- p^{k+1}}{1- p}$.
- On suppose dans cette question que $n$ s'écrit $p^{13} \times q^7$, où $p$ et $q$ sont des nombres premiers distincts.
- Soit $m$ un entier naturel. Démontrer que $m$ divise $n$ si, et seulement si, il existe deux nombres entiers $s$ et $t$ avec $0 \leqslant s \leqslant 13$ et $0 \leqslant t \leqslant 7$ tels que $m = p^s \times q^t$.
- Démontrer que $S(n) = \dfrac{1 - p^{14}}{1 - p} \times \dfrac{1 - q^8}{1 - q}$.
Correction de l'exercice de Spécialité 5 points
Pour tout entier naturel $n$ non nul, on appelle $S(n)$ le nombre égal à la somme des diviseurs positifs de $n$.
- Vérifier que $S(6) = 12$ et calculer $S(7)$. Les diviseurs positifs de $6$, sont $1,2,3$ et $6$. Ainsi $S(6) = 12$.
-
- Démontrer que, pour tout entier naturel $n$ supérieur ou égal à 2, $S(n) \geqslant 1 + n$. Pour tout entier naturel $n$ supérieur à $2$, $1$ et $n$ sont des diviseurs positifs de $n$ distincts.
- Quels sont les entiers naturels $n$ tels que $S(n) = 1 + n$ ? Pour que $S(n)=1+n$ il faut que $n$ ne soit divisible exactement par $2$ nombres : $1$ et lui-même. C’est donc un nombre premier.
Ainsi $S(n) \ge 1+n$.
$\quad$
$\quad$ - On suppose dans cette question que $n$ s'écrit $p \times q$ où $p$ et $q$ sont des nombres premiers distincts.
- Démontrer que $S(n) = (1 + p)(1 + q)$. Si $n=p\times q$ avec $p$ et $q$ deux nombres premiers distincts, alors les seuls diviseurs positifs de $n$ sont $1$, $p$, $q$ et $pq$.
- On considère la proposition suivante : « Pour tous entiers naturels $n$ et $m$ non nuls distincts, $S(n \times m) = S(n) \times S(m)$ ». Cette proposition est-elle vraie ou fausse ? Justifier. Prenons $n=4$ et $m=2$.
Par conséquent $S(n)=1+p+q+pq = (1+p)(1+q)$.
$\quad$
Les diviseurs positifs de $n$ sont $1$, $2$ et $4$. Ainsi $S(4)=7$.
Puisque $2$ est premier, $S(2) = 3$
Les diviseurs positifs de $8$ sont $1$, $2$, $4$ et $8$. Ainsi $S(8) = 15$.
Par conséquent $S(8) \neq S(4) \times S(2)$.
La proposition faite est donc fausse.
$\quad$ - On suppose dans cette question que l'entier $n$ s'écrit $p^k$, où $p$ est un nombre premier et $k$ un nombre entier naturel non nul.
- Quels sont les diviseurs de $n$ ? $n=p^k$ ou $p$ est un nombre premier et $k$ un nombre entier naturel non nul.
- En déduire que $S(n) = \dfrac{1- p^{k+1}}{1- p}$. Ainsi $S(n) = \displaystyle \sum_{i=0}^k p^i= 1+p+p^2+\ldots +p^k = \dfrac{1-p^{k+1}}{1-p}$.
Les diviseurs de $n$ sont donc les $p^i$ pour $i\in \left\{0;1;\ldots;k\right\}$.
$\quad$
$\quad$ - On suppose dans cette question que $n$ s'écrit $p^{13} \times q^7$, où $p$ et $q$ sont des nombres premiers distincts.
- Soit $m$ un entier naturel. Démontrer que $m$ divise $n$ si, et seulement si, il existe deux nombres entiers $s$ et $t$ avec $0 \leqslant s \leqslant 13$ et $0 \leqslant t \leqslant 7$ tels que $m = p^s \times q^t$. $n=p^{13}\times q^7$ avec $p$ et $q$ deux nombres premiers distincts.
- Démontrer que $S(n) = \dfrac{1 - p^{14}}{1 - p} \times \dfrac{1 - q^8}{1 - q}$. On a donc :
Soit $m$ un diviseur de $n$.
Supposons que $m$ soit divisible par un nombre premier $d$ différent de $p$ et $q$.
Puisque $d$ divise $m$, il divise également $n$.
Cela signifie donc que $m$ divise soit $p$ soit $q$. Ce qui est impossible.
Donc $m$ s’écrit sous la forme $p^s\times q^t$ où $s$ et $t$ sont des entiers naturels.
$s \le 13$ car $p^{14}$ ne divise pas $n$. De même $t \le 7$ car $q^8$ ne divise pas $n$.
Par conséquent, il existe deux entiers naturels $s$ et $t$, tels que $0 \le s\le 13$ et $0 \le t \le 7$ tel que $m=p^s\times q^t$
$\quad$
Réciproquement supposons qu’il existe deux entiers naturels $s$ et $t$, tels que $0 \le s\le 13$ et $0 \le t \le 7$ tel que $m=p^s\times q^t$
Alors $n=p^{13}\times q^7 = p^s\times p^{13-s}\times q^t\times q^{7-t} = m \times p^{13-s}\times q^{7-t}$.
$m$ divise bien $n$.
$\quad$
$$\begin{align*} S(n) &= \displaystyle \sum_{s=0}^{13} \sum_{t=0}^{7} p^s\times q^t \\\\
&= \sum_{s=0}^{13} p^s\times\sum_{t=0}^{7} q^t \\\\
&= \sum_{s=0}^{13} p^s\times\dfrac{1-q^8}{1-q} \\\\
&= \left(\sum_{s=0}^{13} p^s\right) \times\dfrac{1-q^8}{1-q}\\\\
&= \dfrac{1-p^{14}}{1-p} \times \dfrac{1-q^8}{1-q}
\end{align*}$$
Les diviseurs positifs de $7$ sont $1$ et $7$. Ainsi $S(7)=8$.
$\quad$
- Vues: 38853
