Baccalauréat S Polynésie 9 septembre 2015 - Correction Exercice 1
Page 2 sur 10
Correction de l'exercice 1 (5 points)
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
On rappelle que la partie réelle d'un nombre complexe $z$ est notée $Re (z)$.
- Déterminer l'écriture exponentielle du nombre complexe $u = 1 - \text{i}$. $|1-\text{i}|=\sqrt{2}$ donc
- Déterminer, pour tout réel $\theta$, la forme algébrique et l'écriture exponentielle du nombre complexe $\text{e}^{\text{i} \theta} (1 - \text{i})$. On a , pour tout $\theta \in \mathbb R$ :
- Déduire des questions précédentes que, pour tout réel $\theta$,$\cos(\theta) + \sin(\theta) = \sqrt{2} \cos \left(\theta - \dfrac{\pi}{4}\right)$. Par identification des parties réelles on obtient : $\cos \theta + \sin \theta = \sqrt{2}\cos\left(\theta-\dfrac{\pi}{4}\right)$.
$\begin{align*}1-\text{i} &= \sqrt{2}\left(\dfrac{1}{\sqrt{2}}-\dfrac{\text{i}}{\sqrt{2}}\right) \\\\
&=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\text{i}\right)\\\\
&=\sqrt{2}\text{ e}^{-\text{i}\pi/4}
\end{align*}$
$\quad$
$\begin{align*}\text{ e}^{\text{i} \theta}(1-\text{i}) &= \left(\cos(\theta) + \text{i} \sin(\theta)\right)(1-\text{i}) \\\\
&= \cos(\theta)-\text{i}\cos(\theta) +\text{i}\sin(\theta) +\sin (\theta) \\\\
&= \cos(\theta) + \sin(\theta) + \text{i}\left(\sin (\theta) – \cos (\theta)\right)
\end{align*}$
$\quad$
On a également la forme exponentielle :
$\text{ e}^{\text{i} \theta}(1-\text{i}) = \sqrt{2}\text{ e}^{\text{i}\theta}\text{ e}^{-\text{i}\pi/4} = \sqrt{2}\text{ e}^{\left(\theta – \pi/4\right)\text{i}}$
$\quad$
$\quad$
Partie B
Dans cette partie, on admet que, pour tout réel $\theta,\cos(\theta) + \sin(\theta) = \sqrt{2} \cos \left(\theta - \dfrac{\pi}{4}\right)$.
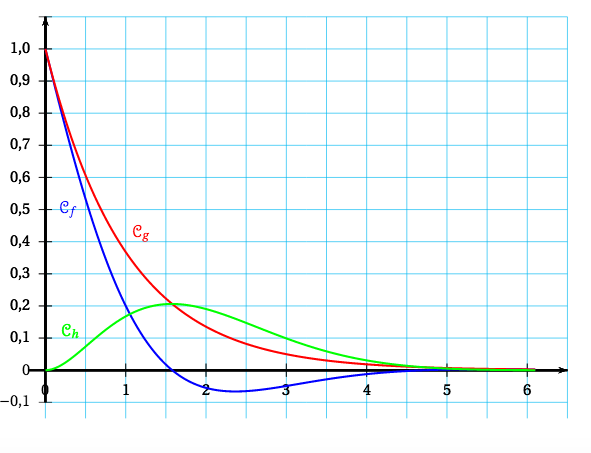
On considère les fonctions $f$ et $g$ définies sur l'intervalle $[0~;~+ \infty[$ par: \[f(x) = \text{e}^{-x} \cos(x)\quad \text{et}\quad g(x) = \text{e}^{-x}.\] On définit la fonction $h$ sur $[0~;~+ \infty[$ par $h(x) = g(x) - f(x)$. Les représentations graphiques $\mathcal{C}_f,\mathcal{C}_g$ et $\mathcal{C}_h$ des fonctions $f,g$ et $h$ sont données, en annexe, dans un repère orthogonal.
- Conjecturer:
- les limites des fonctions $f$ et $g$ en $+\infty$ ; Il semblerait que $\lim\limits_{x \to +\infty} f(x) = 0$ et $\lim\limits_{x \to +\infty} g(x) = 0$.
- la position relative de $\mathcal{C}_f$ par rapport à $\mathcal{C}_g$ ; Il semblerait que la courbe $\mathscr{C}_f$ soit toujours en-dessous de la courbe $\mathscr{C}_g$.
- la valeur de l'abscisse $x$ pour laquelle l'écart entre les deux courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ est maximal. L’écart semble entre ces deux courbes semble maximal pour $x=1,5$.
$\quad$
$\quad$
$\quad$ - Justifier que $\mathcal{C}_g$ est située au-dessus de $\mathcal{C}_f$ sur l'intervalle $[0~;~+ \infty[$. $\quad$
- Démontrer que la droite d'équation $y = 0$ est asymptote horizontale aux courbes $\mathcal{C}_f$ et $\mathcal{C}_g$. $\quad$
-
- On note $h'$ la fonction dérivée de la fonction $h$ sur l'intervalle $[0~;~+ \infty[$. Démontrer que, pour tout $x$ de l'intervalle $[0~;~+ \infty[$,$h'(x) = \text{e}^{-x} \left[\sqrt{2}\cos \left(x - \dfrac{\pi}{4}\right) - 1\right]$. La fonction $h$ est dérivable sur $[0;+\infty[$ en tant que produit et somme de fonctions dérivables sur cet intervalle.
- Justifier que, sur l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$,$\sqrt{2} \cos \left(x - \dfrac{\pi}{4}\right) - 1 \geqslant 0$ et que, sur l'intervalle $\left[\dfrac{\pi}{2}~;~2\pi\right], \sqrt{2} \cos \left(x - \dfrac{\pi}{4}\right) - 1 \leqslant 0$. Sur $\left[0;\dfrac{\pi}{2}\right]$, on a $-\dfrac{\pi}{4} \le x-\dfrac{\pi}{4} \le \dfrac{\pi}{4}$.
- En déduire le tableau de variation de la fonction $h$ sur l'intervalle $[0~;~2\pi]$. Sur $\left[0;\dfrac{\pi}{2}\right]$, on a $-\dfrac{\pi}{4} \le x-\dfrac{\pi}{4} \le \dfrac{\pi}{4}$.
$\begin{align*} h'(x) &=-\text{ e}^{-x} -\left(-\text{ e}^{-x}\cos(x)-\text{ e}^{-x}\sin(x)\right) \\\\
&=\text{ e}^{-x}\left(\cos(x)+\sin(x)-1\right) \\\\
&=\text{ e}^{-x}\left[\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right)-1\right] \qquad \text{d’après A.3}
\end{align*}$
$\quad$
Or sur $\left[-\dfrac{\pi}{4};\dfrac{\pi}{4}\right]$ on a $\dfrac{\sqrt{2}}{2}\le \cos(y) \le 1$.
Donc sur $\left[0;\dfrac{\pi}{2}\right]$, $1 \le \sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right)$.
Ainsi $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) – 1 \ge 0$ sur cet intervalle.
$\quad$
Sur $\left[\dfrac{\pi}{2};2\pi\right]$, on a $\dfrac{\pi}{4} \le x-\dfrac{\pi}{4} \le \dfrac{7\pi}{4}$.
Or sur $\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]$ on a $-1\le \cos(y) \le \dfrac{\sqrt{2}}{2}$.
Donc sur $\left[\dfrac{\pi}{2};2\pi\right]$, $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) \le 1$.
Ainsi $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) – 1 \le 0$ sur cet intervalle.
$\quad$
Or sur $\left[-\dfrac{\pi}{4};\dfrac{\pi}{4}\right]$ on a $\dfrac{\sqrt{2}}{2}\le \cos(y) \le 1$.
Donc sur $\left[0;\dfrac{\pi}{2}\right]$, $1 \le \sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right)$.
Ainsi $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) – 1 \ge 0$ sur cet intervalle.
$\quad$
Sur $\left[\dfrac{\pi}{2};2\pi\right]$, on a $\dfrac{\pi}{4} \le x-\dfrac{\pi}{4} \le \dfrac{7\pi}{4}$.
Or sur $\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]$ on a $-1\le \cos(y) \le \dfrac{\sqrt{2}}{2}$.
Donc sur $\left[\dfrac{\pi}{2};2\pi\right]$, $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) \le 1$.
Ainsi $\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right) – 1 \le 0$ sur cet intervalle.
$\quad$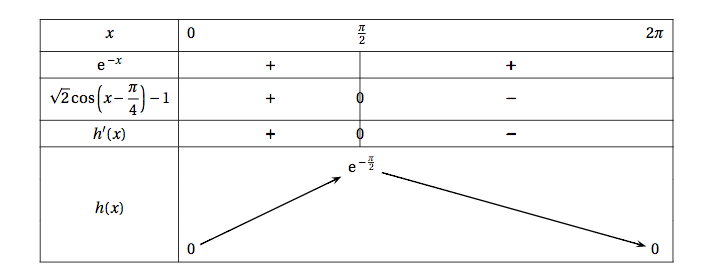
- On admet que, sur l'intervalle $[0~;~+ \infty[$, la fonction $H$ définie par \[H(x) = \dfrac{1}{2} \text{e}^{-x} [- 2 + \cos (x) - \sin (x)]\] est une primitive de la fonction $h$. On note $\mathcal{D}$ le domaine du plan délimité par les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$, et les droites d'équations $x = 0$ et $x = 2\pi$. Calculer l'aire $\mathcal{A}$ du domaine $\mathcal{D}$, exprimée en unités d'aire. La fonction $h$ est continue (car dérivable) et positive sur $[0;2\pi]$.
$\begin{align*} g(x)-f(x)&=e^{-x}-e^{-x}\cos(x)\\\\
&=e^{-x}\left(1-\cos(x)\right)
\end{align*}$
Or la fonction exponentielle est strictement positive et pour tout réel $x$ on a, $ \cos(x) \le 1$.
Par conséquent $g(x)-f(x) \ge 0$ et la courbe $\mathscr{C}_g$ est au-dessus de $\mathscr{C}_f$ sur $[0;+\infty[$.
$\quad$
$\left. \begin{array}{l} \lim\limits_{x \to +\infty} -x = -\infty\\\\ \lim\limits_{x \to -\infty} \text{ e}^x=0 \end{array}\right\} \lim\limits_{x \to +\infty} \text{ e}^{-x} = 0$
La droite d’équation $y=0$ est donc asymptote à la courbe $\mathscr{C}_g$.
$\quad$
Puisque, pour tout réel $x$ de $[0;+\infty[$, on a $-1 \le \cos(x) \le 1$, alors $-\text{ e}^{-x} \le f(x) \text{ e}^{-x}$.
Or $\lim\limits_{x \to +\infty} \text{ e}^{-x} = 0$.
D’après le théorème des gendarmes, on a donc $\lim\limits_{x \to +\infty} f(x) = 0$.
La droite d’équation $y=0$ est, par conséquent, également asymptote à la courbe $\mathscr{C}_f$.
$\quad$
Ainsi l’aire du domaine $\mathscr{D}$ est donnée par :
$\begin{align*} \mathscr{A} &=\displaystyle \int_0^{2\pi} h(x)\mathrm{d}x \\\\
&= H(2\pi)-H(0) \\\\
&= \dfrac{1}{2}\text{ e}^{-2\pi}(-2+1) – \dfrac{1}{2}(-2+1)\\\\
&=\dfrac{1}{2}\left(1-\text{ e}^{-2\pi}\right) \text{u.a}
\end{align*}$
$\quad$
- Vues: 39385
