Baccalauréat S Antilles-Guyane septembre 2015
Exercice 1 6 points
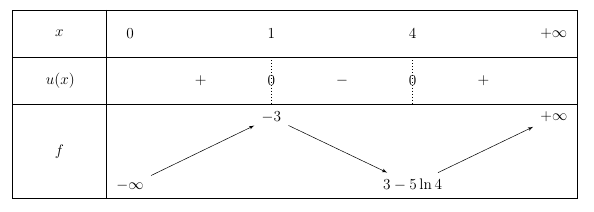
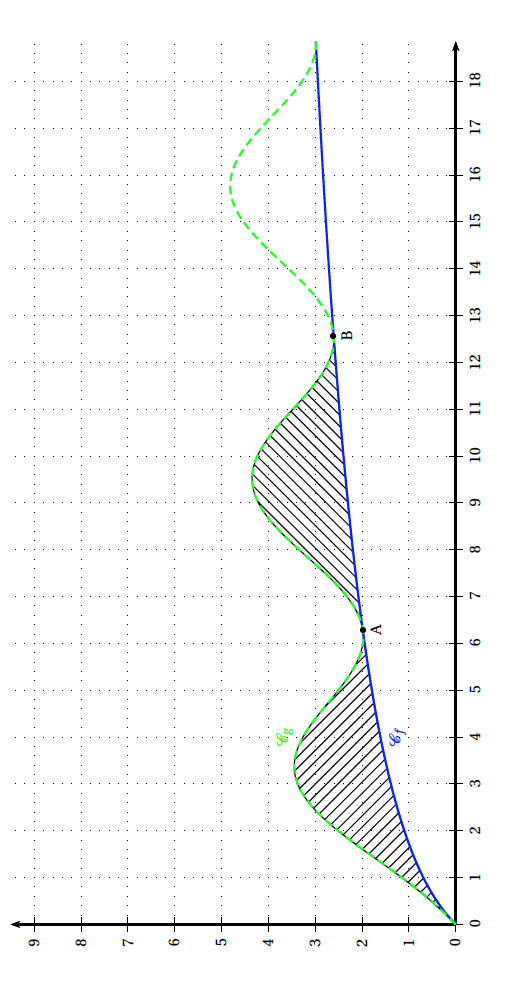
Soit $n$ un entier naturel non nul. On considère la fonction $f_n$ définie et dérivable sur l'ensemble $\mathbb R$ des nombres réels par \[f_n(x) = x^2 \text{e}^{- 2nx}.\] On note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ dans un repère orthogonal. On définit, pour tout entier naturel $n$ non nul, $I_n = \displaystyle\int_0^1 f_n(x)\: \text{d}x$.
Partie A : Étude de la fonction $f_1$
- La fonction $f_1$ est définie sur $\mathbb R$ par $f_1(x) = x^2\text{e}^{-2x}$. On admet que $f_1$ est dérivable sur $\mathbb R$ et on note $f_1'$ sa dérivée.
- Justifier que pour tout réel $x,\: f_1'(x) = 2x\text{e}^{-2x}(1 - x)$.
- Étudier les variations de la fonction $f_1$ sur $\mathbb R$.
- Déterminer la limite de $f_1$ en $- \infty$.
- Vérifier que pour tout réel $x,\: f_1(x) = \left(\dfrac{x}{\text{e}^x}\right)^2$. En déduire la limite de $f_1$ en $+ \infty$.
- En utilisant un système de calcul formel, on trouve qu'une primitive $F_1$ de la fonction $f_1$ est donnée par $F_1(x) = - \text{e}^{-2x}\left(\dfrac{x^2}{2} + \dfrac{x}{2} + \dfrac{1}{4}\right)$. En déduire la valeur exacte de $I_1$.
Partie B : Étude de la suite $\left(I_n\right)$
- Soit $n$ un entier naturel non nul.
- Interpréter graphiquement la quantité $I_n$.
- Émettre alors une conjecture sur le sens de variation et sur la limite éventuelle de la suite $\left(I_n\right)$. Expliciter la démarche qui a mené à cette conjecture.
-
- Justifier que, pour tout entier naturel $n$ non nul et pour tout réel $x$ appartenant à [0 ; 1], \[f_{n+1}(x) = \text{e}^{-2x}f_n(x).\]
- En déduire, pour tout entier naturel $n$ non nul et pour tout réel $x$ appartenant à [0 ; 1], \[f_{n+1}(x) \leqslant f_n(x).\]
- Déterminer alors le sens de variation de la suite $\left(I_n\right)$.
- Soit $n$ un entier naturel non nul.
- Justifier que pour tout entier naturel $n$ non nul et pour tout réel $x$ appartenant à [0 ; 1], \[0 \leqslant f_n(x) \leqslant \text{e}^{-2nx}.\]
- En déduire un encadrement de la suite $\left(I_n\right)$, puis sa limite.
Correction de l'exercice 1 (6 points)
Soit $n$ un entier naturel non nul. On considère la fonction $f_n$ définie et dérivable sur l'ensemble $\mathbb R$ des nombres réels par \[f_n(x) = x^2 \text{e}^{- 2nx}.\] On note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ dans un repère orthogonal. On définit, pour tout entier naturel $n$ non nul, $I_n = \displaystyle\int_0^1 f_n(x)\: \text{d}x$.
Partie A : Étude de la fonction $f_1$
- La fonction $f_1$ est définie sur $\mathbb R$ par $f_1(x) = x^2\text{e}^{-2x}$. On admet que $f_1$ est dérivable sur $\mathbb R$ et on note $f_1'$ sa dérivée.
- Justifier que pour tout réel $x,\: f_1'(x) = 2x\text{e}^{-2x}(1 - x)$. Pour tout réel $x$, on a $f_1′(x)=2x\text{e}^{-2x}-2x^2\text{e}^{-2x}=2x\text{e}^{-2x}(1-x)$.
- Étudier les variations de la fonction $f_1$ sur $\mathbb R$. Puisque la fonction exponentielle est strictement positive sur $\mathbb R$, le signe de $f_1(x)$ ne dépend que de celui de $x(1-x)$. Il s’agit d’un polynôme du second degré dont le coefficient principal est $a=-1$ et les racines sont $0$ et $1$.
- Déterminer la limite de $f_1$ en $- \infty$. $\lim\limits_{x \to -\infty} -2x=+\infty$ par conséquent $\lim\limits_{x \to -\infty} \text{e}^{-2x} = +\infty$.
- Vérifier que pour tout réel $x,\: f_1(x) = \left(\dfrac{x}{\text{e}^x}\right)^2$. En déduire la limite de $f_1$ en $+ \infty$. d. $f_1(x)=x^2\text{e}^{-2x}=\dfrac{x^2}{\text{e}^{2x}} = \dfrac{x^2}{\left(\text{e}^x\right)^2} = \left(\dfrac{x}{\text{e}^x}\right)^2$.
$\quad$
Par conséquent $f_1′(x)$ est négatif sur les intervalles $]-\infty;0]$ et $[1;+\infty[$ et négatif sur $[0;1]$.
Ainsi la fonction $f_1$ est décroissante sur $]-\infty;0]$, croissante sur $[0;1]$ et décroissante sur $[1;+\infty[$.
$\quad$
$\lim\limits_{x \to -\infty} x^2 = +\infty$ donc par produit $\lim\limits_{x \to -\infty} f_1(x)=+\infty$.
$\quad$
$\quad$
On sait que $\lim\limits_{x \to +\infty} \dfrac{\text{e}^x}{x}=+\infty$ donc $\lim\limits_{x \to +\infty} \dfrac{x}{\text{e}^x}=0$.
Puisque $\lim\limits_{X \to +\infty} X^2 = 0$ on obtient par composition $\lim\limits_{x \to +\infty} f_1(x)=0$.
$\quad$ - En utilisant un système de calcul formel, on trouve qu'une primitive $F_1$ de la fonction $f_1$ est donnée par $F_1(x) = - \text{e}^{-2x}\left(\dfrac{x^2}{2} + \dfrac{x}{2} + \dfrac{1}{4}\right)$. En déduire la valeur exacte de $I_1$. On a :
$\begin{align*} I_1 &= \int_0^1 f_1(x)\mathrm{d}x \\\\
&= F_1(1)-F_1(0) \\\\
&=-\text{e}^{-2} \times \dfrac{5}{4} + \dfrac{1}{4}
\end{align*}$
$\quad$
Partie B : Étude de la suite $\left(I_n\right)$
- Soit $n$ un entier naturel non nul.
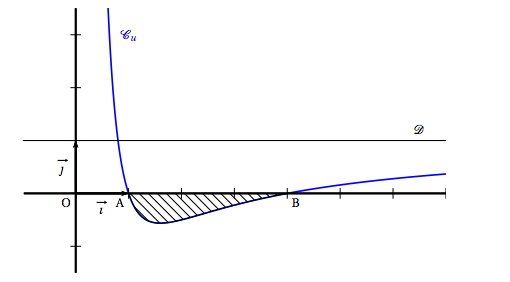
- Interpréter graphiquement la quantité $I_n$. La fonction $f_n$ est continue (car dérivable) sur $\mathbb R$ et positive sur $[0;1]$.
- Émettre alors une conjecture sur le sens de variation et sur la limite éventuelle de la suite $\left(I_n\right)$. Expliciter la démarche qui a mené à cette conjecture. On calcule des valeurs approchées de $I_n$ à l’aide de la calculatrice.
Par conséquent $I_n$ correspond à l’aire comprise entre la courbe $\mathscr{C}_n$, l’axe des abscisses et les droites d’équation $x=0$ et $x=1$.
$\quad$
$I_1 \approx 0,0808$, $I_2 \approx 0,0238$, $I_3 \approx 0,0087$, $I_4 \approx 0,0039$, $I_{100} \approx 2 \times 10^{-7}$.
La suite $\left(I_n\right)$ semble donc décroissante et converger vers $0$.
$\quad$ -
- Justifier que, pour tout entier naturel $n$ non nul et pour tout réel $x$ appartenant à [0 ; 1], \[f_{n+1}(x) = \text{e}^{-2x}f_n(x).\] Soit $n$ un entier naturel non nul.
- En déduire, pour tout entier naturel $n$ non nul et pour tout réel $x$ appartenant à [0 ; 1], \[f_{n+1}(x) \leqslant f_n(x).\] Sur $[0;1]$, la fonction $\text{e}^{-2x} \le \text{e}^0$ soit $\text{e}^{-2x} \le 1$.
- Déterminer alors le sens de variation de la suite $\left(I_n\right)$. La suite $\left(I_n\right)$ est donc décroissante.
$f_{n+1}(x)=x^2\text{e}^{-2(n+1)x} = x^2\text{e}^{-2nx-2x} = x^2\text{e}^{-2nx}\times\text{e}^{-2x}=f_n(x)\text{e}^{-2x}$
$\quad$
Par conséquent, en multipliant les deux côtés de cette inégalité par $f_n(x)$, qui est toujours positif sur $[0;1]$ car produit de facteurs positifs, on obtient :
$f_{n+1}(x) = f_n(x)\text{e}^{-2x} \le f_n(x)$.
$\quad$
- Soit $n$ un entier naturel non nul.
- Justifier que pour tout entier naturel $n$ non nul et pour tout réel $x$ appartenant à [0 ; 1], \[0 \leqslant f_n(x) \leqslant \text{e}^{-2nx}.\] Sur $[0;1]$, $0 \le x^2 \le 1$.
- En déduire un encadrement de la suite $\left(I_n\right)$, puis sa limite. On a donc, en intégrant sur $[0;1]$ :
Par conséquent, en multipliant l’encadrement par $\text{e}^{-2nx}$ qui est toujours positif, on obtient $0 \le f_n(x) \le \text{e}^{-2nx}$ pour tout entier naturel $n$ non nul.
$\quad$
$\begin{align*} 0 \le I_n \le \int_0^1 \text{e}^{-2nx}\mathrm{d}x &\Leftrightarrow 0 \le I_n \le \left[\dfrac{\text{e}^{-2nx}}{-2n}\right]_0^1 \\\\
&\Leftrightarrow 0 \le I_n \le \dfrac{\text{e}^{-2n}}{-2n}+\dfrac{1}{2n}
\end{align*}$
Or $\lim\limits_{n \to +\infty} \dfrac{1}{2n}=0$, $\lim\limits_{n \to +\infty} \text{e}^{-2n} = 0$ donc $\lim\limits_{n \to +\infty} \dfrac{\text{e}^{-2n}}{-2n} = 0$.
Par conséquent $\lim\limits_{n \to +\infty} \left(\dfrac{\text{e}^{-2n}}{-2n}+\dfrac{1}{2n}\right) = 0$
D’après le théorème des gendarmes, on a donc $\lim\limits_{n \to +\infty} I_n =0$.
$\quad$
Exercice 2 5 points
Dans un supermarché, on réalise une étude sur la vente de bouteilles de jus de fruits sur une période d'un mois.
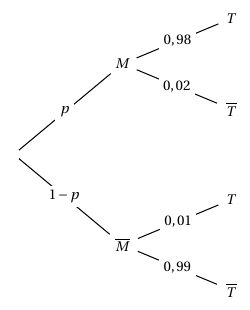
- 40% des bouteilles vendues sont des bouteilles de jus d'orange ;
- 25% des bouteilles de jus d'orange vendues possèdent l'appellation « pur jus ».
Parmi les bouteilles qui ne sont pas de jus d'orange, la proportion des bouteilles de « pur jus » est notée $x$, où $x$ est un réel de l'intervalle [0 ; 1]. Par ailleurs, 20% des bouteilles de jus de fruits vendues possèdent l'appellation « pur jus ».
On prélève au hasard une bouteille de jus de fruits passée en caisse.
On définit les évènements suivants :
$R$ : la bouteille prélevée est une bouteille de jus d'orange ;
$J$ : la bouteille prélevée est une bouteille de « pur jus ».
Partie A
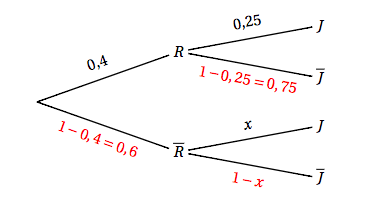
- Représenter cette situation à l'aide d'un arbre pondéré.
- Déterminer la valeur exacte de $x$.
- Une bouteille passée en caisse et prélevée au hasard est une bouteille de « pur jus ». Calculer la probabilité que ce soit une bouteille de jus d'orange.
Partie B
Afin d'avoir une meilleure connaissance de sa clientèle, le directeur du supermarché fait une étude sur un lot des $500$ dernières bouteilles de jus de fruits vendues.
On note $X$ la variable aléatoire égale au nombre de bouteilles de « pur jus » dans ce lot.
On admettra que le stock de bouteilles présentes dans le supermarché est suffisamment important pour que le choix de ces $500$ bouteilles puisse être assimilé à un tirage au sort avec remise.
- Déterminer la loi suivie par la variable aléatoire $X$. On en donnera les paramètres.
- Déterminer la probabilité pour qu'au moins 75 bouteilles de cet échantillon de $500$ bouteilles soient de « pur jus ». On arrondira le résultat au millième.
Partie C
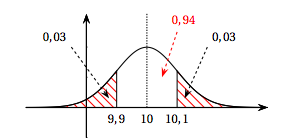
Un fournisseur assure que 90% des bouteilles de sa production de pur jus d'orange contiennent moins de 2% de pulpe. Le service qualité du supermarché prélève un échantillon de 900 bouteilles afin de vérifier cette affirmation. Sur cet échantillon, $766$ bouteilles présentent moins de 2% de pulpe.
- Déterminer l'intervalle de fluctuation asymptotique de la proportion de bouteilles contenant moins de 2% de pulpe au seuil de 95%.
- Que penser de l'affirmation du fournisseur ?
Correction de l'exercice 2 (5 points)
Dans un supermarché, on réalise une étude sur la vente de bouteilles de jus de fruits sur une période d'un mois.
- 40% des bouteilles vendues sont des bouteilles de jus d'orange ;
- 25% des bouteilles de jus d'orange vendues possèdent l'appellation « pur jus ».
Parmi les bouteilles qui ne sont pas de jus d'orange, la proportion des bouteilles de « pur jus » est notée $x$, où $x$ est un réel de l'intervalle [0 ; 1]. Par ailleurs, 20% des bouteilles de jus de fruits vendues possèdent l'appellation « pur jus ».
On prélève au hasard une bouteille de jus de fruits passée en caisse.
On définit les évènements suivants :
$R$ : la bouteille prélevée est une bouteille de jus d'orange ;
$J$ : la bouteille prélevée est une bouteille de « pur jus ».
Partie A
- Représenter cette situation à l'aide d'un arbre pondéré.
- Déterminer la valeur exacte de $x$. D’après la formule des probabilités totales on a :
- Une bouteille passée en caisse et prélevée au hasard est une bouteille de « pur jus ». Calculer la probabilité que ce soit une bouteille de jus d'orange. On veut calculer :
$\begin{align*} \phantom{\Leftrightarrow }p(J) &=p(R \cap J)+p\left(\overline{R} \cap J\right) \\\\
\Leftrightarrow 0,2&=0,4 \times 0,25 + 0,6x \\\\
\Leftrightarrow 0,1&=0,6x\\\\
\Leftrightarrow x&=\dfrac{1}{6}
\end{align*}$
$\quad$
$\begin{align*} p_J(R)&=\dfrac{p(J\cap R)}{p(J)} \\\\
&=\dfrac{0,4 \times 0,25}{0,2} \\\\
&=\dfrac{1}{2}
\end{align*}$
$\quad$
Partie B
Afin d'avoir une meilleure connaissance de sa clientèle, le directeur du supermarché fait une étude sur un lot des $500$ dernières bouteilles de jus de fruits vendues.
On note $X$ la variable aléatoire égale au nombre de bouteilles de « pur jus » dans ce lot.
On admettra que le stock de bouteilles présentes dans le supermarché est suffisamment important pour que le choix de ces $500$ bouteilles puisse être assimilé à un tirage au sort avec remise.
- Déterminer la loi suivie par la variable aléatoire $X$. On en donnera les paramètres. Il s’agit de $500$ tirages indépendants, avec remise, aléatoires ne présentant que deux issues : $J$ et $\overline{J}$. De plus $p(J)=0,2$.
- Déterminer la probabilité pour qu'au moins 75 bouteilles de cet échantillon de $500$ bouteilles soient de « pur jus ». On arrondira le résultat au millième. On veut calculer $P(X\ge 75) = 1-P(X \le 74) \approx 0,998$
La variable aléatoire $X$ suit donc la loi binomiale de paramètres $n=500$ et $p=0,2$.
$\quad$
La probabilité qu’au moins $75$ bouteilles de cet échantillon soient pur jus est donc d’environ $99,8\%$.
$\quad$
Partie C
Un fournisseur assure que 90% des bouteilles de sa production de pur jus d'orange contiennent moins de 2% de pulpe. Le service qualité du supermarché prélève un échantillon de 900 bouteilles afin de vérifier cette affirmation. Sur cet échantillon, $766$ bouteilles présentent moins de 2% de pulpe.
- Déterminer l'intervalle de fluctuation asymptotique de la proportion de bouteilles contenant moins de 2% de pulpe au seuil de 95%. On a $n=900$ et $p=0,9$
- Que penser de l'affirmation du fournisseur ? La fréquence observée est $f=\dfrac{766}{900} \approx 0,851 \notin I_{900}$.
Ainsi $n = 900 \ge 30 \checkmark$ $\quad np=810 \ge 5 \checkmark$ $\quad n(1-p) = 90 \ge 5 \checkmark$.
Un intervalle de fluctuation asymptotique au seuil de $95\%$ est donc :
$\begin{align*} I_{900} &=\left[0,9-1,96\sqrt{\dfrac{0,9 \times 0,1}{900}};0,9+1,96\sqrt{\dfrac{0,9 \times 0,1}{900}}\right] \\\\
& =[0,8804;0,9196]
\end{align*}$
$\quad$
Par conséquent, au risque de $5\%$ on peut remettre en question l’affirmation du fournisseur.
$\quad$
Exercice 3 4 points
Les trois questions sont indépendantes. Toute réponse doit être justifiée.
- On définit une suite $\left(u_n\right)$ de réels strictement positifs par \[u_0 = 1\quad \text{et pour tout entier naturel } \:n,\quad \ln \left(u_{n+1}\right) = \ln \left(u_{n}\right) - 1.\]
La suite $\left(u_n\right)$ est-elle géométrique ? - Soit $\left(v_n\right)$ une suite à termes strictement positifs. On définit la suite $\left(w_n\right)$ par, pour tout entier naturel $n,\: w_n = 1 - \ln \left(v_{n}\right)$.
La proposition $(\mathcal{P})$ suivante est-elle vraie ou fausse ?
\[(\mathcal{P}) : \text{si la suite }\:\left(v_{n}\right)\: \text{est majorée alors la suite }\:\left(w_{n}\right)\: \text{est majorée.}\] - La suite $\left(z_{n}\right)$ de nombres complexes est définie par \[z_0 = 2 + 3\text{i}\: \text{ et, pour tout entier naturel }\:n \:\:\text{par}\: z_{n+1} = \left(\dfrac{\sqrt{2}}{4} + \text{i}\dfrac{\sqrt{6}}{4} \right)z_n.\] Pour quelles valeurs de $n$,$\left|z_n\right|$ est-il inférieur ou égal à $10^{-20}$ ?
Exercice 3 4 points
Les trois questions sont indépendantes. Toute réponse doit être justifiée.
- On définit une suite $\left(u_n\right)$ de réels strictement positifs par \[u_0 = 1\quad \text{et pour tout entier naturel } \:n,\quad \ln \left(u_{n+1}\right) = \ln \left(u_{n}\right) - 1.\]
La suite $\left(u_n\right)$ est-elle géométrique ? On a $\ln\left(u_{n+1}\right) = \ln \left(u_n\right) -1 = \ln \dfrac{u_n}{\text{ e}}$. - Soit $\left(v_n\right)$ une suite à termes strictement positifs. On définit la suite $\left(w_n\right)$ par, pour tout entier naturel $n,\: w_n = 1 - \ln \left(v_{n}\right)$.
La proposition $(\mathcal{P})$ suivante est-elle vraie ou fausse ?
\[(\mathcal{P}) : \text{si la suite }\:\left(v_{n}\right)\: \text{est majorée alors la suite }\:\left(w_{n}\right)\: \text{ est majorée.}\] Prenons par exemple la suite $\left(v_n\right)$ définie par $v_n=\text{ e}^{-n}$. - La suite $\left(z_{n}\right)$ de nombres complexes est définie par \[z_0 = 2 + 3\text{i} \text{ et, pour tout entier naturel }\:n \text{par}\: z_{n+1} = \left(\dfrac{\sqrt{2}}{4} + \text{i}\dfrac{\sqrt{6}}{4} \right)z_n.\] Pour quelles valeurs de $n$,$\left|z_n\right|$ est-il inférieur ou égal à $10^{-20}$ ? $\left|\dfrac{\sqrt{2}}{4}+\text{ i}\dfrac{\sqrt{6}}{4}\right|=\sqrt{\dfrac{1}{2}}=\dfrac{\sqrt{2}}{2}$
Cela signifie donc que $u_{n+1}=\dfrac{u_n}{\text{ e}}$.
La suite $\left(u_n\right)$ est donc géométrique de raison $\dfrac{1}{\text{ e}}$ et de premier terme $u_0=1$.
$\quad$
Pour tout entier naturel $n$, on a $v_n \le 1$. La suite $\left(v_n\right)$ est donc majorée.
$w_n=1-\ln\left(v_n\right)=1-\ln \text{ e}^{-n} = 1-(-n)=1+n$.
La suite $\left(w_n\right)$ n’est donc pas majorée.
La proposition est donc fausse.
$\quad$
On a donc $\left|z_{n+1}\right|=\dfrac{\sqrt{2}}{2}\left|z_n\right|$.
La suite $\left(\left|z_n\right|\right)$ est donc géométrique de raison $\dfrac{\sqrt{2}}{2}$
Son premier terme est $\left|z_0\right| = \sqrt{13}$.
Ainsi, pour tout entier naturel $n$, on a $\left|z_n\right|=\sqrt{13}\times \left(\dfrac{\sqrt{2}}{2}\right)^n$.
On cherche la plus petite valeur de $n$ telle que :
$\begin{align*} \sqrt{13}\times \left(\dfrac{\sqrt{2}}{2}\right)^n \le 10^{-20} &\Leftrightarrow \left(\dfrac{\sqrt{2}}{2}\right)^n \le \dfrac{10^{-20}}{\sqrt{13}} \\\\
&\Leftrightarrow n\ln \dfrac{\sqrt{2}}{2} \le \ln \dfrac{10^{-20}}{\sqrt{13}} \\\\
&\Leftrightarrow n \ge \dfrac{\ln \dfrac{10^{-20}}{\sqrt{13}}}{\ln \dfrac{\sqrt{2}}{2}} \\\\
&\Leftrightarrow 137
\end{align*}$
Par conséquent, pour tout entier naturel supérieur ou égal à $137$, $\left|z_n\right|\le 10^{20}$.
$\quad$
Exercice 4 5 points
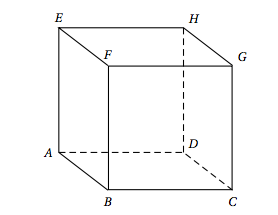
Soit ABCDEFGH le cube ci-dessous.
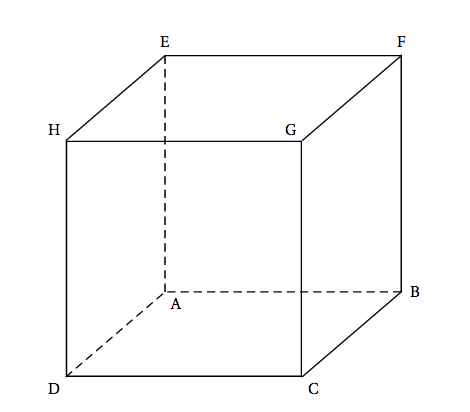
On se place dans le repère orthonormé $\left(A~;~\vec{\text{AB}},\: \vec{\text{AD}},\: \vec{\text{AE}}\right)$.
-
- Montrer que la droite (DB) admet pour représentation paramétrique \[\left\{\begin{array}{l c l} x &=& \phantom{1 -}s\\ y &=& 1 - s ,\\ z &=& \phantom{1 -}0 \end{array}\right.,\: \text{où s décrit l'ensemble } \mathbb R\: \text{des nombres réels}.\]
- Montrer que les points de la droite (AG) sont les points de coordonnées $(t~;~t~;~t)$ où $t$ est un réel.
- Soit $M$ un point quelconque de la droite (DB) et $N$ un point quelconque de la droite (AG). Démontrer que la droite $(MN)$ est perpendiculaire aux deux droites (AG) et (DB) si et seulement si $M$ et $N$ ont pour coordonnées respectives $\left(\frac{1}{2}~;~\frac{1}{2}~;~0\right)$ et $\left(\frac{1}{3}~;~\frac{1}{3}~;~\frac{1}{3}\right)$.
- Soit $s$ et $t$ deux réels quelconques. On note $M(s~;~1 - s~;~0)$ un point de la droite (DB) et $N(t~;~t~;~t)$ un point de la droite (AG).
- Montrer que $MN^2 = 3 \left(t - \frac{1}{3}\right)^2 + 2\left(s - \frac{1}{2}\right)^2 + \frac{1}{6}$.
- En déduire la position des points $M$ et $N$ pour laquelle la distance $MN$ est minimale. Que peut-on dire de la droite $(MN)$ dans ce cas ?
Correction de l'exercice 4 5 points
Soit ABCDEFGH le cube ci-dessous.

On se place dans le repère orthonormé $\left(A~;~\vec{\text{AB}},\: \vec{\text{AD}},\: \vec{\text{AE}}\right)$.
-
- Montrer que la droite (DB) admet pour représentation paramétrique \[\left\{\begin{array}{l c l} x &=& \phantom{1 -}s\\ y &=& 1 - s ,\\ z &=& \phantom{1 -}0 \end{array}\right.,\: \text{où s décrit l'ensemble } \mathbb R\: \text{des nombres réels}.\] On a $B(1;0;0)$ et $D(0;1;0)$.
- Montrer que les points de la droite (AG) sont les points de coordonnées $(t~;~t~;~t)$ où $t$ est un réel. On a $A(0;0;0)$ et $G(1;1;1)$.
En prenant $s=1$ dans la représentation paramétrique fournie, on retrouve les coordonnées de $B$.
En prenant $s=0$ dans la représentation paramétrique fournie, on retrouve les coordonnées de $D$.
Il s’agit donc bien d’une représentation paramétrique de la droite $(DB)$.
$\quad$
Ainsi $\overrightarrow{AG}(1;1;1)$
Une représentation paramétrique de $(AG)$ est par conséquent $\begin{cases}x=t\\y=t \quad t\in \mathbb R\\z=t\end{cases}$.
Les points de la droite $(AG)$ sont donc bien les points de coordonnées $(t;t;t)$ où $t$ est un réel.
$\quad$ - Soit $M$ un point quelconque de la droite (DB) et $N$ un point quelconque de la droite (AG). Démontrer que la droite $(MN)$ est perpendiculaire aux deux droites (AG) et (DB) si et seulement si $M$ et $N$ ont pour coordonnées respectives $\left(\frac{1}{2}~;~\frac{1}{2}~;~0\right)$ et $\left(\frac{1}{3}~;~\frac{1}{3}~;~\frac{1}{3}\right)$. On a $M(s;1-s;0)$ et $N(t;t;t)$. Ainsi $\overrightarrow{MN}(t-s;t+s-1;t)$.
- Soit $s$ et $t$ deux réels quelconques. On note $M(s~;~1 - s~;~0)$ un point de la droite (DB) et $N(t~;~t~;~t)$ un point de la droite (AG).
- Montrer que $MN^2 = 3 \left(t - \frac{1}{3}\right)^2 + 2\left(s - \frac{1}{2}\right)^2 + \frac{1}{6}$.
- En déduire la position des points $M$ et $N$ pour laquelle la distance $MN$ est minimale. Que peut-on dire de la droite $(MN)$ dans ce cas ? On a donc $MN^2 \ge \dfrac{1}{6}$ et $MN^2 = \dfrac{1}{6}$ si, et seulement si, $t=\dfrac{1}{3}$ et $s=\dfrac{1}{2}$.
$\begin{align*} MN^2&=(t-s)^2+(t+s-1)^2+t^2\\\\
&=t^2-2st+s^2+t^2+2ts-2t+s^2-2s+1+t^2 \\\\
&=3t^2-2t+2s^2-2s+1 \\\\
&=3\left(t^2-\dfrac{2}{3}t\right) + 2(s^2-s)+1 \\\\
&=3\left(t-\dfrac{1}{3}\right)^2-\dfrac{1}{3}+ 2\left(s-\dfrac{1}{2}\right)^2-\dfrac{1}{2}+1 \\\\
&=3\left(t-\dfrac{1}{3}\right)^2+ 2\left(s-\dfrac{1}{2}\right)^2+\dfrac{1}{6}
\end{align*}$
$\quad$
La droite $(MN)$ est alors perpendiculaire aux droites $(AG)$ et $(DB)$.
$\quad$
$\overrightarrow{AG}.\overrightarrow{MN} = t-s+t+s-1+t = 3t-1$ et $\overrightarrow{DB}.\overrightarrow{MN} = t-s-(t+s-1) = -2s+1$
$\quad$
$(MN)$ est perpendiculaire à $(AG)$ et $(DB)$
si, et seulement si, $\overrightarrow{AG}.\overrightarrow{MN} =0$ et $\overrightarrow{DB}.\overrightarrow{MN} = 0$
si, et seulement si, $3t-1=0$ et $-2s+1=0$
si, et seulement si, $t=\dfrac{1}{3}$ et $s=\dfrac{1}{2}$
si, et seulement si, $M\left(\dfrac{1}{2};\dfrac{1}{2};0\right)$ et $N\left(\dfrac{1}{3};\dfrac{1}{3};\dfrac{1}{3}\right)$
$\quad$
Spécialité 5 points
Partie A
On considère l'équation \[51x - 26y = 1\] où $x$ et $y$ sont des nombres entiers relatifs.
- Justifier, en énonçant un théorème du cours, que cette équation admet au moins un couple solution.
-
- Donner un couple solution $\left(x_0~;~y_0\right)$ de cette équation.
- Déterminer l'ensemble des couples solutions de cette équation.
Partie B
On fait correspondre à chaque lettre de l'alphabet un nombre entier comme l'indique le tableau ci-dessous : $$\begin{array}{{|c|c|c|c|c|c|c|c|c|c|c|c|c|}}\hline A &B&C &D&E &F&G &H&I&J& K &L &M \\ \hline 0 &1 &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12\\ \hline \hline N &O &P &Q &R &S & T &U &V &W &X &Y &Z\\ \hline 13 &14 &15 &16 &17 &18 &19 &20 &21 &22 &23 &24 &25\\ \hline \end{array} $$ Afin de coder une lettre de l'alphabet, correspondant à un entier $x$ compris entre $0$ et $25$, on définit une fonction de codage $f$ par $f(x) = y$, où $y$ est le reste de la division euclidienne de $51x + 2$ par $26$. La lettre de l'alphabet correspondant à l'entier $x$ est ainsi codée par la lettre correspondant à l'entier $y$.
- Coder la lettre N.
- En utilisant la partie A, déterminer l'entier $a$ tel que $0 \leqslant a \leqslant 25$ et $51a \equiv 1\:\:[26]$.
- Démontrer que si la lettre correspondant à un entier $x$ est codée par une lettre correspondant à un entier $y$, alors $x$ est le reste de la division euclidienne de $ay + 2$ par $26$.
- Déterminer alors la lettre qui est codée par la lettre N.
- On applique $100$ fois de suite la fonction de codage $f$ à un nombre $x$ correspondant à une certaine lettre. Quelle lettre obtient-on ?
Correction de l'exercice de Spécialité 5 points
Partie A
On considère l'équation \[51x - 26y = 1\] où $x$ et $y$ sont des nombres entiers relatifs.
- Justifier, en énonçant un théorème du cours, que cette équation admet au moins un couple solution. Les nombres $51$ et $26$ sont premiers entre eux.
-
- Donner un couple solution $\left(x_0~;~y_0\right)$ de cette équation. $51 \times (-1)-26\times (-2) = -51+52=1$
- Déterminer l'ensemble des couples solutions de cette équation. Soit $(x;y)$ une autre solution de cette équation.
Le couple $(-1;-1)$ est donc solution de cette équation.
$\quad$
$51x-26y=1$ et $51 \times (-1)-26\times (-2) =1$
Par différence, on obtient :
$51(x+1)-26(y+2)=0$ soit $51(x+1)=26(y+2)$
Les nombres $51$ et $26$ sont premiers entre eux.
D’après le théorème de Gauss, il existe donc un entier relatif $k$ tel que $x+1=26k$ et $y+2=51k$
Soit $x=26k-1$ et $y=51k-2$.
$\quad$
Réciproquement :
Soit $k$ un entier relatif.
$51(26k-1)-26(51k-2)=1326k-51-1326k+52=1$
L’ensemble des couples solutions de l’équation est donc l’ensemble des couples $(26k-1;51k-2)$ pour tout entier relatif $k$.
$\quad$
D’après le théorème de Bezout, l’équation $51x-26y=1$ admet donc au moins une solution.
$\quad$
Partie B
On fait correspondre à chaque lettre de l'alphabet un nombre entier comme l'indique le tableau ci-dessous : $$\begin{array}{{|c|c|c|c|c|c|c|c|c|c|c|c|c|}}\hline A &B&C &D&E &F&G &H&I&J& K &L &M \\ \hline 0 &1 &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12\\ \hline \hline N &O &P &Q &R &S & T &U &V &W &X &Y &Z\\ \hline 13 &14 &15 &16 &17 &18 &19 &20 &21 &22 &23 &24 &25\\ \hline \end{array} $$ Afin de coder une lettre de l'alphabet, correspondant à un entier $x$ compris entre $0$ et $25$, on définit une fonction de codage $f$ par $f(x) = y$, où $y$ est le reste de la division euclidienne de $51x + 2$ par $26$. La lettre de l'alphabet correspondant à l'entier $x$ est ainsi codée par la lettre correspondant à l'entier $y$.
- Coder la lettre N. $N$ est associé à l’entier $13$.
- En utilisant la partie A, déterminer l'entier $a$ tel que $0 \leqslant a \leqslant 25$ et $51a \equiv 1\:\:[26]$. $51a\equiv 1~[26]$ Il existe donc un entier relatif $b$ tel que $51a=1+26b$ soit $51a-26b=1$
- Démontrer que si la lettre correspondant à un entier $x$ est codée par une lettre correspondant à un entier $y$, alors $x$ est le reste de la division euclidienne de $ay + 2$ par $26$. On a donc :
- Déterminer alors la lettre qui est codée par la lettre N. $25 \times 13 + 2=327 \equiv 15~[26]$
- On applique $100$ fois de suite la fonction de codage $f$ à un nombre $x$ correspondant à une certaine lettre. Quelle lettre obtient-on ? Si $f(x)=y$ alors
$51\times 13 + 2=665$ et $665\equiv 15~[26]$
$N$ est donc codé par la lettre $P$.
$\quad$
D’après la partie A, il existe donc un entier relatif $k$ tel que $a=26k-1$.
On veut que $0 \le a \le 26$ $\Leftrightarrow 0 \le 26k-1\le 1$ $\Leftrightarrow 1\le 26k \le 27$ $\Leftrightarrow k=1$
Par conséquent $a=25$.
$\quad$
$\begin{align*} 51x+2\equiv y~[26] & \rightarrow 51ax+2a \equiv ay~[26] \\\\
&\rightarrow x+50 \equiv ay~[26] \\\\
&\rightarrow x+24 \equiv ay~[26] \\\\
&\rightarrow x \equiv ay-26~[26] \\\\
&\rightarrow x\equiv ay+2~[26]
\end{align*}$
$\quad$
Ainsi la lettre $P$ est codée par la lettre $N$.
$\quad$
$51y+2 \equiv 25y+2~[26]$ soit $f(y)=x$.
Ainsi $f\left(f(x)\right)=x$
Quand on applique deux fois de suite la fonction $f$ on retrouve la lettre de départ.
Par conséquent si on applique $100$ fois de suite la fonction $f$ on obtiendra la lettre de départ.
$\quad$
- Vues: 36585

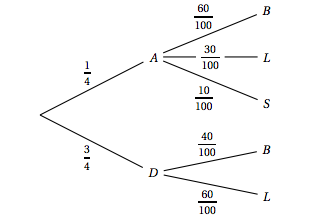
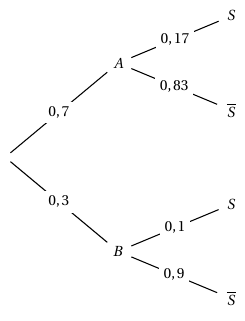
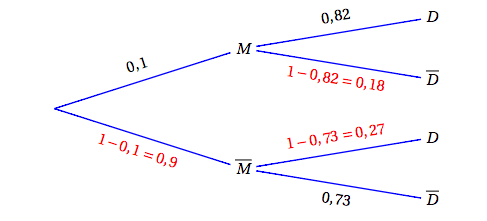 D’après la formule des probabilités totales, on a alors :
D’après la formule des probabilités totales, on a alors :