Baccalauréat S Antilles Guyane19 juin 2018 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Un publicitaire souhaite imprimer le logo ci-dessous sur un T-shirt:

Il dessine ce logo à l'aide des courbes de deux fonctions $f$ et $g$ définies sur $\mathbb R$ par: \[ f(x)=\text{e}^{-x}(-\cos x+\sin x+1)\text{ et } g(x)=-\text{e}^{-x}\cos x. \] On admet que les fonctions $f$ et $g$ sont dérivables sur $\mathbb R$.

Partie A — Étude de la fonction $f$

 

1. Justifier que, pour tout $x\in\mathbb R$:\[ -\text{e}^{-x}\leqslant f(x)\leqslant 3\text{e}^{-x}.\]
Pour tout réel $x$ on a $-1 \leqslant \cos x \leqslant 1$ donc $-1\leqslant -\cos x \leqslant 1$
et $-1\leqslant \sin x \leqslant 1$
Ainsi $-1-1+1 \leqslant -\cos x+\sin x+1 \leqslant 1+1+1 \iff -1\leqslant -\cos x+\sin x+1 \leqslant 3$
La fonction exponentielle étant strictement positive sur $\mathbb R$.
On a alors $-\text{e}^{-x} \leqslant f(x) \leqslant 3\text{e}^{-x}$.
$\quad$
2. En déduire la limite de $f$ en $+\infty$.
$\lim\limits_{x \to +\infty} -x=-\infty$ et $\lim\limits_{t \to -\infty} \text{e}^t=0$.
Donc $\lim\limits_{x \to +\infty} \text{e}^{-x}=0$.
Par conséquent $\lim\limits_{x \to +\infty}-\text{e}^{-x}=0$ et $\lim\limits_{x \to +\infty} 3\text{e}^{-x}=0$.
D’après le théorème des gendarmes $\lim\limits_{x \to +\infty} f(x)=0$.
$\quad$
3. Démontrer que, pour tout $x\in\mathbb R$, $f'(x)=\text{e}^{-x}(2\cos x-1)$ où $f'$ est la fonction dérivée de $f$.
La fonction $f$ est dérivable sur $\mathbb R$ en tant que somme et produit de fonctions dérivables sur $\mathbb R$.
Pour tout réel $x$ on a :
$\begin{align*} f'(x)&=-\text{e}^{-x}\left(-\cos x+\sin x+1\right)+\text{e}^{-x}\left(-(-\sin x)+\cos x\right) \\
&=\left(\cos x-\sin x-1+\sin x+\cos x\right)\text{e}^{-x} \\
&=\left(2\cos x-1\right)\text{e}^{-x}
\end{align*}$
$\quad$
4. Dans cette question, on étudie la fonction $f$ sur l'intervalle $[-\pi;\pi]$.
   1. Déterminer le signe de $f'(x)$ pour $x$ appartenant à l'intervalle $[-\pi;\pi]$.
   La fonction exponentielle est strictement positive sur $[-\pi;\pi]$.
   Le signe de $f'(x)$ ne dépend donc que de celui de $2\cos x-1$.
   Or, sur l’intervalle $[-\pi;\pi]$ :
   $2\cos x-1=0 \\ \iff \cos x =0,5 \\ \iff \begin{cases} x=\dfrac{\pi}{3}\\\text{ou}\\x=-\dfrac{\pi}{3}\end{cases}$
   et $2\cos x-1>0 \\ \iff \cos x>0,5 \\ \iff x \in \left]-\dfrac{\pi}{3};\dfrac{\pi}{3}\right[$.
   Ainsi sur l’intervalle $[-\pi;\pi]$, $f'(x)<0$ sur $\left]-\pi;-\dfrac{\pi}{3}\right[\cup\left]\dfrac{\pi}{3};\pi\right]$.
   $\quad$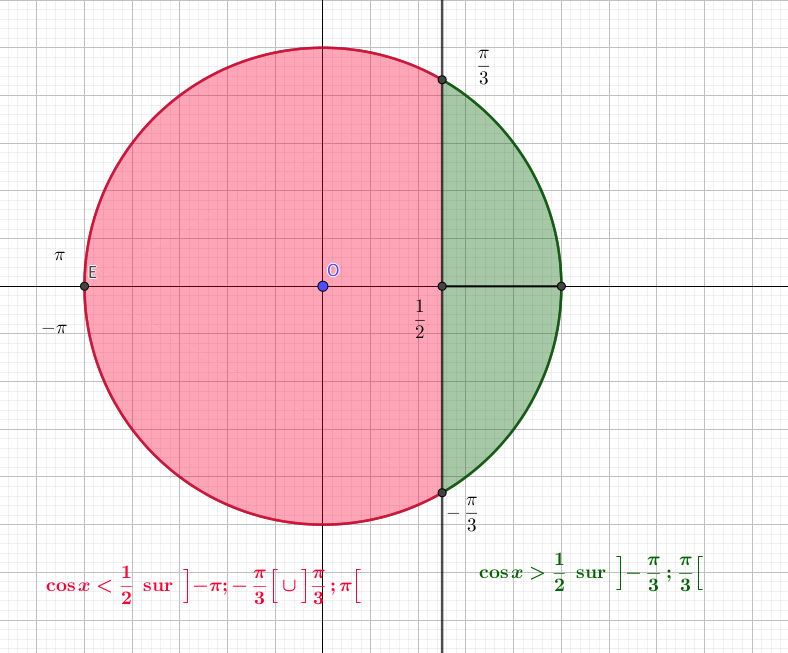
   
   
   2. En déduire les variations de $f$ sur $[-\pi;\pi]$.
   La fonction $f$ est donc décroissante sur les intervalles $\left]-\pi;-\dfrac{\pi}{3}\right[$ et $\left]\dfrac{\pi}{3};\pi\right]$ et elle est croissante sur l’intervalle $\left]-\dfrac{\pi}{3};\dfrac{\pi}{3}\right[$.
   $\quad$

 

Partie B — Aire du logo

On note $\mathcal{C}_f$ et $\mathcal{C}_g$ les représentations graphiques des fonctions $f$ et $g$ dans un repère orthonormé $\left(\text{O}~;~\vec{\imath},~\vec{\jmath}\right)$. L'unité graphique est de 2 centimètres. Ces deux courbes sont tracées en ANNEXE.

1. Étudier la position relative dela courbe $\mathcal{C}_f$ par rapport à la courbre $\mathcal{C}_g$ sur $\mathbb R$.
Pour tout réel $x$ on a : $f(x)-g(x)=\text{e}^{-x}\left(\sin x+1\right)$.
Or $-1\leqslant \sin x\leqslant 1$ donc $0\leqslant \sin x +1 \leqslant 2$.
Puisque la fonction exponentielle est strictement positive sur$mathbb R$, cela signifie donc que $f(x)-g(x) \geqslant 0$.
La courbe $\mathscr{C}_f$ est par conséquent toujours au-dessus de la courbe $\mathscr{C}_g$.

2. Soit $H$ la fonction définie sur $\mathbb R$ par: \[ H(x)=\left(-\frac{\cos x}{2}-\frac{\sin x}{2}-1\right)\text{e}^{-x}. \] On admet que $H$ est une primitive de la fonction $x\mapsto (\sin x+1)\text{e}^{-x}$ sur $\mathbb R$ . On note $\mathcal{D}$ le domaine délimité par la courbe $\mathcal{C}_f$, la courbe $\mathcal{C}_g$ est les droites d'équation $x=-\frac{\pi}{2}$ et $x=\frac{3\pi}{2}$.
   1. Hachurer le domaine $\mathcal{D}$ sur le graphique en annexe à rendre avec la copie.
   
   2. Calculer, une unité d'aire, l'aire du domaine $\mathcal{D}$, puis en donner une valeur approchée à $10^{-2}$ près en cm$^{2}$.
   La fonction $h$ définie sur $\mathbb R$ par $ h(x)=f(x)-g(x)$ est positive (question B.1) et continue (somme de fonctions continues sur $\mathbb R$).
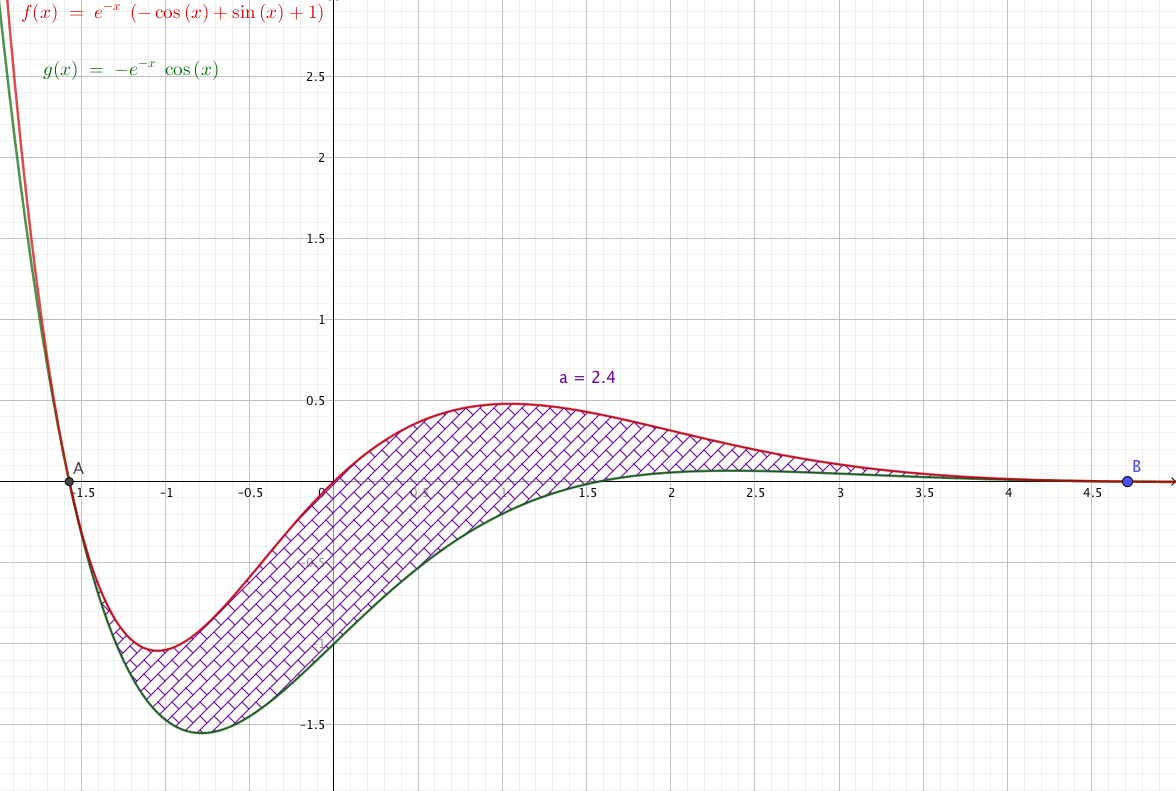
   Par conséquent l’aire du domaine $\mathcal{D}$ est :
   $\begin{align*} \displaystyle \mathscr{A}&=\int_{-\frac{\pi}{2}}^{\frac{3\pi}{2}} \left(f(x)-g(x)\right) \text{d}x \\
   &=H\left(\dfrac{3\pi}{2}\right)-H\left(-\dfrac{\pi}{2}\right) \\
   &=\left(\dfrac{1}{2}-1\right)\text{e}^{-3\pi/2}-\left(\dfrac{1}{2}-1\right)\text{e}^{\pi/2} \\
   &=-\dfrac{1}{2}\text{e}^{-3\pi/2}+\dfrac{1}{2}\text{e}^{\pi/2} \text{ u.a.}
   \end{align*}$
   Or $1$ u.a. $=2^2=4$ cm$^2$.
   Ainsi $\mathscr{A}\approx 9,60$ cm$^2$.
   $\quad$