Baccalauréat S Antilles Guyane19 juin 2018 - Exercice 2

Page 3 sur 10: Exercice 2

Exercice 2 5 points

Commun à tous les candidats

Un artiste souhaite réaliser une sculpture composée d'un tétraèdre posé sur un cube de 6 mètres d'arête. Ces deux solides sont représentés par le cube $ABCDEFGH$ et par le tétraèdre $SELM$ ci-dessous.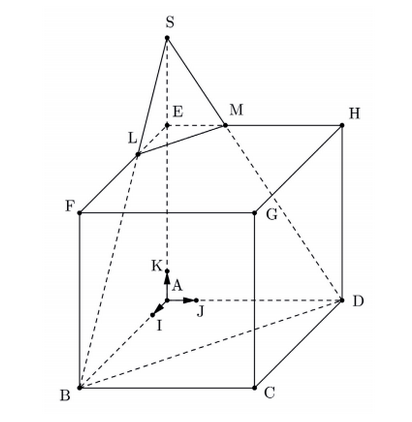

On munit l'espace du repère orthonormé $\left(A;\vec{AI},\vec{AJ},\vec{AK}\right)$ tel que: $I\in[AB]$, $J\in[AD]$, $K\in[AE]$ et $AI=AJ=AK=1$, l'unité graphique représentant 1 mètre. Les points $L$, $M$ et $S$ sont définis de la façon suivante:

• $L$ est le point tel que $\vec{FL}=\frac23\vec{FE}$;
• $M$ est le point d'intersection du plan $(BDL)$ et de la droite $(EH)$;
• $S$ est le point d'intersection des droites $(BL)$ et $(AK)$.

1. Démontrer, sans calcul de coordonnées, que les droites $(LM)$ et $(BD)$ sont parallèles.
2. Démontrer que les coordonnées du point $L$ sont $(2~;~0~;~6)$.
3. 1. Donner une représentation paramétrique de la droite $(BL)$.
   2. Vérifier que les coordonnées du point $S$ sont $(0~;~0~;~9)$.
4. Soit $\vec{n}$ le vecteur de coordonnées $(3~;~3~;~2)$.
   1. Vérifier que $\vec{n}$ est normal au plan $(BDL)$.
   2. Démontrer qu'une équation cartésienne du plan $(BDL)$ est: \[ 3x+3y+2z-18=0. \]
   3. On admet que la droite $(EH)$ a pour représentation paramétrique: \[ \left\{ \begin{array}{rcl} x&=&0\\ y&=&s~~~~(s\in\mathbb R)\\ z&=&6 \end{array} \right. \] Calculer les coordonnées du point $M$.
5. Calculer le volume du tétraèdre $SELM$. On rappelle que le volume $V$ d'un tétraèdre est donné par la formule suivante: \[ V=\frac13\times\text{Aire de la base}\times\text{Hauteur}. \]
6. L'artiste souhaite que la mesure de l'angle $\widehat{SLE}$ soit comprise entre 55$^{o}$ et 60$^{o}$.
   Cette contrainte d'angle est-elle respectée ?