Baccalauréat S Antilles Guyane19 juin 2018 - Correction Exercice 2
Page 4 sur 10
Correction de l'exercice 2 (5 points)
Un artiste souhaite réaliser une sculpture composée d'un tétraèdre posé sur un cube de 6 mètres d'arête. Ces deux solides sont représentés par le cube $ABCDEFGH$ et par le tétraèdre $SELM$ ci-dessous. 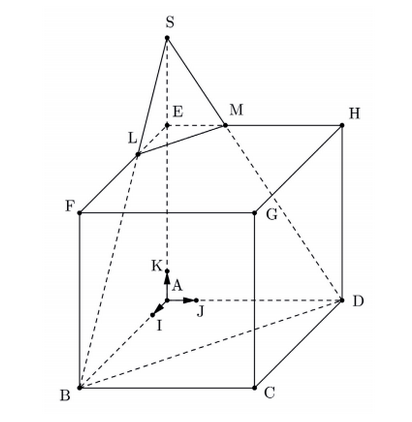
On munit l'espace du repère orthonormé $\left(A;\vec{AI},\vec{AJ},\vec{AK}\right)$ tel que: $I\in[AB]$, $J\in[AD]$, $K\in[AE]$ et $AI=AJ=AK=1$, l'unité graphique représentant 1 mètre. Les points $L$, $M$ et $S$ sont définis de la façon suivante:
- $L$ est le point tel que $\vec{FL}=\frac23\vec{FE}$;
- $M$ est le point d'intersection du plan $(BDL)$ et de la droite $(EH)$;
- $S$ est le point d'intersection des droites $(BL)$ et $(AK)$.
- Démontrer, sans calcul de coordonnées, que les droites $(LM)$ et $(BD)$ sont parallèles. Les plans $(FGH)$ et $(BCD)$ sont parallèles.
- Démontrer que les coordonnées du point $L$ sont $(2~;~0~;~6)$. Dans le repère $\left(A;\vec{AI},\vec{AJ},\vec{AK}\right)$ on a :
-
- Donner une représentation paramétrique de la droite $(BL)$. On a $B(6;0;0)$ et $\vec{BL}(-4;0;6)$
- Vérifier que les coordonnées du point $S$ sont $(0~;~0~;~9)$. Le point $S$ appartient à la droite $(AE)$. Ses coordonnées sont donc $\left(0;0;z_S\right)$.
Une représentation paramétrique de la droite $(BL)$ est :
$$\begin{cases} x=6-4t\\y=0\\z=6t\end{cases}, \quad t \in \mathbb R$$
$\quad$
De plus le point $S$ appartient à la droite $(BL)$.
On a donc :
$$\begin{align*} \begin{cases} 0=6-4t\\x_S=0\\y_S=0\\z_S=6t\end{cases} &\iff \begin{cases} t=\dfrac{3}{2}\\x_S=0\\y_S=0\\z_S=\dfrac{3}{2}\times 6\end{cases}
\end{align*}$$
Le point $S$ a donc pour coordonnées $(0;0;9)$.
$\quad$ - Soit $\vec{n}$ le vecteur de coordonnées $(3~;~3~;~2)$.
- Vérifier que $\vec{n}$ est normal au plan $(BDL)$. On a $B(6;0;0)$ et $D(0;6;0)$. Par conséquent $\vec{BD}(-6;6;0)$.
- Démontrer qu'une équation cartésienne du plan $(BDL)$ est: \[ 3x+3y+2z-18=0. \] Une équation cartésienne du plan $(BDL)$ est ainsi de la forme $$3x+3y+2z+d=0$$
- On admet que la droite $(EH)$ a pour représentation paramétrique: \[ \left\{ \begin{array}{rcl} x&=&0\\ y&=&s~~~~(s\in\mathbb R)\\ z&=&6 \end{array} \right. \] Calculer les coordonnées du point $M$. Le point $M$ est le point d’intersection de la droite $(EH)$ et du plan $(BDL)$.
De plus $\vec{BL}(-4;0;6)$.
Ainsi $\vec{n}.\vec{BD}=3\times (-6)+3\times 6+2\times 0=0$
et $\vec{n}.\vec{BL}=3\times (-4)+3\times 0+2\times 6=0$
Le vecteur $\vec{n}$ est orthogonal à deux vecteurs non colinéaires (ils n’ont pas la même coordonnée nulle) du plan $(BDL)$.
$\vec{n}$ est donc un vecteur normal au plan $(BDL)$.
$\quad$
Le point $B(6;0;0)$ appartient à ce plan.
Donc $3\times 6+0+0+d=0 \iff d=-18$.
Une équation cartésienne du plan $(BDL)$ est par conséquent $$3x+3y+2z-18=0$$
$\quad$
Ses coordonnées sont donc solution du système :
$\begin{align*} \begin{cases}x=0\\y=s\\z=6\\3x+3y+2z-18=0\end{cases} &\iff \begin{cases} x=0\\y=s\\z=6\\0+3s+12-18=0\end{cases} \\
&\iff \begin{cases} x=0\\y=s\\z=6\\3s=6 \end{cases} \\
&\iff \begin{cases} s=2\\x=0\\y=2\\z=6\end{cases}
\end{align*}$
Le point $M$ a pour coordonnées $(0;2;6)$.
$\quad$ - Calculer le volume du tétraèdre $SELM$. On rappelle que le volume $V$ d'un tétraèdre est donné par la formule suivante: \[ V=\frac13\times\text{Aire de la base}\times\text{Hauteur}. \] On a $\vec{EL}(2;0;0)$ donc $EL=2$
- L'artiste souhaite que la mesure de l'angle $\widehat{SLE}$ soit comprise entre 55$^{o}$ et 60$^{o}$.
Cette contrainte d'angle est-elle respectée ? On a $\vec{LS}(-2;0;3)$ et $\vec{LE}(-2;0;0)$.
La droite $(LM)$ est l’intersection du plan $(FGH)$ avec le plan $(SLM)$.
La droite $(BD)$ est l’intersection du plan $(BCD)$ avec le plan $(SLM)$.
Par conséquent les droites $(LM)$ et $(BD)$ sont parallèles.
$\quad$
$F(6;0;6)$, $E(0;0;6)$.
Par conséquent $\vec{FE}(-6;0;0)$.
Donc :
$$\begin{align*} \vec{FL}=\dfrac{2}{3}\vec{FE} &\iff \begin{cases} x_L-6=\dfrac{2}{3}\times (-6) \\y_L-0=\dfrac{2}{3}\times 0 \\z_L-6=\dfrac{2}{3}\times 0 \end{cases} \\
&\iff \begin{cases}x_L-6=-4\\y_L=0\\z_L=6\end{cases}
\end{align*}$$
Les coordonnées du point $L$ sont donc $(2;0;6)$.
$\quad$
et $\vec{EM}(0;2;0)$ donc $EM=2$
L’aire du triangle $ELM$ est donc $\mathscr{A}=\dfrac{2\times 2}{2}=2$ m$^2$.
De plus $\vec{ES}(0;0;3)$ donc $ES=3$.
Le volume du tétraèdre $SELM$ est $V=\dfrac{2\times 3}{3}=2$ m$^3$.
$\quad$
Par conséquent $LS=\sqrt{(-2)^2+0^2+3^2}=\sqrt{13}$ et $LE=2$
D’une part $\vec{LS}.\vec{LE}=-2\times (-2)+0+0=4$
D’autre part $\vec{LS}.\vec{LE}=2\sqrt{13}\cos\widehat{SLE}$
Donc $\cos\widehat{SLE}=\dfrac{4}{2\sqrt{13}}$
Ainsi $\widehat{SLE} \approx 56,3$°.
La contrainte d’angle est respectée.
$\quad$
- Vues: 42237
