Baccalauréat S Antilles Guyane19 juin 2018 - Correction Exercice 1
Correction de l'exercice 1 (5 points)
L'exploitant d'une forêt communale décide d'abattre des arbres afin de les vendre, soit aux habitants, soit à des entreprises. On admet que:
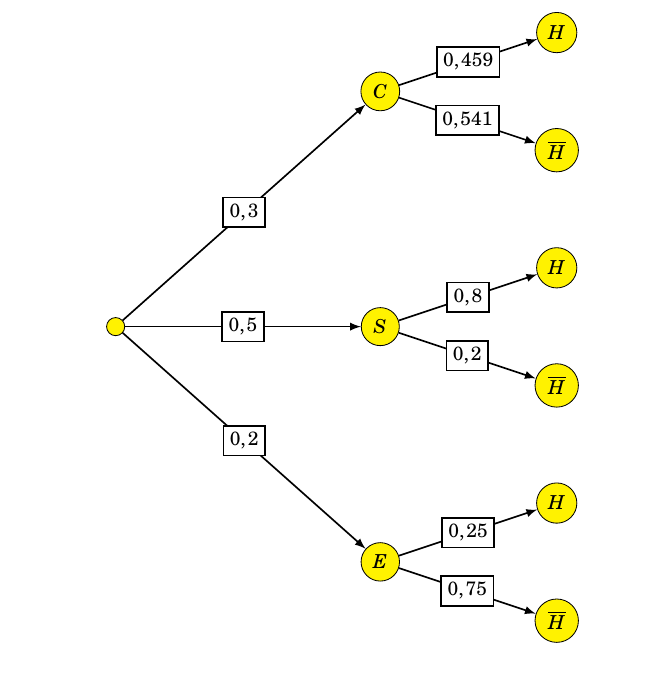
- parmi les arbres abattus, 30 % sont des chênes, 50 % sont des sapins et les autres sont des arbres d'essence secondaire (ce qui signifie qu'ils sont de moindre valeur);
- 45,9 % des chênes et 80 % des sapins abattus sont vendus aux habitants de la commune;
- les trois quarts des arbres d'essence secondaire abattus sont vendus à des entreprises.
Partie A
Parmi les arbres abattus, on en choisit un au hasard. On considère les événements suivants:
- $C$: « l'arbre abattu est un chêne»;
- $S$: « l'arbre abattu est un sapin»;
- $E$: « l'arbre abattu est un arbre d'essence secondaire»;
- $H$: « l'arbre abattu est vendu à un habitant de la commune».
- Construire un arbre pondéré complet traduisant la situation.
- Calculer la probabilité que l'arbre abattu soit un chêne vendu à un habitant de la commune. On veut calculer $p(C\cap H)=0,3\times 0,459=0,137~7$.
- Justifier que la probabilité que l'arbre abattu soit vendu à un habitant de la commune est égale à $0,587\;7$. D’après la formule des probabilités totales on a :
- Quelle est la probabilité qu'un arbre abattu vendu à un habitant de la commune soit un sapin ?
On donnera le résultat arrondi à $10^{-3}$. On veut calculer :
La probabilité que l’arbre abattu soit un chêne vendu à un habitant de la commune est $0,137~7$.
$\begin{align*} p(H)&=p(C\cap H)+p(S\cap H)+p(E\cap H) \\
&=0,3\times 0,459+0,5\times 0,8 +0,2\times 0,25 \\
&=0,137~7+0,4+0,05 \\
&=0,587~7
\end{align*}$
$\quad$
$\begin{align*} p_H(S)&=\dfrac{p(S\cap H)}{p(H)} \\
&=\dfrac{0,5\times 0,8}{0,587~7} \\
&\approx 0,681
\end{align*}$
La probabilité qu’un arbre abattu vendu à un habitant de la commune soit un sapin est environ égale à $0,681$.
$\quad$
Partie B
Le nombre d'arbres sur un hectare de cette forêt peut être modélisé par une variable aléatoire $X$ suivant une loi normale d'espérance $\mu= 4 \;000 $ et d'écart-type $\sigma=300$.
- Déterminer la probabilité qu'il y ait entre $3 ;400$ et $4\;600$ arbres sur un hectare donné de cette forêt. On donnera le résultat arrondi à $10^{-3}$. On a $p(3~400 \leqslant X \leqslant 4~600)=p(\mu-2\sigma \leqslant X\leqslant \mu+2\sigma) \approx 0,954$
- Calculer la probabilité qu'il y ait plus de $4\;500$ arbres sur un hectare donné de cette forêt. On donnera le résultat arrondi à $10^{-3}$. $p(X \geqslant 4~500)=0,5-p(4~000\leqslant X \leqslant 4~500) \approx 0,048$
ou
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
ou
2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$
Partie C
Sur une parcelle, on a compté 106 sapins dans un échantillon de 200 arbres.
Ce résultat remet-il en cause l'affirmation de l'exploitant ?
On a $n=200$ et $p=0,5$.
Donc $n \geqslant 30$, $np=100 \geqslant 5$ et $n(1-p)=100 \geqslant 5$.
Un intervalle de fluctuation asymptotique au seuil de $95\%$ est :
$\begin{align*} I_{200} &=\left[0,5-1,96\sqrt{\dfrac{0,5\times 0,5}{200}};0,5+1,96\sqrt{\dfrac{0,5\times 0,5}{200}}\right] \\
&\approx [0,431;0,570]
\end{align*}$
La fréquence observée est $f=\dfrac{106}{200}=0,53 \in I_{200}$.
Ce résultat ne remet pas en cause l’affirmation de l’exploitant.
$\quad$
- Vues: 42228
