Baccalauréat STI2D et STL spécialité SPCL Antilles-Guyane 19 juin 2018 - Exercice 2

Page 3 sur 8: Exercice 2

Exercice 2 7 points

Fonctions

On a représenté ci-dessous une des faces latérales d'une rampe de skate-board que l'on souhaite peindre.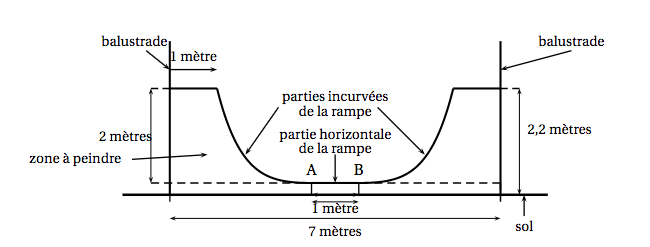

On sait de plus que la face latérale de cette rampe de skate-board admet comme axe de symétrie la médiatrice de [AB].

Partie A

On modélise la partie incurvée de la rampe située à gauche de l'axe de symétrie à l'aide de la fonction $f$ définie et dérivable sur l'intervalle $[0~;~2]$ par : \[f(x) = \left(0,5x^2 + ax + b\right)\text{e}^{-x}\] où $a$ et $b$ sont deux réels que l'on souhaite déterminer. On a tracé ci-après la courbe représentative $\mathcal{C}$ de $f$ dans un repère orthonormal d'unité 1 mètre.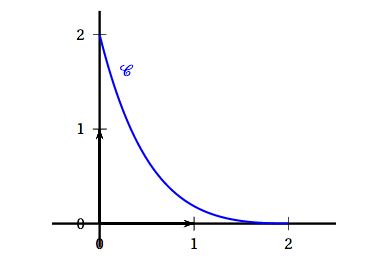

On sait que la courbe $\mathcal{C}$ passe par les points A$(2~;~0)$ et H$(0~;~2)$.

1. Déterminer $f(0)$ et $f(2)$.
2. Déduire de la question précédente le système d'équations vérifié par les réels $a$ et $b$.
3. Déterminer l'expression de $f(x)$.

 

Partie B

On considère maintenant que la fonction $f$ est définie et dérivable sur l'intervalle $[0~;~2] $ par : \[f(x) = \left(0,5x^2 - 2x + 2\right)\text{e}^{-x}.\]

1. Calculer $f'(x)$.
2. Montrer que la tangente à la courbe $\mathcal{C}$ au point A est l'axe des abscisses.
3. Justifier que le signe de $f'(x)$ est donné par le signe du trinôme $-0,5 x^2 + 3x - 4$.
4. En déduire le signe de $f'(x)$ puis le sens de variation de $f$ sur $[0~;~2]$.

 

Partie C

 

1. Justifier que la fonction $f$ est positive sur l'intervalle $[0~;~2]$.
2. On admet que la fonction $F$ définie par $F(x) = \left(- \frac{1}{2}x^2 + x - 1\right)\text{e}^{-x}$ sur l'intervalle $[0~;~2]$ est une primitive de la fonction $f$ sur $[0~;~2]$. Montrer que l'aire en m$^2$ de la partie délimitée par la courbe $\mathcal{C}$, l'axe des abscisses et les droites d'équation $x = 0$ et $x = 2$ est égale à $1 - \dfrac{1}{\text{e}^2}$.
3. En déduire l'aire de la zone à peindre. On donnera une valeur approchée du résultat à 0,01$~$m$^2$ près.