Suites, le cours
4. Comportement asymptotique d'une suite
4.1. Définition Suite convergente
On dit qu'une suite converge (ou admet une limite finie) lorsqu'il existe un réel $l$ tel que :
tout intervalle ouvert $I$ centré en $l$ contient tous les termes de la suite à partir d'un certain rang.
Lorsque $\left( u_n \right) $ converge vers $l$, on note alors : $l = \lim\limits_{n \to +\infty} u_n$.
Une suite non convergente est appelée suite divergente.
En formulant différemment cette définition, on obtient plusieurs variantes toutes équivalentes :
$\left( u_n \right) $ converge lorsqu'il existe un réel $l$ tel que :
1) Tout intervalle $ I = ]l - \epsilon, l + \epsilon[ (\epsilon \in \mathbb{R}_+^{\star})$ contient tous les termes de la suite à partir d'un certain rang.
2) Pour tout réel $\epsilon \in \mathbb{R}_+^{\star}$ , il existe un rang $N$ à partir duquel tous les $u_n$ vérifient $u_n \in ]l - \epsilon, l + \epsilon[$.
3) Pour tout réel $\epsilon \in \mathbb{R}_+^{\star}$, il existe un rang $N$ tel que pour tout indice $n$, on ait : $n\geq N \Rightarrow|u_n - l| < \epsilon$.
Graphiquement, cela se traduit ainsi :
Quelle que soit la largeur de la bande horizontale choisie, il existe un rang (ou un indice) à partir duquel tous les points de la représentation graphique de la suite sont situés dans cette bande.
Illustration avec la suite $\left( u_n \right) $ définie par :$u_n=\dfrac{3n+5(-1)^n}{2n}$:
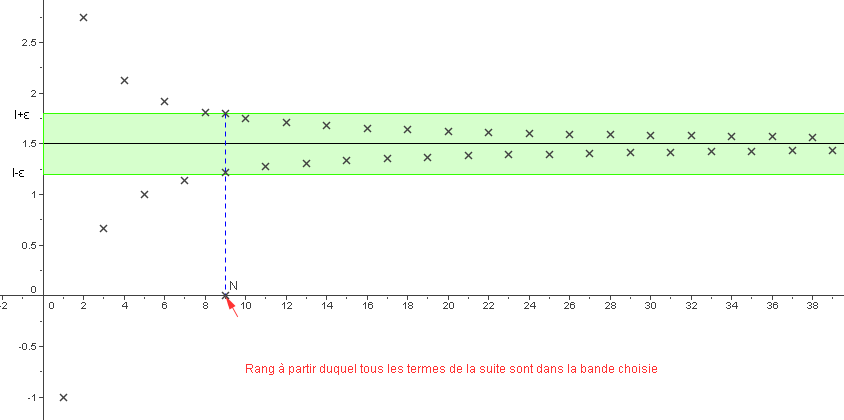
Sur cet exemple, le graphique permet de conjecturer que la suite $\left( u_n \right) $ converge vers $\dfrac{3}{2}$ , ce que le théorème des
gendarmes confirmera. (Voir 6.2.)
Remarque : on peut très bien travailler avec un intervalle $I$ qui est fermé (et donc avec des inégalités larges).
- Vues: 39881
