Probabilités conditionnelles : des exercices avec corrigé
Page 1 sur 3
Quelques exercices pour s'entraîner…
Exercice 1 ![]()
Enoncé 
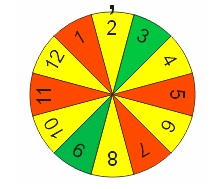 On fait tourner une roue comportant 12 secteurs de même taille numérotés de 1 à 12.
On fait tourner une roue comportant 12 secteurs de même taille numérotés de 1 à 12.
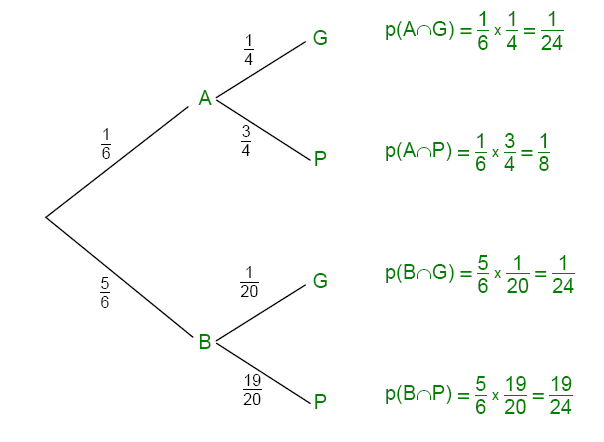
Les secteurs portant un numéro pair sont de couleur jaune, les secteurs portant un numéro multiple de trois et impair sont de couleur verte et les autres secteurs sont rouges. Si la roue s'arrête sur un secteur de couleur verte on tire un billet de loterie dans une urne A.
Dans les autres cas, on tire un billet de loterie dans une urne B.
Dans l'urne A un billet sur 4 est gagnant alors que dans l'urne B seulement un billet sur 20 est gagnant.
Calculer la probabilité d'obtenir un billet gagnant.

 On fait tourner une roue comportant 12 secteurs de même taille numérotés de 1 à 12.
On fait tourner une roue comportant 12 secteurs de même taille numérotés de 1 à 12. Les secteurs portant un numéro pair sont de couleur jaune, les secteurs portant un numéro multiple de trois et impair sont de couleur verte et les autres secteurs sont rouges. Si la roue s'arrête sur un secteur de couleur verte on tire un billet de loterie dans une urne A.
Dans les autres cas, on tire un billet de loterie dans une urne B.
Dans l'urne A un billet sur 4 est gagnant alors que dans l'urne B seulement un billet sur 20 est gagnant.
Calculer la probabilité d'obtenir un billet gagnant.
Indication 

Corrigé 

Exercice 2 
Enoncé  On considère le jeu suivant: On jette une première fois une pièce de monnaie ;
On considère le jeu suivant: On jette une première fois une pièce de monnaie ;
si on obtient face, on gagne 4 euros et le jeu s'arrête ;
si on obtient pile, on gagne 1 euro et le jeu se poursuit ;
on jette alors une deuxième fois la pièce ;
si on obtient face on gagne 2 euros et le jeu s'arrête ;
si on obtient pile on gagne 1 euro et le jeu se poursuit ;
on jette alors une troisième et dernière fois la pièce ;
si on obtient face, on gagne 2 euros ; si on obtient pile, on gagne 1 euro.
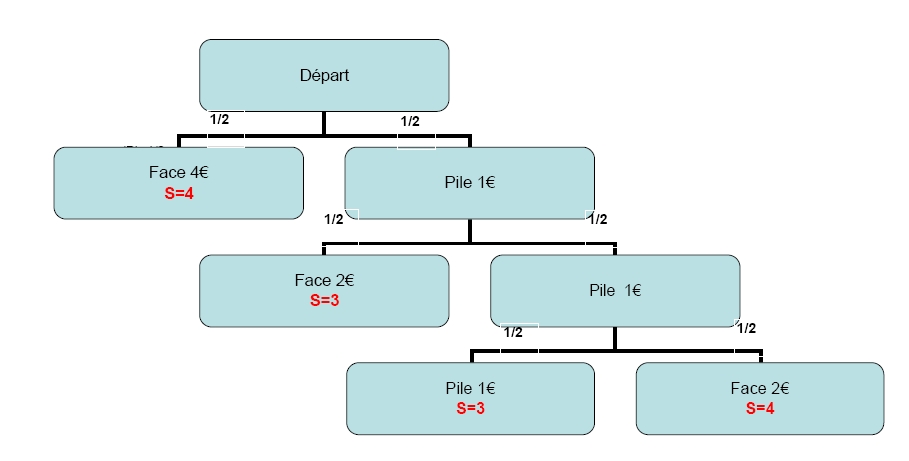
Représenter le jeu par un arbre pondéré. Quelle est la probabilité d'avoir obtenu 4 euros à la fin du jeu ?
 On considère le jeu suivant: On jette une première fois une pièce de monnaie ;
On considère le jeu suivant: On jette une première fois une pièce de monnaie ; si on obtient face, on gagne 4 euros et le jeu s'arrête ;
si on obtient pile, on gagne 1 euro et le jeu se poursuit ;
on jette alors une deuxième fois la pièce ;
si on obtient face on gagne 2 euros et le jeu s'arrête ;
si on obtient pile on gagne 1 euro et le jeu se poursuit ;
on jette alors une troisième et dernière fois la pièce ;
si on obtient face, on gagne 2 euros ; si on obtient pile, on gagne 1 euro.
Représenter le jeu par un arbre pondéré. Quelle est la probabilité d'avoir obtenu 4 euros à la fin du jeu ?
Corrigé
Exercice 3 ![]()
Enoncé  On soumet, à la naissance, une population d'enfants à un test pour dépister la présence d'un caractère génétique A.
On soumet, à la naissance, une population d'enfants à un test pour dépister la présence d'un caractère génétique A.
La probabilité qu'un enfant ayant le caractère $A$ ait un test positif est 0,99.
La probabilité qu'un enfant n'ayant pas le caractère $A$ ait un test négatif est 0,98.
 On soumet, à la naissance, une population d'enfants à un test pour dépister la présence d'un caractère génétique A.
On soumet, à la naissance, une population d'enfants à un test pour dépister la présence d'un caractère génétique A. La probabilité qu'un enfant ayant le caractère $A$ ait un test positif est 0,99.
La probabilité qu'un enfant n'ayant pas le caractère $A$ ait un test négatif est 0,98.
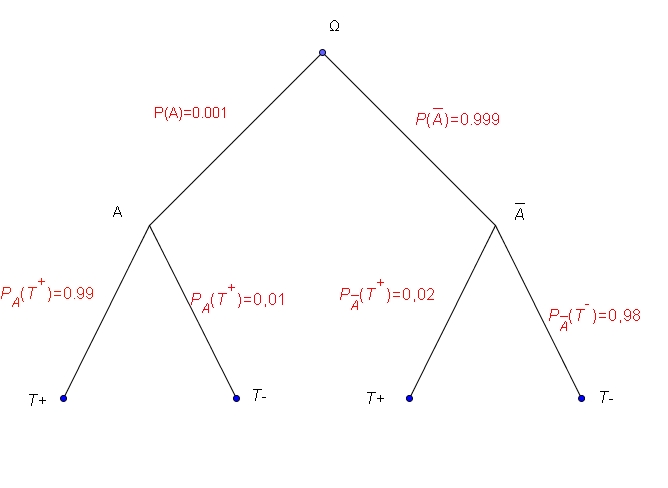
- On utilise le test avec une population pour laquelle des études statistiques ont montré qu'un enfant sur 1000 était porteur du caractère A.
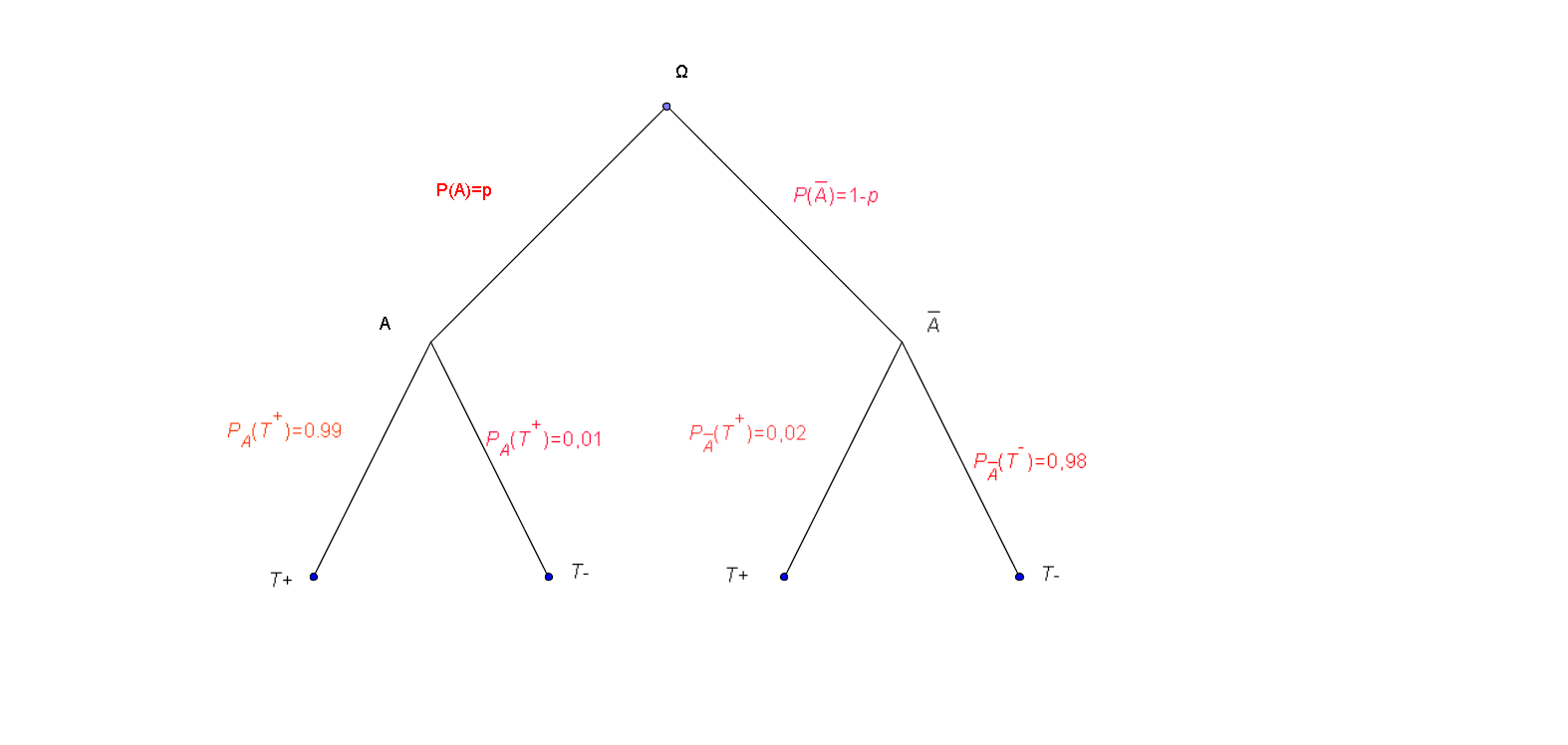
Représenter la situation par un arbre pondéré.
Déterminer la probabilité qu'un enfant pris au hasard dans la population étudiée ait un test positif.
Déterminer la probabilité qu'un enfant ayant un test positif soit porteur du caractère $A$.
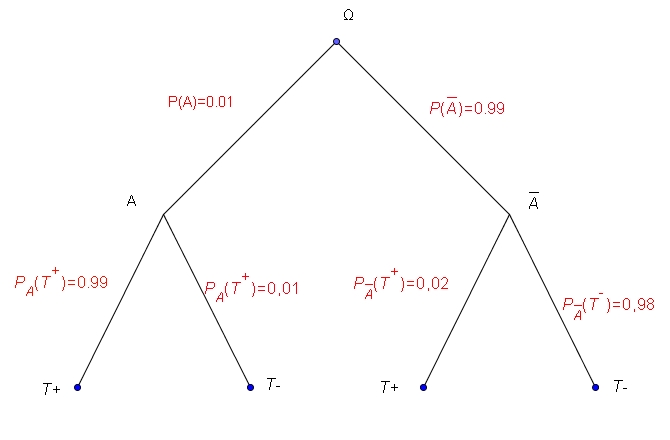
Donner une valeur approchée de ce résultat en pourcentage avec une décimale. - On utilise le test avec une population pour laquelle des études statistiques ont montré qu'un enfant sur 100 était porteur du caractère $A$.
Déterminer la probabilité qu'un enfant ayant un test positif soit porteur du caractère $A$.
Donner ce résultat en pourcentage avec une décimale. - On utilise le test avec une population pour laquelle des études statistiques ont montré qu'un enfant avait une probabilité $p$ d'être porteur du caractère $A$.
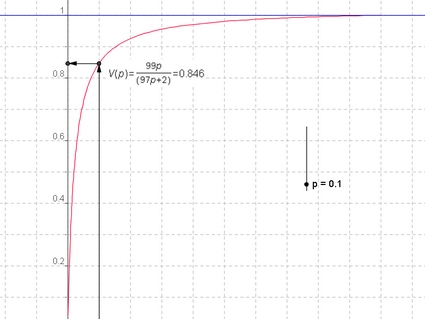
Déterminer, en fonction de $p$, la probabilité $V(p)$ qu'un enfant ayant un test positif soit porteur du caractère $A$.
$V(p)$ est la valeur prédictive du test. Représenter $V(p)$ en fonction de $p$ et commenter.
Exercice 4 
Enoncé 

- On tire une carte dans un jeu de 32 cartes. On considère l'événement $C$ : " tirer un coeur " et l'événement $A $: " tirer un as ". Les événements $A$ et $C$ sont-ils indépendants ?
- On tire simultanément deux cartes dans un jeu de 32 cartes.
- On considère l'événement $C'$ : " tirer deux coeurs " et l'événement $A'$ : " tirer deux as ". Les événements $A'$ et $C'$ sont-ils indépendants ?
- On considère $C'' $: " tirer un coeur et un seul " et $A''$ : " tirer un as et un seul ". Les événements $A''$ et $C''$ sont-ils indépendants ?
Exercice 5 
Enoncé  On jette simultanément un dé bleu et un dé rouge. Le dé bleu a des faces numérotées 1 ; 1 ; 2 ; 2 ; 5 ; 6 Le dé rouge a des faces numérotées : 1 ; 2 ; 3 ; 4 ; 5 ; 6. On appelle $S$ la variable aléatoire qui à un lancer fait correspondre la somme des deux numéros tirés.
On jette simultanément un dé bleu et un dé rouge. Le dé bleu a des faces numérotées 1 ; 1 ; 2 ; 2 ; 5 ; 6 Le dé rouge a des faces numérotées : 1 ; 2 ; 3 ; 4 ; 5 ; 6. On appelle $S$ la variable aléatoire qui à un lancer fait correspondre la somme des deux numéros tirés.
 On jette simultanément un dé bleu et un dé rouge. Le dé bleu a des faces numérotées 1 ; 1 ; 2 ; 2 ; 5 ; 6 Le dé rouge a des faces numérotées : 1 ; 2 ; 3 ; 4 ; 5 ; 6. On appelle $S$ la variable aléatoire qui à un lancer fait correspondre la somme des deux numéros tirés.
On jette simultanément un dé bleu et un dé rouge. Le dé bleu a des faces numérotées 1 ; 1 ; 2 ; 2 ; 5 ; 6 Le dé rouge a des faces numérotées : 1 ; 2 ; 3 ; 4 ; 5 ; 6. On appelle $S$ la variable aléatoire qui à un lancer fait correspondre la somme des deux numéros tirés.
- Donner la loi de probabilité de S.
- Sachant que la somme $S$ est égale à 7, quelle est la probabilité que le dé bleu ait donné le numéro 2 ?
- Sachant que la somme $S$ est égale à 7, quelle est la probabilité que le dé rouge ait donné le numéro 2?
- Sachant que la somme $S$ est égale à 7, quelle est la probabilité que l'un des dés ait donné le numéro 2 ?
- Démontrer que les événements $S = 7$ et " le dé bleu a donné le numéro 2 " sont indépendants.
Page
- Vues: 32253