Probabilités conditionnelles : des exercices avec corrigé série 2
Quelques exercices pour s'entraîner…
I
Exercice 6 ![]()
Enoncé  On considère un dé cubique dont les faces sont numérotées de 1 à 6. On jette successivement deux fois le dé et on note les numéros obtenus.
On considère un dé cubique dont les faces sont numérotées de 1 à 6. On jette successivement deux fois le dé et on note les numéros obtenus.
On appelle $X$ la variable aléatoire égale au premier numéro obtenu.
On appelle $Y$ la variable aléatoire qui prend la valeur 0 si " la somme des deux numéros est un nombre premier " et qui prend la valeur 1 sinon.
On appelle $Z$ la variable aléatoire qui prend la valeur 0 si " la somme des deux numéros augmentée de 4 est un nombre premier " et qui prend la valeur 1 sinon.
Les variables aléatoires $X$ et $Y$ sont-elles indépendantes ?
Les variables aléatoires $X$ et $Z$ sont-elles indépendantes ?
 On considère un dé cubique dont les faces sont numérotées de 1 à 6. On jette successivement deux fois le dé et on note les numéros obtenus.
On considère un dé cubique dont les faces sont numérotées de 1 à 6. On jette successivement deux fois le dé et on note les numéros obtenus. On appelle $X$ la variable aléatoire égale au premier numéro obtenu.
On appelle $Y$ la variable aléatoire qui prend la valeur 0 si " la somme des deux numéros est un nombre premier " et qui prend la valeur 1 sinon.
On appelle $Z$ la variable aléatoire qui prend la valeur 0 si " la somme des deux numéros augmentée de 4 est un nombre premier " et qui prend la valeur 1 sinon.
Les variables aléatoires $X$ et $Y$ sont-elles indépendantes ?
Les variables aléatoires $X$ et $Z$ sont-elles indépendantes ?
Exercice 7 
Enoncé  On tire au hasard deux cartes dans un jeu de 32 cartes. On appelle $X$ la variable aléatoire égale au nombre de coeurs obtenus et $Y$ la variable aléatoire qui prend la valeur 1 si les deux cartes tirées sont consécutives : "As et roi" ou "roi et dame" ou ... ou "8 et 7" et qui prend la valeur 0 si les deux cartes ne sont pas consécutives.
On tire au hasard deux cartes dans un jeu de 32 cartes. On appelle $X$ la variable aléatoire égale au nombre de coeurs obtenus et $Y$ la variable aléatoire qui prend la valeur 1 si les deux cartes tirées sont consécutives : "As et roi" ou "roi et dame" ou ... ou "8 et 7" et qui prend la valeur 0 si les deux cartes ne sont pas consécutives.
Les variables aléatoires $X$ et $Y$ sont elles indépendantes ?
 On tire au hasard deux cartes dans un jeu de 32 cartes. On appelle $X$ la variable aléatoire égale au nombre de coeurs obtenus et $Y$ la variable aléatoire qui prend la valeur 1 si les deux cartes tirées sont consécutives : "As et roi" ou "roi et dame" ou ... ou "8 et 7" et qui prend la valeur 0 si les deux cartes ne sont pas consécutives.
On tire au hasard deux cartes dans un jeu de 32 cartes. On appelle $X$ la variable aléatoire égale au nombre de coeurs obtenus et $Y$ la variable aléatoire qui prend la valeur 1 si les deux cartes tirées sont consécutives : "As et roi" ou "roi et dame" ou ... ou "8 et 7" et qui prend la valeur 0 si les deux cartes ne sont pas consécutives. Les variables aléatoires $X$ et $Y$ sont elles indépendantes ?
Exercice 8 
Enoncé  Une étude a porté sur les véhicules d'un parc automobile. On a constaté que: " lorsqu'on choisit au hasard un véhicule du parc automobile la probabilité qu'il présente un défaut de freinage est de 0,67 ; " lorsqu'on choisit au hasard dans ce parc un véhicule présentant un défaut de freinage, la probabilité qu'il présente aussi un défaut d'éclairage est de 0,48 ; " lorsqu'on choisit au hasard dans ce parc un véhicule ne présentant pas de défaut de freinage, la probabilité qu'il ne présente pas non plus de défaut d'éclairage est de 0,75.
Une étude a porté sur les véhicules d'un parc automobile. On a constaté que: " lorsqu'on choisit au hasard un véhicule du parc automobile la probabilité qu'il présente un défaut de freinage est de 0,67 ; " lorsqu'on choisit au hasard dans ce parc un véhicule présentant un défaut de freinage, la probabilité qu'il présente aussi un défaut d'éclairage est de 0,48 ; " lorsqu'on choisit au hasard dans ce parc un véhicule ne présentant pas de défaut de freinage, la probabilité qu'il ne présente pas non plus de défaut d'éclairage est de 0,75.
 Une étude a porté sur les véhicules d'un parc automobile. On a constaté que: " lorsqu'on choisit au hasard un véhicule du parc automobile la probabilité qu'il présente un défaut de freinage est de 0,67 ; " lorsqu'on choisit au hasard dans ce parc un véhicule présentant un défaut de freinage, la probabilité qu'il présente aussi un défaut d'éclairage est de 0,48 ; " lorsqu'on choisit au hasard dans ce parc un véhicule ne présentant pas de défaut de freinage, la probabilité qu'il ne présente pas non plus de défaut d'éclairage est de 0,75.
Une étude a porté sur les véhicules d'un parc automobile. On a constaté que: " lorsqu'on choisit au hasard un véhicule du parc automobile la probabilité qu'il présente un défaut de freinage est de 0,67 ; " lorsqu'on choisit au hasard dans ce parc un véhicule présentant un défaut de freinage, la probabilité qu'il présente aussi un défaut d'éclairage est de 0,48 ; " lorsqu'on choisit au hasard dans ce parc un véhicule ne présentant pas de défaut de freinage, la probabilité qu'il ne présente pas non plus de défaut d'éclairage est de 0,75.
- Déterminer la probabilité pour qu'un véhicule choisi au hasard présente un défaut d'éclairage. Traduire le résultat en terme de pourcentages.
- Déterminer la probabilité pour qu'un véhicule choisi au hasard parmi les véhicules présentant un défaut d'éclairage présente aussi un défaut de freinage. Traduire le résultat en terme de pourcentages.
Exercice 9 
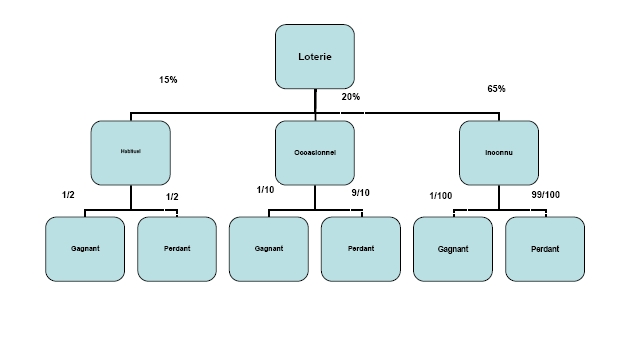
Enoncé  Lors d'une journée "portes ouvertes" dans un commerce, on remet à chaque visiteur un ticket numéroté qui permet de participer à une loterie.
Lors d'une journée "portes ouvertes" dans un commerce, on remet à chaque visiteur un ticket numéroté qui permet de participer à une loterie.
Lorsqu'un visiteur arrive 3 cas peuvent se présenter :
" le visiteur est reconnu comme client habituel et on lui remet un ticket dont le numéro se termine par 0 ;
" le visiteur est reconnu comme client occasionnel et on lui remet un ticket dont le numéro se termine par 1 ;
le visiteur n'est pas reconnu et on lui remet un ticket dont le numéro se termine par 5 ;
La probabilité qu'un ticket dont le numéro se termine par 0 gagne un cadeau est de 0,5 ;
La probabilité qu'un ticket dont le numéro se termine par 1 gagne un cadeau est de 0,1 ;
La probabilité qu'un ticket dont le numéro se termine par 5 gagne un cadeau est de 0,01.
Parmi les visiteurs 15\% sont reconnus comme clients habituels et 20\% comme clients occasionnels.
 Lors d'une journée "portes ouvertes" dans un commerce, on remet à chaque visiteur un ticket numéroté qui permet de participer à une loterie.
Lors d'une journée "portes ouvertes" dans un commerce, on remet à chaque visiteur un ticket numéroté qui permet de participer à une loterie. Lorsqu'un visiteur arrive 3 cas peuvent se présenter :
" le visiteur est reconnu comme client habituel et on lui remet un ticket dont le numéro se termine par 0 ;
" le visiteur est reconnu comme client occasionnel et on lui remet un ticket dont le numéro se termine par 1 ;
le visiteur n'est pas reconnu et on lui remet un ticket dont le numéro se termine par 5 ;
La probabilité qu'un ticket dont le numéro se termine par 0 gagne un cadeau est de 0,5 ;
La probabilité qu'un ticket dont le numéro se termine par 1 gagne un cadeau est de 0,1 ;
La probabilité qu'un ticket dont le numéro se termine par 5 gagne un cadeau est de 0,01.
Parmi les visiteurs 15\% sont reconnus comme clients habituels et 20\% comme clients occasionnels.
- On choisit un visiteur au hasard.
Quelle est la probabilité pour qu'il gagne un cadeau ? - Un visiteur a gagné un cadeau. Quelle est la probabilité qu'il ait été reconnu comme client habituel ?
Exercice 10 
Enoncé  Variables aléatoires et arbres Un industriel fabrique des tablettes de chocolat. Pour promouvoir la vente de ces tablettes, il décide d'offrir des places de cinéma dans la moitié des tablettes mises en vente. Parmi les tablettes gagnantes, 60\% permettent de gagner exactement une place de cinéma et 40\% exactement deux places de cinéma. On note PB(A) la probabilité conditionnelle de l'événement A sachant que l'événement B est réalisé.
Variables aléatoires et arbres Un industriel fabrique des tablettes de chocolat. Pour promouvoir la vente de ces tablettes, il décide d'offrir des places de cinéma dans la moitié des tablettes mises en vente. Parmi les tablettes gagnantes, 60\% permettent de gagner exactement une place de cinéma et 40\% exactement deux places de cinéma. On note PB(A) la probabilité conditionnelle de l'événement A sachant que l'événement B est réalisé.
 Variables aléatoires et arbres Un industriel fabrique des tablettes de chocolat. Pour promouvoir la vente de ces tablettes, il décide d'offrir des places de cinéma dans la moitié des tablettes mises en vente. Parmi les tablettes gagnantes, 60\% permettent de gagner exactement une place de cinéma et 40\% exactement deux places de cinéma. On note PB(A) la probabilité conditionnelle de l'événement A sachant que l'événement B est réalisé.
Variables aléatoires et arbres Un industriel fabrique des tablettes de chocolat. Pour promouvoir la vente de ces tablettes, il décide d'offrir des places de cinéma dans la moitié des tablettes mises en vente. Parmi les tablettes gagnantes, 60\% permettent de gagner exactement une place de cinéma et 40\% exactement deux places de cinéma. On note PB(A) la probabilité conditionnelle de l'événement A sachant que l'événement B est réalisé.
- Un client achète une tablette de chocolat. On considère les événements suivants: $G$ = "le client achète une tablette gagnante" U = "le client gagne exactement une place de cinéma" $D $= "le client gagne exactement deux places de cinéma"
- Donner $P(G)$, $P_{G}(U)$ et $P_{G}(D)$
- Montrer que la probabilité de gagner exactement une place de cinéma est égale à 0,3.
- Soit $X$ la variable aléatoire égale au nombre de places de cinéma gagnées par le client. Déterminer la loi de probabilité de $X$. Calculer l'espérance mathématique de $X$.
- Un autre client achète deux jours de suite une tablette de chocolat.
- Déterminer la probabilité qu'il ne gagne aucune place de cinéma.
- Déterminer la probabilité qu'il gagne au moins une place de cinéma.
- Montrer que la probabilité qu'il gagne exactement deux places de cinéma est égale à 0,29.
Exercice 12 
Enoncé  Problème de déconditionnement
Problème de déconditionnement
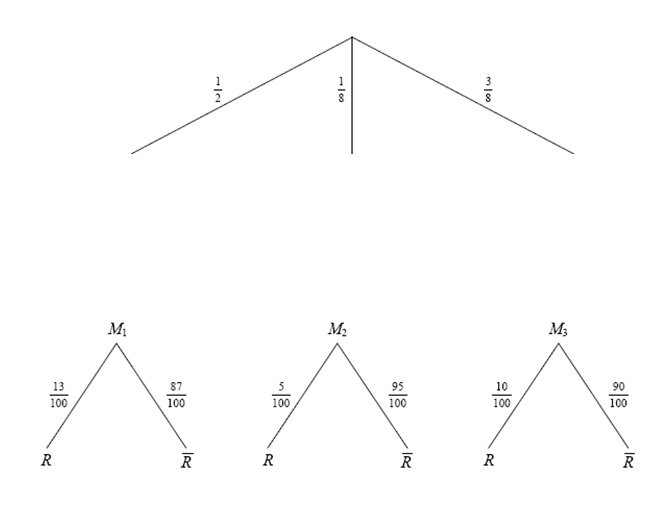
Un grossiste en appareils ménagers est approvisionné par trois marques, notées respectivement $M_1, M_2$ et $M_3$. La moitié des appareils de son stock provient de $M_1$, un huitième de $M_2$, et trois huitièmes de $M_3$. Ce grossiste sait que dans son stock, 13\% des appareils de la marque $M_1$ sont rouges, que 5\% des appareils de la marque $M_2$ sont rouges et que 10\% des appareils de la marque $M_3$ le sont aussi. On donnera les résultats sous forme de fractions. On choisit au hasard un appareil emballé dans le stock de ce grossiste :
 Problème de déconditionnement
Problème de déconditionnement Un grossiste en appareils ménagers est approvisionné par trois marques, notées respectivement $M_1, M_2$ et $M_3$. La moitié des appareils de son stock provient de $M_1$, un huitième de $M_2$, et trois huitièmes de $M_3$. Ce grossiste sait que dans son stock, 13\% des appareils de la marque $M_1$ sont rouges, que 5\% des appareils de la marque $M_2$ sont rouges et que 10\% des appareils de la marque $M_3$ le sont aussi. On donnera les résultats sous forme de fractions. On choisit au hasard un appareil emballé dans le stock de ce grossiste :
- Quelle est la probabilité qu'il vienne de $M_3$ ?
- Quelle est la probabilité qu'il soit rouge sachant qu'il vienne de $M_2$ ?
- Quelle est la probabilité que l'appareil choisi ne soit pas de couleur rouge ?
- Après examen, on s'aperçoit que l'appareil choisi est rouge. Quelle est la probabilité qu'il soit de la marque $M_1$ ?
Exercice 13 
Enoncé  Probabilités conditionnelles et suite arithmético-géométrique:
Probabilités conditionnelles et suite arithmético-géométrique:
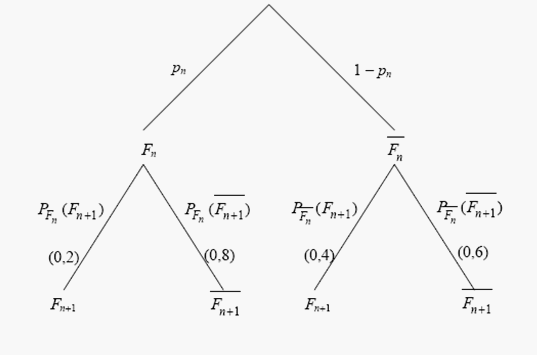
Un fumeur essaye de réduire sa consommation. On admet qu'il fonctionne toujours suivant les conditions :
 Probabilités conditionnelles et suite arithmético-géométrique:
Probabilités conditionnelles et suite arithmético-géométrique: Un fumeur essaye de réduire sa consommation. On admet qu'il fonctionne toujours suivant les conditions :
- $C_1$ : S'il reste un jour sans fumer, alors il fume le lendemain avec une probabilité de 0,4.
- $C_2$ : Par contre, s'il cède et fume un jour, alors la probabilité qu'il fume le lendemain est de 0,2.
- Calculer $p_{n+1}$. On montrera que $p_{n+1}= -0.2p_{n}+0.4$
- On considère la suite $(u_{n})$ définie par $u_{n}= p_{n}-\dfrac{1}{3}$ .
- Montrer que est géométrique.
- En déduire $p_{n}$ en fonction de $n$.
- Déterminer la limite de $p_{n}$. Conclusion ?
- Vues: 10588