Lois à densité , exercices
Exercice 1 ![]()

Métropole Septembre 2014
Dans cet exercice, on s’intéresse au mode de fonctionnement de deux restaurants : sans réservation ou avec réservation préalable.
- Le premier restaurant fonctionne sans réservation mais le temps d’attente pour obtenir une table est souvent un problème pour les clients.
$\quad$
On modélise ce temps d’attente en minutes par une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda$ où $\lambda$ est un réel strictement positif. On rappelle que l’espérance mathématique de $X$ est égale à $\dfrac{1}{\lambda}$.
$\quad$
Une étude statistique a permis d’observer que le temps moyen d’attente pour obtenir une table est de $10$ minutes.
a. Déterminer la valeur de $\lambda$.
$\quad$
b. Quelle est la probabilité qu’un client attende entre $10$ et $20$ minutes pour obtenir une table ? On arrondira à $10^{-4}$.
$\quad$
c. Un client attend depuis $10$ minutes. Quelle est la probabilité qu’il doive attendre au moins $5$ minutes de plus pour obtenir une table ? On arrondira à $10^{-4}$.
$\quad$ - Le deuxième restaurant a une capacité d’accueil de $70$ places et ne sert que des personnes ayant réservé au préalable. La probabilité qu’une personne ayant réservé se présente au restaurant est estimée à $0,8$.
$\quad$
On note $n$ le nombre de réservations prises par le restaurant et $Y$ la variable aléatoire correspondant au nombre de personnes ayant réservé qui se présentent au restaurant.
$\quad$
On admet que les comportements des personnes ayant réservé sont indépendants les uns des autres. La variable aléatoire $Y$ suit alors une loi binomiale.
a. Préciser, en fonction de $n$, les paramètres de la loi de la variable aléatoire $Y$, son espérance mathématique $E(Y)$ et son écart-type $\sigma(Y)$.
$\quad$
b. Dans cette question, on désigne par $Z$ une variable aléatoire suivant la loi normale $\mathscr{N}\left(\mu, \sigma^2\right)$ de moyenne $\mu = 64,8$ et d’écart-type $\sigma = 3,6$.
$\quad$
Calculer la probabilité $p_{1}$ de l’évènement $\{Z \leqslant 71\}$ à l’aide de la calculatrice.
$\quad$
c. On admet que lorsque $n = 81$, $p_{1}$ est une valeur approchée à $10^{-2}$ près de la probabilité $p(Y \leqslant 70)$ de l’évènement $\{Y \leqslant 70\}$.
$\quad$
Le restaurant a reçu $81$ réservations.
Quelle est la probabilité qu’il ne puisse pas accueillir certains des clients qui ont réservé et se présentent ?
$\quad$

d’après Amérique du Nord mai 2013
Les parties A et B peuvent être traitées indépendamment les unes des autres
Une boulangerie industrielle utilise une machine pour fabriquer des pains de campagne pesant en moyenne $400$ grammes. Pour être vendus aux clients, ces pains doivent peser au moins $385$ grammes. Un pain dont la masse est strictement inférieure à $385$ grammes est un pain non-commercialisable, un pain dont la masse est supérieure ou égale à $385$ grammes est commercialisable.
La masse d’un pain fabriqué par la machine peut être modélisée par une variable aléatoire $X$ suivant la loi normale d’espérance $\mu = 400$ et d’écart-type $\sigma = 11$.
Les probabilités seront arrondies au millième le plus proche
Partie A
On pourra utiliser le tableau suivant dans lequel les valeurs sont arrondies au millième le plus proche.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
x&380&385&390&395&400&405&410&415&420\\ \hline
P(X \leqslant x)&0,035&0,086&0,182&0,325&0,5&0,675&0,818&0,914&0,965\\ \hline
\end{array}$$
- Calculer $P(390 \leqslant X \leqslant 410)$.
$\quad$ - Calculer la probabilité $p$ qu’un pain choisi au hasard dans la production soit commercialisable.
$\quad$ - Le fabricant trouve cette probabilité $p$ trop faible. Il décide de modifier ses méthodes de production afin de faire varier la valeur de $\sigma$ sans modifier celle de $\mu$.
Pour quelle valeur de $\sigma$ la probabilité qu’un pain soit commercialisable est-elle égale à $96\%$ ? On arrondira le résultat au dixième.
On pourra utiliser le résultat suivant : lorsque $Z$ est une variable aléatoire qui suit la loi normale d’espérance $0$ et d’écart-type $1$, on a $P(Z \leqslant -1,751) \approx 0,040$.
$\quad$
Partie B
Le boulanger utilise une balance électronique. Le temps de fonctionnement sans dérèglement, en jours, de cette balance électronique est une variable aléatoire $T$ qui suit une loi exponentielle de paramètre $\lambda$.
- On sait que la probabilité que la balance électronique ne se dérègle pas avant $30$ jours est de $0,913$. En déduire la valeur de $\lambda$ arrondie au millième.
$\quad$
Dans toute la suite on prendra $\lambda = 0,003$.
$\quad$ - Quelle est la probabilité que la balance électronique fonctionne encore sans dérèglement après $90$ jours, sachant qu’elle a fonctionné sans dérèglement $60$ jours ?
$\quad$ - Le vendeur de cette balance électronique a assuré au boulanger qu’il y avait une chance sur deux pour que la balance ne se dérègle pas avant un an. A-t-il raison ? Si non, pour combien de jours est-ce vrai ?
$\quad$

Liban mai 2013
L’entreprise Fructidoux fabrique des compotes qu’elle conditionne en petits pots de $50$ grammes. Elle souhaite leur attribuer la dénomination « compote allégée ».
La législation impose alors que la teneur en sucre, c’est-à-dire la proportion de sucre dans la compote, soit comprise entre $0,16$ et $0,18$. On dit dans ce cas que le petit pot de compote est conforme.
L’entreprise possède deux chaînes de fabrication $F_{1}$ et $F_{2}$.
Les parties A et B peuvent être traitées indépendamment
Partie A
La chaîne de production $F_{2}$ semble plus fiable que la chaîne de production $F_{1}$. Elle est cependant moins rapide.
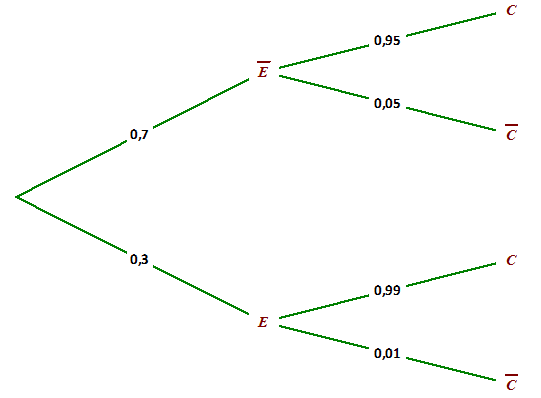
Ainsi, dans la production totale, $70\%$ des petits pots proviennent de la chaîne $F_{1}$ et $30\%$ de la chaîne $F_{2}$.
La chaîne $F_{1}$ produit $5\%$ de compotes non conformes et la chaîne $F_{2}$ en produit $1\%$.
On prélève au hasard un petit pot dans la production totale. On considère les événements :
$E$ : « Le petit pot provient de la chaîne $F_{2}$ »
$C$ : « Le petit pot est conforme. »
$\quad$
- Construire un arbre pondéré sur lequel on indiquera les données qui précèdent.
$\quad$ - Calculer la probabilité de l’événement : « Le petit pot est conforme et provient de la chaîne de production $F_{1}$. »
$\quad$ - Déterminer la probabilité de l’événement $C$.
$\quad$ - Déterminer, à $10^{-3}$ près, la probabilité de l’événement $E$ sachant que l’événement $C$ est réalisé.
$\quad$
Partie B
- On note $X$ la variable aléatoire qui, à un petit pot pris au hasard dans la production de la chaîne $F_{1}$, associe sa teneur en sucre.
On suppose que $X$ suit la loi normale d’espérance $m_{1} = 0,17$ et d’écart-type $\sigma_{1} = 0,006$.
Dans la suite, on pourra utiliser le tableau ci-dessous.
$$\begin{array}{|c|c|c|}\hline
\alpha& \beta&P(\alpha \leqslant X \leqslant \beta)\\ \hline
0,13 &0,15 &0,000~4\\ \hline
0,14 &0,16 &0,047~8\\ \hline
0,15 &0,17 &0,499~6 \\ \hline
0,16 &0,18 &0,904~4\\ \hline
0,17 &0,19 &0,499~6\\ \hline
0,18 &0,20 &0,047~8\\ \hline
0,19 &0,21 &0,000~4 \\ \hline
\end{array}$$
Donner une valeur approchée à $10^{-4}$ près de la probabilité qu’un petit pot prélevé au hasard dans la production de la chaîne $F_{1}$ soit conforme.
$\quad$ - On note $Y$ la variable aléatoire qui, à un petit pot pris au hasard dans la production de la chaîne $F_{2}$, associe sa teneur en sucre.
On suppose que $Y$ suit la loi normale d’espérance $m_{2} = 0,17$ et d’écart-type $\sigma_{2}$.
On suppose de plus que la probabilité qu’un petit pot prélevé au hasard dans la production de la chaîne $F_{2}$ soit conforme est égale à $0,99$.
Soit Z la variable aléatoire définie par $Z = \dfrac{Y – m_{2}}{\sigma_{2}}$.
a. Quelle loi la variable aléatoire $Z$ suit-elle ?
$\quad$
b. Déterminer, en fonction de $\sigma_{2}$ l’intervalle auquel appartient $Z$ lorsque $Y$ appartient à l’intervalle $[0,16~;~0,18]$.
$\quad$
c. En déduire une valeur approchée à $10^{-3}$ près de $\sigma_{2}$.
On pourra utiliser le tableau donné ci-dessous, dans lequel la variable aléatoire $Z$ suit la loi normale d’espérance $0$ et d’écart-type $1$.
$$\begin{array}{|c|c|}\hline
\beta&P(- \beta \leqslant Z \leqslant \beta)\\ \hline
2,432~4 &0,985\\ \hline
2,457~3 &0,986\\ \hline
2,483~8 &0,987\\ \hline
2,512~1 &0,988\\ \hline
2,542~7 &0,989\\ \hline
2,575~8 &0,990\\ \hline
2,612~1 &0,991\\ \hline
2,652~1 &0,992\\ \hline
2,696~8 &0,993\\ \hline
\end{array}$$
$\quad$

d’après Amérique du Nord mai 2014
Dans cet exercice, tous les résultats demandés seront arrondis à $10^{-3}$ près.
Une grande enseigne de cosmétiques lance une nouvelle crème hydratante.
Conditionnement des pots
Cette enseigne souhaite vendre la nouvelle crème sous un conditionnement de $50$ mL et dispose pour ceci de pots de contenance maximale $55$ mL.
On dit qu’un pot de crème est non conforme s’il contient moins de $49$ mL de crème.
- Plusieurs séries de tests conduisent à modéliser la quantité de crème, exprimée en mL, contenue dans chaque pot par une variable aléatoire $X$ qui suit la loi normale d’espérance $\mu = 50$ et d’écart-type $\sigma = 1,2$.
Calculer la probabilité qu’un pot de crème soit non conforme.
$\quad$ - La proportion de pots de crème non conformes est jugée trop importante. En modifiant la viscosité de la crème, on peut changer la valeur de l’écart-type de la variable aléatoire $X$, sans modifier son espérance $\mu = 50$. On veut réduire à $0,06$ la probabilité qu’un pot choisi au hasard soit non conforme.
On note $\sigma’$ le nouvel écart-type, et $Z$ la variable aléatoire égale à $\dfrac{X – 50}{\sigma’}$
a. Préciser la loi que suit la variable aléatoire $Z$.
$\quad$
b. Déterminer une valeur approchée du réel $u$ tel que $p(Z \leqslant u) = 0, 06$.
$\quad$
c. En déduire la valeur attendue de $\sigma’$.
$\quad$ - Une boutique commande à son fournisseur $50$ pots de cette nouvelle crème.
On considère que le travail sur la viscosité de la crème a permis d’atteindre l’objectif fixé et donc que la proportion de pots non conformes dans l’échantillon est $0,06$.
Soit $Y$ la variable aléatoire égale au nombre de pots non conformes parmi les $50$ pots reçus.
a. On admet que $Y$ suit une loi binomiale. En donner les paramètres.
$\quad$
b. Calculer la probabilité que la boutique reçoive deux pots non conformes ou moins de deux pots non conformes.
$\quad$
- Vues: 4562


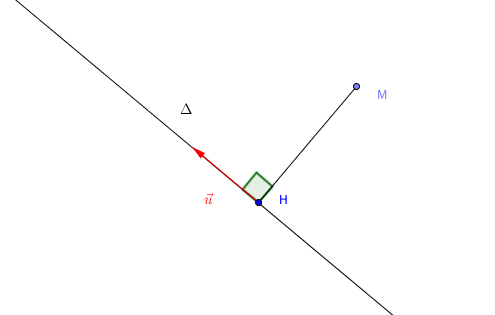
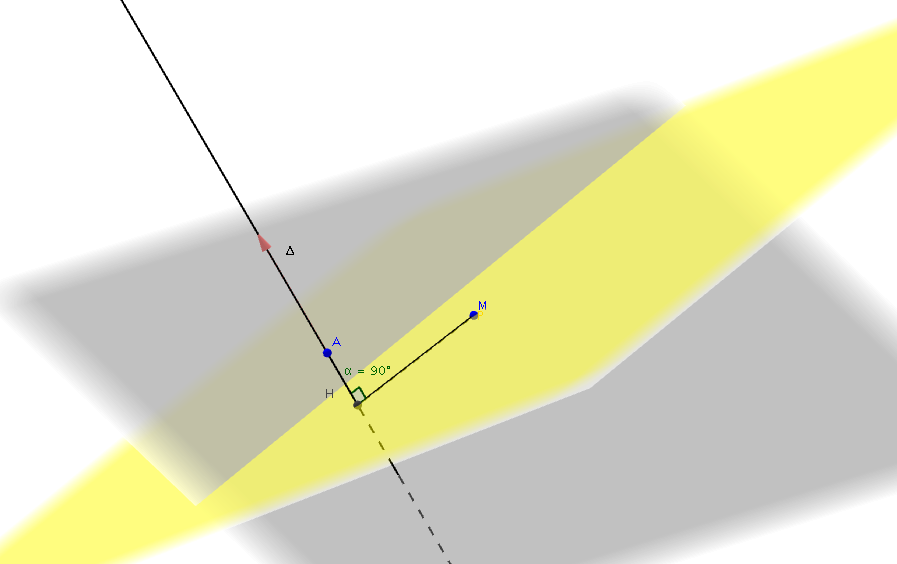 La distance du point $M$ à la droite $\Delta$ est égale à $MH$ où $H$ est le projeté orthogonal de $M$ sur $\Delta$.
La distance du point $M$ à la droite $\Delta$ est égale à $MH$ où $H$ est le projeté orthogonal de $M$ sur $\Delta$.