Baccalauréat S Antilles-Guyane 11 septembre 2013 - Correction de l'Exercice 4
Exercice 4 5 points
Les deux parties sont indépendantes.
Le robot Tom doit emprunter un pont sans garde-corps de 10 pas de long et de 2 pas de large. Sa démarche est très particulière :
- Soit il avance d'un pas tout droit ;
- Soit il se déplace en diagonale vers la gauche (déplacement équivalent à un pas vers la gauche et un pas tout droit) ;
- Soit il se déplace en diagonale vers la droite (déplacement équivalent à un pas vers la droite et un pas tout droit).
On suppose que ces trois types de déplacement sont aléatoires et équiprobables.
L'objectif de cet exercice est d'estimer la probabilité $p$ de l'évènement $S$ «Tom traverse le pont » c'est-à-dire «Tom n'est pas tombé dans l'eau et se trouve encore sur le pont au bout de 10 déplacements ».
Partie A : modélisation et simulation
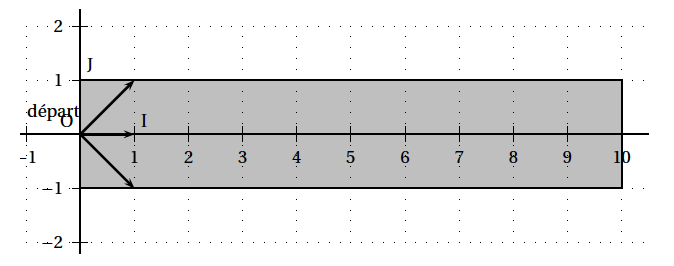
On schématise le pont par un rectangle dans le plan muni d'un repère orthonormé (O , I, J) comme l'indique la figure ci-dessous. On suppose que Tom se trouve au point de coordonnées (0 ; 0) au début de la traversée. On note $(x ; y)$ les coordonnées de la position de Tom après $x$ déplacements.
Figure
On a écrit l'algorithme suivant qui simule la position de Tom au bout de $x$ déplacements :
$$\begin{array}{|l|}\hline x, y, n \text{ sont des entiers}\\ \text{ Affecter à } x \text{ la valeur 0}\\ \text{ Affecter à } y \text{ la valeur 0}\\ \text{ Tant que } y \geqslant - 1 \text{ et } y \leqslant 1 \text{ et } x \leqslant 9\\ \hspace{1.5cm}\text{ Affecter à } n \text{ une valeur choisie au hasard entre - 1, 0 et 1}\\ \hspace{1.5cm}\text{ Affecter à } y \text{ la valeur } y + n\\ \hspace{1.5cm}\text{ Affecter à } x \text{ la valeur } x + 1 \\ \text{ Fin tant que } \\ \text{ Afficher } \ll \text{ la position de Tom est } (x\; ;\;y) \gg \\ \hline \end{array}$$
- On donne les couples suivants : $(-1 ; 1)$ ; (10 ; 0); (2 ; 4) ; (10 ; 2). Lesquels ont pu être obtenus avec cet algorithme ? Justifier la réponse. L’algorithme nous indique que nous sortons de la boucle quand $y < -1$,$y > 1$ ou $x>9$.
- Modifier cet algorithme pour qu'à la place de «la position de Tom est $(x ; y)$ », il affiche finalement «Tom a réussi la traversée » ou «Tom est tombé ». Si $(y \ge -1 \text{ et } y \le 1)$
La variable $x$ est initialisée à $0$ et est augmentée de $1$ à chaque tour de boucle. Elle ne prend donc que des valeurs positives.
$(-1;1)$ ne peut donc pas être obtenu.
$(10;0)$ correspond au cas où toutes les valeurs de $y$ sont comprises entre $-1$ et $1$. On sort donc de la boucle du fait de la condition sur $x$. Ce couple peut être obtenu.
$(2;4)$ ne peut être obtenu car la plus grande valeur que peut prendre $y$ est $3$ (et on sort de la boucle à ce moment là!).
$(10;2)$ peut être obtenu en étant parti précédemment su couple $(9;1)$ et ayant choisi $1$ pour $n$.
$\qquad$ alors Afficher « Tom a réussi la traversée ».
$\qquad$ sinon Afficher « Tom est tombé ».
Fin Si
Partie B
Pour tout $n$ entier naturel compris entre 0 et 10, on note :
$A_{n}$ l'évènement «après $n$ déplacements, Tom se trouve sur un point d'ordonnée $- 1$ ».
$B_{n}$ l'évènement «après $n$ déplacements, Tom se trouve sur un point d'ordonnée 0 ».
$C_{n}$ l'évènement «après $n$ déplacements, Tom se trouve sur un point d'ordonnée 1 ». On note $a_{n}, b_{n}, c_{n}$ les probabilités respectives des évènements $A_{n}, B_{n}, C_{n}$.
- Justifier que $a_{0} = 0, b_{0} = 1, c_{0} = 0$. Quand $n = 0$, Tom est au point de coordonnées $(0;0)$.
- Montrer que pour tout entier naturel $n$ compris entre $0$ et $9$, on a \[\left\{\begin{array}{l c l} a_{n+1} &=& \dfrac{a_{n} + b_{n}}{3}\\ b_{n+1} &=& \dfrac{a_{n} + b_{n} + c_{n}}{3} \end{array}\right.\]
On pourra s'aider d'un arbre pondéré. Si Tom se trouve sur un point d’ordonnée $-1$ après $(n+1)$ déplacements, c’est qu’il vient soit d’un point d’ordonnée $0$ (c’est-à-dire $B_n$) ou d’ordonnée $-1$ (c’est-à-dire $A_n$). - Calculer les probabilités $p\left(A_{1}\right),\: p\left(B_{1}\right)$ et $p\left(C_{1}\right)$. $p(A_1) = \dfrac{0+1}{3} = \dfrac{1}{3}$ et $p(B_1) = \dfrac{0 + 1 0}{3}=\dfrac{1}{3}$.
- Calculer la probabilité que Tom se trouve sur le pont au bout de deux déplacements. $p(A_2) = \dfrac{\dfrac{1}{3}+\dfrac{1}{3}}{3} = \dfrac{2}{9}$
- À l'aide d'un tableur, on a obtenu la feuille de calcul ci-contre qui donne des valeurs approchées de $a_{n},\: b_{n},\: c_{n}$ pour $n$ compris entre 0 et 10. Donner une valeur approchée à $0,001$ près de la probabilité que Tom traverse le pont (on pourra s'aider du tableau ci-dessous). $$\begin{array}{|c|c|c|c|}\hline n &a_{n} &b_{n} &c_{n} \\ \hline 0 &0 &1 &0\\ \hline 1 &0,333333 &0,333333 &0,333333\\ \hline 2 &0,222222 &0,333333 &0,222222\\ \hline 3 &0,185185 &0,259259 &0,185185\\ \hline 4 &0,148148 &0,209877 &0,148148\\ \hline 5 &0,119342 &0,168724 &0,119342\\ \hline 6 &0,096022 &0,135802 &0,096022\\ \hline 7 &0,077275 &0,109282 &0,077275\\ \hline 8 &0,062186 &0,087944 &0,062186\\ \hline 9 &0,050043 &0,070772 &0,050043\\ \hline 10 &0,040272 &0,056953 &0,040272\\ \hline \end{array} $$ Les trois événements $A_{10}$, $B_{10}$ et $C_{10}$ sont disjoints donc :
Donc $a_0 = 0$, $b_0 = 1$ et $c_0 = 0$.
Les trois types de déplacements sont équiprobables donc $a_{n+1} = \dfrac{a_n+b_n}{3}$.
Si Tom se trouve sur un point d’ordonnée $0$ après $(n+1)$ déplacements, c’est qu’il vient d’un point d’ordonnée $-1$ ($A_n$), d’ordonnée $0$ ($B_n$) ou d’ordonnée $1$ ($C_n$).
Les trois types de déplacements sont équiprobables donc $b_{n+1} = \dfrac{a_n+b_n+c_n}{3}$.
Pour la même raison que pour $a_{n+1}$, on a $c_{n+1} = \dfrac{c_n+b_n}{3}$.
Au premier déplacement, Tom ne peut pas tomber donc $p(C_1) = 1 – p(A_1) – p(B_1) = \dfrac{1}{3}$.
$p(B_2) = \dfrac{\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}}{3} = \dfrac{1}{3}$
$p(C_2) = \dfrac{\dfrac{1}{3}+\dfrac{1}{3}}{3} = \dfrac{2}{9}$.
$$p(A_{10} \cup B_{10} \cup C_{10}) = a_{10}+b_{10}+c_{10} \approx 0,137$$
- Vues: 44001
