Baccalauréat S Liban 31 mai 2019 - Correction Exercice 3
Correction de l'exercice 3 (6 points)
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
Dans un plan P, on considère un triangle ABC rectangle en A. Soit $d$ la droite orthogonale au plan P et passant par le point B. On considère un point D de cette droite distinct du point B.
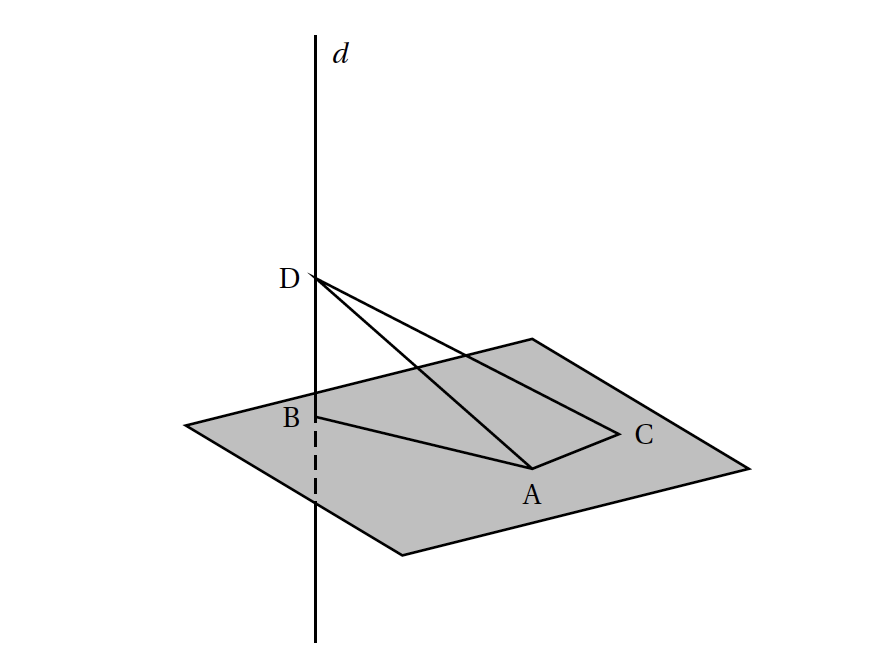
- Montrer que la droite (AC) est orthogonale au plan (BAD). La droite $d$ est orthogonale au plan $P$. Elle est donc orthogonale à toutes les droites de ce plan, en particulier à la droite $(AC)$.
- Montrer que le tétraèdre ABCD est un bicoin. >La droite $d$ est orthogonale à toutes les droites du plan $(ABC)$. Par conséquent les triangles $DBA$ et $DBC$ sont rectangles en $B$.
-
- Justifier que l'arête [CD] est la plus longue arête du bicoin ABCD. Le triangle $ABD$ est rectangle en $B$ donc $AD>AB$ et $AD>BD$.
- On note I le milieu de l'arête [CD]. Montrer que le point I est équidistant des 4 sommets du bicoin ABCD. $I$ est le milieu de l’hypoténuse $[DC]$ du triangle $ADC$ rectangle en $A$. C’est donc le centre du cercle circonscrit à ce triangle et $IA=IC=ID$.
Le triangle $ABC$ est rectangle en $A$ donc $BC>AB$ et $BC>AC$.
Le triangle $BCD$ est rectangle en $B$ donc $DC>BD$ et $DC>BC$.
Le triangle $ADC$ est rectangle en $A$ donc $DC>AD$ et $DC>AC$.
Ainsi $DC>AD>AB$, $DC>AD>AB$ et $DC>AC$.
L’arête $[CD]$ est bien la plus longue arête du bicoin $ABCD$.
$\quad$
$I$ est le milieu de l’hypoténuse $[DC]$ du triangle $BCD$ rectangle en $B$. C’est donc le centre du cercle circonscrit à ce triangle et $IB=IC=ID$.
Ainsi $IA=IB=IC=ID$ et le point $I$ est équidistant des $4$ sommets.
Le triangle $ABC$ est rectangle en $A$. Par conséquent la droite $(AC)$ est perpendiculaire à la droite $(AB)$.
Par construction les droites $(AB)$ et $d$ sont sécantes
La droite $(AC)$ est donc orthogonale à deux droites sécantes du plan $(BAD)$. Elle est donc orthogonale à ce plan.
$\quad$
On appelle bicoin un tétraèdre dont les quatre faces sont des triangles rectangles.
Par définition le triangle $ABC$ est rectangle en $A$.
Et
$\begin{align*} \vec{AD}.\vec{AC}&=\left(\vec{AB}+\vec{BD}\right).\vec{AC} \\
&=\vec{AB}.\vec{AC}+\vec{BD}.\vec{AC} \\
&=0+0 \\
&=0
\end{align*}$
Par conséquent le triangle $ADC$ est rectangle en $D$.
Remarque : Puisque la droite $(AC)$ est orthogonale au plan $(BAD)$, elle est en particulier orthogonale à la droite $(BD)$ et donc $\vec{BD}.\vec{AC}=0$.
$\quad$
Partie B
Dans un repère orthonormé de l'espace, on considère le point A$(3~;~1~;~ -5)$ et la droite $d$ de représentation paramétrique $\left\{\begin{array}{l c r} x &=& 2t + 1\\ y &= &- 2 t + 9\\ z&=&t - 3 \end{array}\right.$ où $t \in \mathbb R$.
- Déterminer une équation cartésienne du plan $P$ orthogonal à la droite $d$ et passant par le point A. Un vecteur directeur de la droite $d$ est $\vec{u}(2;-2;1)$.
- Montrer que le point d'intersection du plan $P$ et de la droite $d$ est le point B$(5~;~5~;~-1)$, En prenant $t=2$ dans la représentation paramétrique de la droite $d$ on retrouve les coordonnées du point $B$.
- Justifier que le point C$(7~;~3~;~-9)$ appartient au plan $P$ puis montrer que le triangle ABC est un triangle rectangle isocèle en A. $2\times 7-2\times 3-9+1=14-6-9+1=0$.
- Soit $t$ un réel différent de $2$ et $M$ le point de paramètre $t$ appartenant à la droite $d$.
- Justifier que le triangle AB$M$ est rectangle. les points $M$ et $B$ appartiennent à la droite $d$ orthogonale au plan $P$ et donc en particulier à la droite $(AB)$.
- Montrer que le triangle AB$M$ est isocèle en B si et seulement si le réel $t$ vérifie l'équation $t^2 - 4t = 0$. Le point $M$ a pour coordonnées $(2t+1;-2t+9;t-3)$ avec $t\neq 2$.
- En déduire les coordonnées des points $M_1$ et $M_2$ de la droite $d$ tels que les triangles rectangles AB$M_1$ et AB$M_2$ soient isocèles en B. Or $t^2-4t=0\iff t(t-4)=0\iff t=0$ ou $t=4$.
Ainsi le triangle $ABM$ est rectangle en $B$.
$\quad$
On a alors :
$\begin{align*} BM^2&=(2t+1-5)^2+(-2t+9-5)^2+(t-3+1)^2\\
&=(2t-4)^2+(-2t+4)^2+(t-2)^2\\
&=4t^2-16t+16+4t^2-16t+16+t^2-4t+4\\
&=9t^2-36t+36\end{align*}$
Par conséquent, $AB$ et $BM$ étant des nombres positifs on a :
$\begin{align*} AB=BM&\iff AB^2=BM^2 \\
&\iff 9t^2-36t+36=36 \\
&\iff 9t^2-36t=0\\
&\iff t^2-4t=0\end{align*}$
Le triangle $ABM$ est donc isocèle en $B$ si, et seulement si, le réel $t$ vérifie l’équation $t^2-4t=0$.
$\quad$
Si $t=0$ on obtient le point $M_1(1;9;-3)$
Si $t=4$ on obtient le point $M_2(9;1;1)$
D’après les deux questions précédentes, les triangles $ABM_1$ et $ABM_2$ sont rectangles et isocèles en $B$.
$\quad$
Ce vecteur est normal au plan $P$.
Une équation cartésienne de ce plan est donc de la forme $2x-2y+z+d=0$.
Le point $A$ appartient à ce plan.
Ainsi $6-2-5+d=0 \iff d=1$
Une équation cartésienne de $P$ est donc $2x-2y+z+1=0$.
$\quad$
Et $2\times 5-2\times 5-1+1=10-10=0$.
Le point $B$ appartient donc à la fois au plan $P$ et à la droite $d$.
La droite $d$, par définition, n’est pas incluse dans le plan $P$.
Ainsi le point $B(5;5;-1)$ est le point d’intersection du plan $P$ et de la droite $d$.
$\quad$
Le point $C$ appartient donc au plan $P$.
On a de plus :
$AB^2=(5-3)^2+(5-1)^2+(-1+5)^2=36$
$AC^2=(7-3)^2+(3-1)^2+(-9+5)^2=36$
$BC^2=(7-5)^2+(3-5)^2+(-9+1)^2=72$
Ainsi $AB^2+AC^2=BC^2$
D’après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $A$.
Puisque $AB^2=AC^2$, le triangle $ABC$ est également isocèle en $A$.
$\quad$
Partie C
On donne le point D(9 ; 1 ; 1) qui est un des deux points solutions de la question 4. c. de la partie B. Les quatre sommets du tétraèdre ABCD sont situés sur une sphère. En utilisant les résultats des questions des parties A et B précédentes, déterminer les coordonnées du centre de cette sphère et calculer son rayon.
On appelle $I$ le milieu de l’arête $[CD]$.
Ainsi le point $I$ a pour coordonnées $\left(\dfrac{7+9}{2};\dfrac{1+3}{2};\dfrac{1-9}{2}\right)$ soit $(8;2;-4)$.
D’après les parties A et B, le tétraèdre $ABCD$ est un bicoin et $I$ est équidistant des quatre sommets de ce bicoin.
$I$ est donc le centre de la sphère cherchée.
Le rayon de cette sphère est :
$\begin{align*} R&=IA \\
&=\sqrt{(8-3)^2+(1-2)^2+(-5+4)^2} \\
&=\sqrt{25+1+1}\\
&=\sqrt{27}\\
&=3\sqrt{3}\end{align*}$
Une figure :
- Vues: 78491
