Baccalauréat S Liban 31 mai 2019
Exercice 1 5 points
Le plan est muni d'un repère orthogonal (O, I, J).
- On considère la fonction $f$ définie sur l'intervalle ]0 ; 1] par \[f(x) = x(1 - \ln x)^2.\]
- Déterminer une expression de la fonction dérivée de $f$ et vérifier que pour tout $x \in ]0~;~1]$, $f'(x) = (\ln x + 1)(\ln x - 1)$.
- Étudier les variations de la fonction $f$ et dresser son tableau de variations sur l'intervalle $]0~;~1]$ (on admettra que la limite de la fonction $f$ en 0 est nulle).
On note $\Gamma$ la courbe représentative de la fonction $g$ définie sur l'intervalle $]0~;~1]$ par $g(x) = \ln x$. Soit $a$ un réel de l'intervalle $ ]0~;~1]$. On note $M_a$ le point de la courbe $\Gamma$ d'abscisse $a$ et $d_a$ la tangente à la courbe $\Gamma$ au point $M_a$. Cette droite $d_a$ coupe l'axe des abscisses au point $N_a$ et l'axe des ordonnées au point $P_a$ . On s'intéresse à l'aire du triangle O$N_aP_a$ quand le réel $a$ varie dans l'intervalle $]0~;~1]$.
- Dans cette question, on étudie le cas particulier où $a = 0,2$ et on donne la figure ci-dessous.
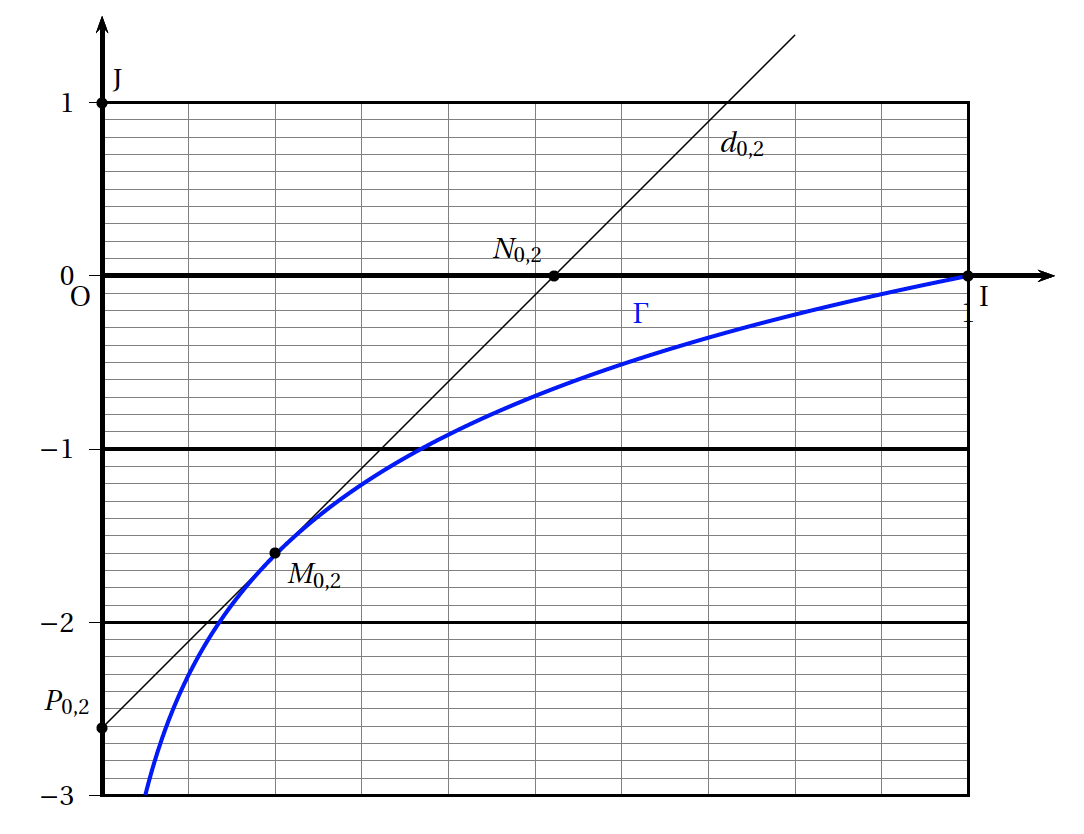
- Déterminer graphiquement une estimation de l'aire du triangle O$N_{0,2}P_{0,2}$ en unités d'aire.
- Déterminer une équation de la tangente $d_{0,2}$.
- Calculer la valeur exacte de l'aire du triangle O$N_{0,2}P_{0,2}$ . Dans ce qui suit, on admet que, pour tout réel $a$ de l'intervalle ]0 ; 1], l'aire du triangle O$N_aP_a$ en unités d'aire est donnée par $\mathcal{A}(a) = \dfrac{1}{2}a (1 - \ln a)^2$.
- À l'aide des questions précédentes, déterminer pour quelle valeur de $a$ l'aire $\mathcal{A}(a)$ est maximale. Déterminer cette aire maximale.
Correction de l'exercice 1 (5 points)
Le plan est muni d'un repère orthogonal (O, I, J).
- On considère la fonction $f$ définie sur l'intervalle $]0 ; 1]$ par \[f(x) = x(1 - \ln x)^2.\]
- Déterminer une expression de la fonction dérivée de $f$ et vérifier que pour tout $x \in ]0~;~1]$, $f'(x) = (\ln x + 1)(\ln x - 1)$. La fonction $f$ est dérivable sur $\mathbb R$ en tant que somme et produit de fonctions dérivables.
- Étudier les variations de la fonction $f$ et dresser son tableau de variations sur l'intervalle ]0~;~1] (on admettra que la limite de la fonction $f$ en 0 est nulle). Pour tout réel $x\in ]0;1]$ on a $\ln x\leq 0$ donc $\ln x-1\leq 0$.
Pour tout réel $x\in ]0;1]$ on a :
$\begin{align*} f'(x)&=\left(1-\ln x\right)^2+x\times \dfrac{-2}{x}\times \left(1-\ln x\right) \\
&=\left(1-\ln x\right)\left(\left(1-\ln x\right)-2\right)\\
&=\left(1-\ln x\right)\left(-1-\ln x\right) \\
&=-\left(1-\ln x\right)\left(1+\ln x\right)\\
&=\left(\ln x-1\right)\left(1+\ln x\right)\end{align*}$
$\quad$
$1+\ln x=0 \iff \ln x=-1 \iff x=\text{e}^{-1}$
et $1+\ln x>0 \iff \ln x>-1 \iff x>\text{e}^{-1}$.
Dressonss alors le tableau d signe de la dérivée :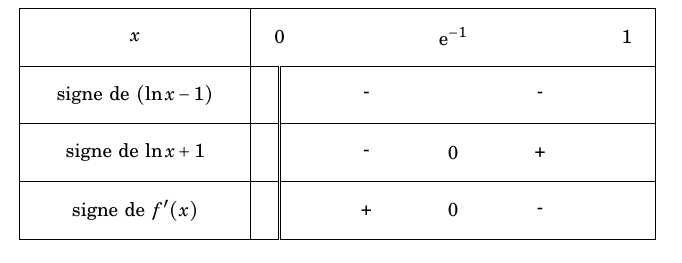
On obtient donc le tableau de variations suivant :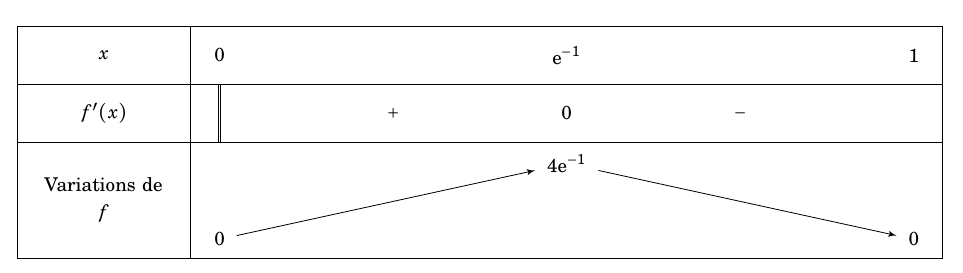
On note $\Gamma$ la courbe représentative de la fonction $g$ définie sur l'intervalle $]0~;~1]$ par $g(x) = \ln x$. Soit $a$ un réel de l'intervalle $ ]0~;~1]$. On note $M_a$ le point de la courbe $\Gamma$ d'abscisse $a$ et $d_a$ la tangente à la courbe $\Gamma$ au point $M_a$. Cette droite $d_a$ coupe l'axe des abscisses au point $N_a$ et l'axe des ordonnées au point $P_a$ . On s'intéresse à l'aire du triangle O$N_aP_a$ quand le réel $a$ varie dans l'intervalle $]0~;~1]$.
- Dans cette question, on étudie le cas particulier où $a = 0,2$ et on donne la figure ci-dessous.

- Déterminer graphiquement une estimation de l'aire du triangle O$N_{0,2}P_{0,2}$ en unités d'aire. Graphiquement l’aire du triangle $ON_{0,2}P_{0,2}$ est $\mathscr{A}(0,2)=\dfrac{0,52\times 2,6}{2}=0,676$ u.a.
- Déterminer une équation de la tangente $d_{0,2}$. Par définition de la fonction $\ln$ la fonction $g$ est dérivable sur l’intervalle $]0;1]$.
- Calculer la valeur exacte de l'aire du triangle O$N_{0,2}P_{0,2}$ . Dans ce qui suit, on admet que, pour tout réel $a$ de l'intervalle ]0 ; 1], l'aire du triangle O$N_aP_a$ en unités d'aire est donnée par $\mathcal{A}(a) = \dfrac{1}{2}a (1 - \ln a)^2$. Ainsi le point$P_{0,2}$ a pour coordonnées $\left(0;\ln(0,2)-1\right)$.
$\quad$
Une équation de la tangente $d_{0,2}$ est de la forme :
$y=g'(0,2)(x-0,2)+g(0,2)$
Or $g'(x)=\dfrac{1}{x}$ donc $g'(0,2)=5$.
Une équation de cette tangente est donc :
$y=5(x-0,2)+\ln(0,2)$ soit $y=5x+\ln(0,2)-1$.
$\quad$
et $5x+\ln(0,2)-1=0\iff x=\dfrac{1-\ln(0,2)}{5}$
Le point $N_{0,2}$ a pour coordonnées $\left(\dfrac{1-\ln(0,2)}{5};0\right)$.
L’aire du triangle $ON_{0,2}P_{0,2}$ est donc :
$\begin{align*} \mathscr{A}(0,2)&=\dfrac{\left|\dfrac{1-\ln(0,2)}{5}\times \left(\ln(0,2)-1\right)\right|}{2}\\
&=\dfrac{\left(1-\ln(0,2)\right)^2}{10}\end{align*}$
$\quad$ - À l'aide des questions précédentes, déterminer pour quelle valeur de $a$ l'aire $\mathcal{A}(a)$ est maximale. Déterminer cette aire maximale. On a ainsi $\mathscr{A}(a)=\dfrac{f(a)}{2}$.
D’après le tableau de variation de la fonction $f$, l’aire est donc maximale pour $a=\text{e}^{-1}$ et elle vaut alors $2\text{e}^{-1}$.
$\quad$
Exercice 2 4 points
Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$ d’unité 2 cm. On appelle $f$ la fonction qui, à tout point $M$, distinct du point O et d'affixe un nombre complexe $z$, associe le point $M’$ d'affixe $z’$ tel que \[z’ = - \dfrac{1}{z}.\]
- On considère les points A et B d'affixes respectives $z_{\text{A}} = - 1 + \text{i}$ et $z_{\text{B}} = \dfrac{1}{2} \text{e}^{\text{i}\frac{\pi}{3}}$.
- Déterminer la forme algébrique de l'affixe du point A$'$ image du point A par la fonction $f$.
- Déterminer la forme exponentielle de l'affixe du point B$'$ image du point B par la fonction $f$.
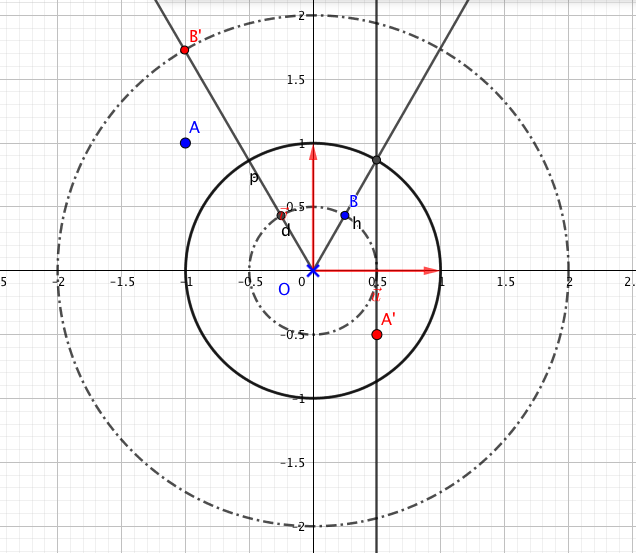
- Sur la copie, placer les points A, B, A$'$ et B$’$ dans le repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. Pour les points B et B$’$, on laissera les traits de construction apparents.
- Soit $r$ un réel strictement positif et $\theta$ un réel. On considère le complexe $z$ défini par $z = r\text{e}^{\text{i}\theta}$.
- Montrer que $z' = \dfrac{1}{r}\text{e}^{\text{i}(\pi - \theta)}$.
- Est-il vrai que si un point $M$, distinct de 0, appartient au disque de centre 0 et de rayon 1 sans appartenir au cercle de centre 0 et de rayon 1, alors son image $M’$ par la fonction $f$ est à l'extérieur de ce disque ? Justifier.
- Soit le cercle $\Gamma$ de centre K d'affixe $z_{\text{K}} = -\dfrac{1}{2}$ et de rayon $\dfrac{1}{2}$.
- Montrer qu'une équation cartésienne du cercle $\Gamma$ est $x^2 + x + y^2 = 0$.
- Soit $z = x + \text{i}y$ avec $x$ et $y$ non tous les deux nuls. Déterminer la forme algébrique de $z’$ en fonction de $x$ et $y$.
- Soit $M$ un point, distinct de O, du cercle $\Gamma$. Montrer que l'image $M’$ du point $M$ par la fonction $f$ appartient à la droite d'équation $x = 1$.
Correction de l'exercice 2 (5 points)
Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$ d’unité 2 cm. On appelle $f$ la fonction qui, à tout point $M$, distinct du point O et d'affixe un nombre complexe $z$, associe le point $M’$ d'affixe $z’$ tel que \[z’ = - \dfrac{1}{z}.\]
- On considère les points A et B d'affixes respectives $z_{\text{A}} = - 1 + \text{i}$ et $z_{\text{B}} = \dfrac{1}{2} \text{e}^{\text{i}\frac{\pi}{3}}$.
- Déterminer la forme algébrique de l'affixe du point A$'$ image du point A par la fonction $f$. On a :
- Déterminer la forme exponentielle de l'affixe du point B$'$ image du point B par la fonction $f$. On a :
- Sur la copie, placer les points A, B, A$'$ et B$’$ dans le repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. Pour les points B et B$’$, on laissera les traits de construction apparents.
$\begin{align*} z_{A’}&=-\dfrac{1}{-1+\text{i}}\\
&=-\dfrac{-1-\text{i}}{(-1)^2+1^2}\\
&=\dfrac{1+\text{i}}{2}\end{align*}$
$\quad$
$\begin{align*} z_{B’}&=-\dfrac{1}{\dfrac{1}{2}\text{e}^{\text{i} \pi/3}} \\
&=-2\text{e}^{-\text{i} \pi/3}\\
&=2\text{e}^{\text{i} \pi} \text{e}^{-\text{i} \pi/3} \\
&=2\text{e}^{2\text{i} \pi/3}\end{align*}$
$\quad$
- Soit $r$ un réel strictement positif et $\theta$ un réel. On considère le complexe $z$ défini par $z = r\text{e}^{\text{i}\theta}$.
- Montrer que $z' = \dfrac{1}{r}\text{e}^{\text{i}(\pi - \theta)}$. On a :
- Est-il vrai que si un point $M$, distinct de 0, appartient au disque de centre 0 et de rayon 1 sans appartenir au cercle de centre 0 et de rayon 1, alors son image $M’$ par la fonction $f$ est à l'extérieur de ce disque ? Justifier. Si un point $M$ appartient au disque de centre $O$ et de rayon $1$ sans appartenir au cercle de centre $O$ et de rayon $1$ alors $r<1$.
$\begin{align*} z’&=-\dfrac{1}{r\text{e}^{\text{i} \theta}} \\
&=-\dfrac{1}{r}\text{e}^{\text{i} \theta}\\
&=\text{e}^{\text{i} \pi}\times \dfrac{1}{r}\text{e}^{\text{i} \theta}\\
&=\dfrac{1}{r}\text{e}^{\text{i}(\pi-\theta)}\end{align*}$
$\quad$
Donc $\left|z’\right|=\dfrac{1}{r}>1$
Ainsi le point $M’$ est à l’extérieur de ce disque.
L’affirmation est donc vraie. - Soit le cercle $\Gamma$ de centre K d'affixe $z_{\text{K}} = -\dfrac{1}{2}$ et de rayon $\dfrac{1}{2}$.
- Montrer qu'une équation cartésienne du cercle $\Gamma$ est $x^2 + x + y^2 = 0$. Une équation cartésienne du cercle $\Gamma$ est :
- Soit $z = x + \text{i}y$ avec $x$ et $y$ non tous les deux nuls. Déterminer la forme algébrique de $z’$ en fonction de $x$ et $y$. Si $z=x+\text{i} y$ alors :
- Soit $M$ un point, distinct de O, du cercle $\Gamma$. Montrer que l'image $M’$ du point $M$ par la fonction $f$ appartient à la droite d'équation $x = 1$. Soit $M$ un point du cercle $\Gamma$ distinct du point $O$ on a donc $x^2+x+y^2=0$ et $(x;y)\neq (0,0)$.
$\begin{align*} &\left(x-\left(-\dfrac{1}{2}\right)\right)^2+y^2=\dfrac{1}{2^2}\\
\iff & x^2+x+\dfrac{1}{4}+y^2=\dfrac{1}{4} \\
\iff &x^2+x+y^2=0\end{align*}$
$\quad$
$\begin{align*} z’&=-\dfrac{1}{x+\text{i} y} \\
&=-\dfrac{x-\text{i} y}{x^2+y^2} \\
&=\dfrac{-x+\text{i} y}{x^2+y^2}
\end{align*}$
Ainsi $x=-\left(x^2+y^2\right)$.
Par conséquent
$\begin{align*} z’&=\dfrac{x^2+y^2+\text{i} y}{x^2+y^2} \\
&=1+\dfrac{y}{x^2+y^2}\text{i}\end{align*}$
Le point $M’$ appartient donc bien à la droite d’équation $x=1$.
Remarque : Une bonne question serait de se demander si tous les points de la droite sont atteints.
$\quad$
Exercice 3 6 points
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
Dans un plan P, on considère un triangle ABC rectangle en A. Soit $d$ la droite orthogonale au plan P et passant par le point B. On considère un point D de cette droite distinct du point B.
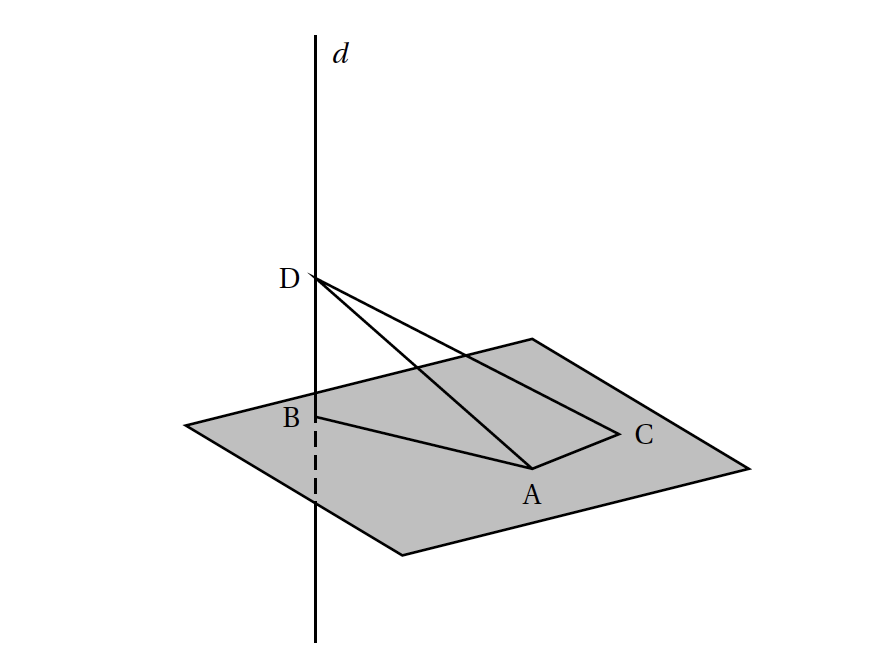
- Montrer que la droite (AC) est orthogonale au plan (BAD).
- Montrer que le tétraèdre ABCD est un bicoin.
-
- Justifier que l'arête [CD] est la plus longue arête du bicoin ABCD.
- On note I le milieu de l'arête [CD]. Montrer que le point I est équidistant des 4 sommets du bicoin ABCD.
On appelle bicoin un tétraèdre dont les quatre faces sont des triangles rectangles.
Partie B
Dans un repère orthonormé de l'espace, on considère le point A$(3~;~1~;~ -5)$ et la droite $d$ de représentation paramétrique $\left\{\begin{array}{l c r} x &=& 2t + 1\\ y &= &- 2 t + 9\\ z&=&t - 3 \end{array}\right.$ où $t \in \mathbb R$.
- Déterminer une équation cartésienne du plan $P$ orthogonal à la droite $d$ et passant par le point A.
- Montrer que le point d'intersection du plan $P$ et de la droite $d$ est le point B$(5~;~5~;~-1)$,
- Justifier que le point C$(7~;~3~;~-9)$ appartient au plan $P$ puis montrer que le triangle ABC est un triangle rectangle isocèle en A.
- Soit $t$ un réel différent de $2$ et $M$ le point de paramètre $t$ appartenant à la droite $d$.
- Justifier que le triangle AB$M$ est rectangle.
- Montrer que le triangle AB$M$ est isocèle en B si et seulement si le réel $t$ vérifie l'équation $t^2 - 4t = 0$.
- En déduire les coordonnées des points $M_1$ et $M_2$ de la droite $d$ tels que les triangles rectangles AB$M_1$ et AB$M_2$ soient isocèles en B.
Partie C
On donne le point D(9 ; 1 ; 1) qui est un des deux points solutions de la question 4. c. de la partie B. Les quatre sommets du tétraèdre ABCD sont situés sur une sphère. En utilisant les résultats des questions des parties A et B précédentes, déterminer les coordonnées du centre de cette sphère et calculer son rayon.
Correction de l'exercice 3 (6 points)
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
Dans un plan P, on considère un triangle ABC rectangle en A. Soit $d$ la droite orthogonale au plan P et passant par le point B. On considère un point D de cette droite distinct du point B.

- Montrer que la droite (AC) est orthogonale au plan (BAD). La droite $d$ est orthogonale au plan $P$. Elle est donc orthogonale à toutes les droites de ce plan, en particulier à la droite $(AC)$.
- Montrer que le tétraèdre ABCD est un bicoin. >La droite $d$ est orthogonale à toutes les droites du plan $(ABC)$. Par conséquent les triangles $DBA$ et $DBC$ sont rectangles en $B$.
-
- Justifier que l'arête [CD] est la plus longue arête du bicoin ABCD. Le triangle $ABD$ est rectangle en $B$ donc $AD>AB$ et $AD>BD$.
- On note I le milieu de l'arête [CD]. Montrer que le point I est équidistant des 4 sommets du bicoin ABCD. $I$ est le milieu de l’hypoténuse $[DC]$ du triangle $ADC$ rectangle en $A$. C’est donc le centre du cercle circonscrit à ce triangle et $IA=IC=ID$.
Le triangle $ABC$ est rectangle en $A$ donc $BC>AB$ et $BC>AC$.
Le triangle $BCD$ est rectangle en $B$ donc $DC>BD$ et $DC>BC$.
Le triangle $ADC$ est rectangle en $A$ donc $DC>AD$ et $DC>AC$.
Ainsi $DC>AD>AB$, $DC>AD>AB$ et $DC>AC$.
L’arête $[CD]$ est bien la plus longue arête du bicoin $ABCD$.
$\quad$
$I$ est le milieu de l’hypoténuse $[DC]$ du triangle $BCD$ rectangle en $B$. C’est donc le centre du cercle circonscrit à ce triangle et $IB=IC=ID$.
Ainsi $IA=IB=IC=ID$ et le point $I$ est équidistant des $4$ sommets.
Le triangle $ABC$ est rectangle en $A$. Par conséquent la droite $(AC)$ est perpendiculaire à la droite $(AB)$.
Par construction les droites $(AB)$ et $d$ sont sécantes
La droite $(AC)$ est donc orthogonale à deux droites sécantes du plan $(BAD)$. Elle est donc orthogonale à ce plan.
$\quad$
On appelle bicoin un tétraèdre dont les quatre faces sont des triangles rectangles.
Par définition le triangle $ABC$ est rectangle en $A$.
Et
$\begin{align*} \vec{AD}.\vec{AC}&=\left(\vec{AB}+\vec{BD}\right).\vec{AC} \\
&=\vec{AB}.\vec{AC}+\vec{BD}.\vec{AC} \\
&=0+0 \\
&=0
\end{align*}$
Par conséquent le triangle $ADC$ est rectangle en $D$.
Remarque : Puisque la droite $(AC)$ est orthogonale au plan $(BAD)$, elle est en particulier orthogonale à la droite $(BD)$ et donc $\vec{BD}.\vec{AC}=0$.
$\quad$
Partie B
Dans un repère orthonormé de l'espace, on considère le point A$(3~;~1~;~ -5)$ et la droite $d$ de représentation paramétrique $\left\{\begin{array}{l c r} x &=& 2t + 1\\ y &= &- 2 t + 9\\ z&=&t - 3 \end{array}\right.$ où $t \in \mathbb R$.
- Déterminer une équation cartésienne du plan $P$ orthogonal à la droite $d$ et passant par le point A. Un vecteur directeur de la droite $d$ est $\vec{u}(2;-2;1)$.
- Montrer que le point d'intersection du plan $P$ et de la droite $d$ est le point B$(5~;~5~;~-1)$, En prenant $t=2$ dans la représentation paramétrique de la droite $d$ on retrouve les coordonnées du point $B$.
- Justifier que le point C$(7~;~3~;~-9)$ appartient au plan $P$ puis montrer que le triangle ABC est un triangle rectangle isocèle en A. $2\times 7-2\times 3-9+1=14-6-9+1=0$.
- Soit $t$ un réel différent de $2$ et $M$ le point de paramètre $t$ appartenant à la droite $d$.
- Justifier que le triangle AB$M$ est rectangle. les points $M$ et $B$ appartiennent à la droite $d$ orthogonale au plan $P$ et donc en particulier à la droite $(AB)$.
- Montrer que le triangle AB$M$ est isocèle en B si et seulement si le réel $t$ vérifie l'équation $t^2 - 4t = 0$. Le point $M$ a pour coordonnées $(2t+1;-2t+9;t-3)$ avec $t\neq 2$.
- En déduire les coordonnées des points $M_1$ et $M_2$ de la droite $d$ tels que les triangles rectangles AB$M_1$ et AB$M_2$ soient isocèles en B. Or $t^2-4t=0\iff t(t-4)=0\iff t=0$ ou $t=4$.
Ainsi le triangle $ABM$ est rectangle en $B$.
$\quad$
On a alors :
$\begin{align*} BM^2&=(2t+1-5)^2+(-2t+9-5)^2+(t-3+1)^2\\
&=(2t-4)^2+(-2t+4)^2+(t-2)^2\\
&=4t^2-16t+16+4t^2-16t+16+t^2-4t+4\\
&=9t^2-36t+36\end{align*}$
Par conséquent, $AB$ et $BM$ étant des nombres positifs on a :
$\begin{align*} AB=BM&\iff AB^2=BM^2 \\
&\iff 9t^2-36t+36=36 \\
&\iff 9t^2-36t=0\\
&\iff t^2-4t=0\end{align*}$
Le triangle $ABM$ est donc isocèle en $B$ si, et seulement si, le réel $t$ vérifie l’équation $t^2-4t=0$.
$\quad$
Si $t=0$ on obtient le point $M_1(1;9;-3)$
Si $t=4$ on obtient le point $M_2(9;1;1)$
D’après les deux questions précédentes, les triangles $ABM_1$ et $ABM_2$ sont rectangles et isocèles en $B$.
$\quad$
Ce vecteur est normal au plan $P$.
Une équation cartésienne de ce plan est donc de la forme $2x-2y+z+d=0$.
Le point $A$ appartient à ce plan.
Ainsi $6-2-5+d=0 \iff d=1$
Une équation cartésienne de $P$ est donc $2x-2y+z+1=0$.
$\quad$
Et $2\times 5-2\times 5-1+1=10-10=0$.
Le point $B$ appartient donc à la fois au plan $P$ et à la droite $d$.
La droite $d$, par définition, n’est pas incluse dans le plan $P$.
Ainsi le point $B(5;5;-1)$ est le point d’intersection du plan $P$ et de la droite $d$.
$\quad$
Le point $C$ appartient donc au plan $P$.
On a de plus :
$AB^2=(5-3)^2+(5-1)^2+(-1+5)^2=36$
$AC^2=(7-3)^2+(3-1)^2+(-9+5)^2=36$
$BC^2=(7-5)^2+(3-5)^2+(-9+1)^2=72$
Ainsi $AB^2+AC^2=BC^2$
D’après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $A$.
Puisque $AB^2=AC^2$, le triangle $ABC$ est également isocèle en $A$.
$\quad$
Partie C
On donne le point D(9 ; 1 ; 1) qui est un des deux points solutions de la question 4. c. de la partie B. Les quatre sommets du tétraèdre ABCD sont situés sur une sphère. En utilisant les résultats des questions des parties A et B précédentes, déterminer les coordonnées du centre de cette sphère et calculer son rayon.
On appelle $I$ le milieu de l’arête $[CD]$.
Ainsi le point $I$ a pour coordonnées $\left(\dfrac{7+9}{2};\dfrac{1+3}{2};\dfrac{1-9}{2}\right)$ soit $(8;2;-4)$.
D’après les parties A et B, le tétraèdre $ABCD$ est un bicoin et $I$ est équidistant des quatre sommets de ce bicoin.
$I$ est donc le centre de la sphère cherchée.
Le rayon de cette sphère est :
$\begin{align*} R&=IA \\
&=\sqrt{(8-3)^2+(1-2)^2+(-5+4)^2} \\
&=\sqrt{25+1+1}\\
&=\sqrt{27}\\
&=3\sqrt{3}\end{align*}$
Une figure :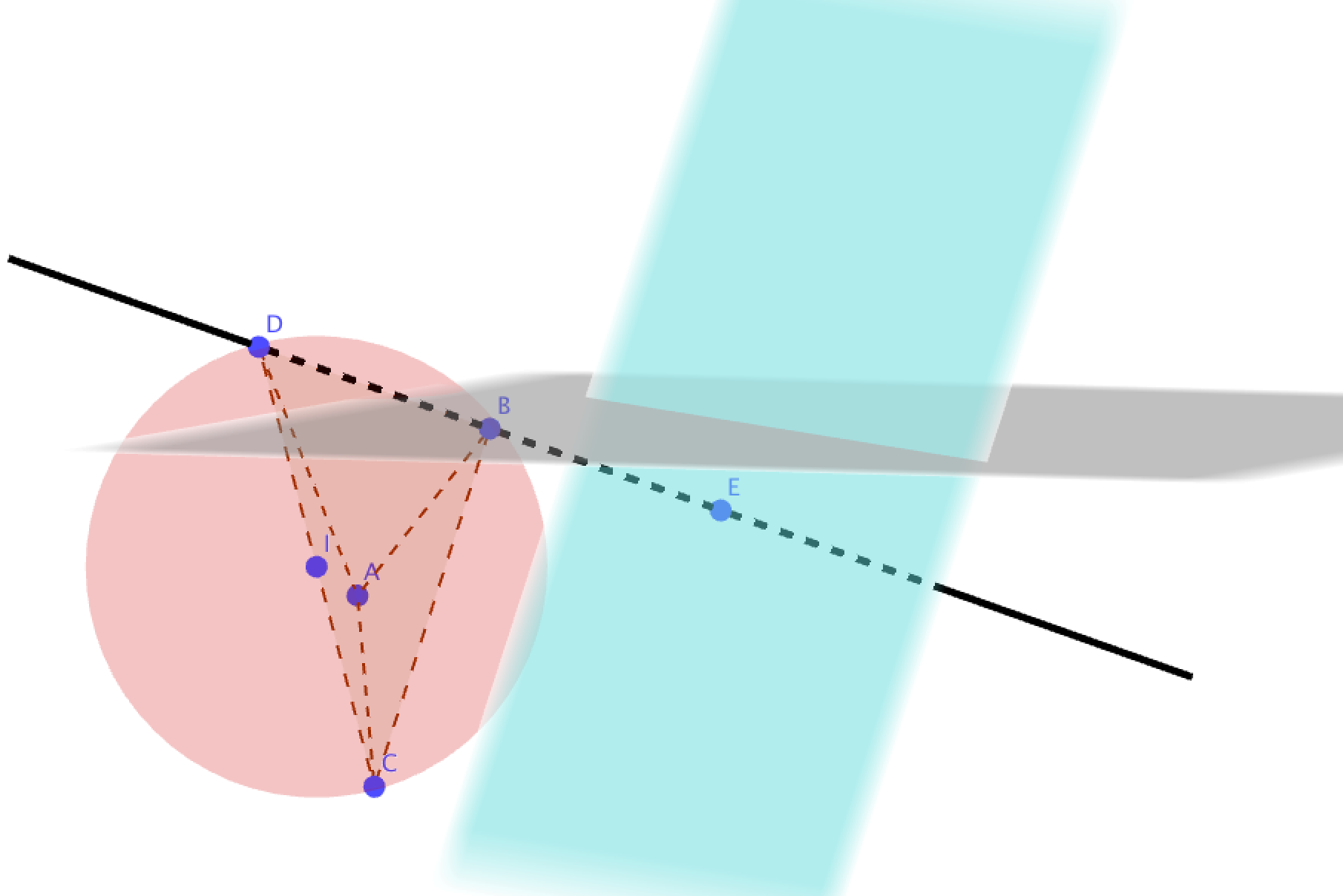
Exercice 4 5 points
Les deux parties 1 et 2 sont indépendantes.
Chaque semaine, un agriculteur propose en vente directe à chacun de ses clients un panier de produits frais qui contient une seule bouteille de jus de fruits. Dans un esprit de développement durable, il fait le choix de bouteilles en verre incassable et demande à ce que chaque semaine, le client rapporte sa bouteille vide. On suppose que le nombre de clients de l'agriculteur reste constant. Une étude statistique réalisée donne les résultats suivants :
- à l'issue de la première semaine, la probabilité qu'un client rapporte la bouteille de son panier est $0,9$;
- si le client a rapporté la bouteille de son panier une semaine, alors la probabilité qu'il ramène la bouteille du panier la semaine suivante est $0,95$ ;
- si le client n'a pas rapporté la bouteille de son panier une semaine, alors la probabilité qu'il ramène la bouteille du panier la semaine suivante est $0,2$.
On choisit au hasard un client parmi la clientèle de l'agriculteur. Pour tout entier naturel $n$ non nul, on note $R_n$ l'évènement « le client rapporte la bouteille de son panier de la $n$-ième semaine ».
-
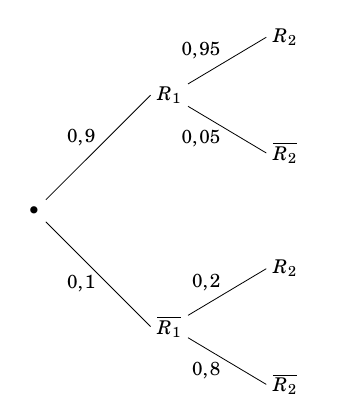
- Modéliser la situation étudiée pour les deux premières semaines à l'aide d'un arbre pondéré qui fera intervenir les évènements $R_1$ et $R_2$.
- Déterminer la probabilité que le client rapporte ses bouteilles des paniers de la première et de la deuxième semaine.
- Montrer que la probabilité que le client rapporte la bouteille du panier de la deuxième semaine est égale à $0,875$.
- Sachant que le client a rapporté la bouteille de son panier de la deuxième semaine, quelle est la probabilité qu'il n'ait pas rapporté la bouteille de son panier de la première semaine ? On arrondira le résultat à $10^{-3}$.
- Pour tout entier naturel $n$ non nul, on note $r_n$ la probabilité que le client rapporte la bouteille du panier de la $n$-ième semaine. On a alors $r_n = p\left(R_n\right)$.
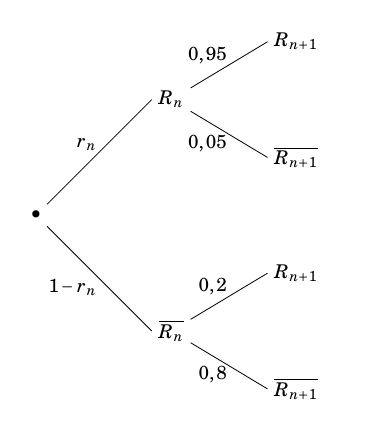
- Recopier et compléter l'arbre pondéré (aucune justification n'est attendue) :
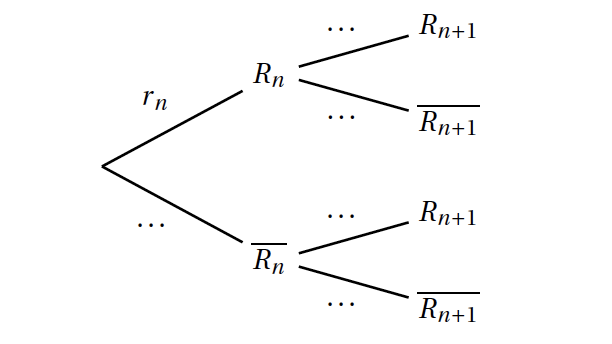
- Justifier que pour tout entier naturel $n$ non nul, $r_{n+1} = 0,75 r_n + 0,2$.
- Démontrer que pour tout entier naturel $n$ non nul, $r_n = 0,1 \times 0,75^{n-1} + 0,8$.
- Calculer la limite de la suite $\left(r_n\right)$. Interpréter le résultat dans le contexte de l'exercice.
- Recopier et compléter l'arbre pondéré (aucune justification n'est attendue) :
Correction de l'exercice 4 5 points
Les deux parties 1 et 2 sont indépendantes.
Chaque semaine, un agriculteur propose en vente directe à chacun de ses clients un panier de produits frais qui contient une seule bouteille de jus de fruits. Dans un esprit de développement durable, il fait le choix de bouteilles en verre incassable et demande à ce que chaque semaine, le client rapporte sa bouteille vide. On suppose que le nombre de clients de l'agriculteur reste constant. Une étude statistique réalisée donne les résultats suivants :
- à l'issue de la première semaine, la probabilité qu'un client rapporte la bouteille de son panier est $0,9$;
- si le client a rapporté la bouteille de son panier une semaine, alors la probabilité qu'il ramène la bouteille du panier la semaine suivante est $0,95$ ;
- si le client n'a pas rapporté la bouteille de son panier une semaine, alors la probabilité qu'il ramène la bouteille du panier la semaine suivante est $0,2$.
On choisit au hasard un client parmi la clientèle de l'agriculteur. Pour tout entier naturel $n$ non nul, on note $R_n$ l'évènement « le client rapporte la bouteille de son panier de la $n$-ième semaine ».
-
- Modéliser la situation étudiée pour les deux premières semaines à l'aide d'un arbre pondéré qui fera intervenir les évènements $R_1$ et $R_2$.
- Déterminer la probabilité que le client rapporte ses bouteilles des paniers de la première et de la deuxième semaine. On veut calculer
- Montrer que la probabilité que le client rapporte la bouteille du panier de la deuxième semaine est égale à $0,875$. D’après la formule des probabilités totales on a :
- Sachant que le client a rapporté la bouteille de son panier de la deuxième semaine, quelle est la probabilité qu'il n'ait pas rapporté la bouteille de son panier de la première semaine ? On arrondira le résultat à $10^{-3}$. On veut calculer :
$\begin{align*} P\left(R_1\cap R_2\right)&=0,9\times 0,95 \\
&=0,855\end{align*}$
$\quad$
$\begin{align*} P\left(R_2\right)&=P\left(R_1\cap R_2\right)+P\left(\overline{R_1}\cap R_2\right)\\
&=0,855+0,1\times 0,2\\
&=0,875\end{align*}$
$\quad$
$\begin{align*} P_{R_2}\left(R_1\right)&=\dfrac{P\left(R_2\cap \overline{R_1}\right)}{P\left(R_2\right)} \\
&=\dfrac{0,02}{0,875} \\
&\approx 0,023\end{align*}$
$\quad$ - Modéliser la situation étudiée pour les deux premières semaines à l'aide d'un arbre pondéré qui fera intervenir les évènements $R_1$ et $R_2$.
- Pour tout entier naturel $n$ non nul, on note $r_n$ la probabilité que le client rapporte la bouteille du panier de la $n$-ième semaine. On a alors $r_n = p\left(R_n\right)$.
- Recopier et compléter l'arbre pondéré (aucune justification n'est attendue) :

- Justifier que pour tout entier naturel $n$ non nul, $r_{n+1} = 0,75 r_n + 0,2$. D’après la formule des probabilités totales on a :
- Démontrer que pour tout entier naturel $n$ non nul, $r_n = 0,1 \times 0,75^{n-1} + 0,8$. Montrons ce résultat par récurrence sur $n$.
- Calculer la limite de la suite $\left(r_n\right)$. Interpréter le résultat dans le contexte de l'exercice. On a $-1<0,75<1$ donc $\lim\limits_{n\to +\infty} 0,75^{n-1}=0$.
$\begin{align*} r_{n+1}&=P\left(R_{n+1}\right) \\
&=P\left(R_n\cap R_{n+1}\right)+P\left(\overline{R_n}\cap R_{n+1}\right) \\
&=0,95r_n+0,2\left(1-r_n\right) \\
&=0,95r_n+0,2-0,2r_n \\
&=0,75r_n+0,2\end{align*}$
$\quad$
Initialisation : Si $n=1$ alors $0,1\times 0,75^0+0,8=0,9=r_1$.
La propriété est donc vraie au rang $1$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$. Donc $r_n=0,1\times 0,75^{n-1}+0,8$.
Montrons qu’elle est encore vraie au rang suivant, c’est-à-dire que $r_{n+1}=0,1\times 0,75^n+0,8$.
$\begin{align*} r_{n+1}&=0,75r_n+0,2\\
&=0,75\left(0,1\times 0,75^n+0,8\right)+0,2\\
&=0,1\times 0,75^n+0,6+0,2\\
&=0,1\times 0,75^n+0,8\end{align*}$
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $1$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ non nul on a $r_n=0,1\times 0,75^{n-1}+0,8$.
$\quad$
Par conséquent $\lim\limits_{n\to +\infty} r_n=0,8$.
Sur le long terme, la probabilité que le client rapporte la bouteille du panier est $0,8$.
$\quad$ - Recopier et compléter l'arbre pondéré (aucune justification n'est attendue) :
Spécialité 5 points
Dans un jardin public, un artiste doit installer une œuvre aquatique commandée par la mairie. Cette œuvre sera constituée de deux bassins A et B ainsi que d'une réserve filtrante R. Au départ, les deux bassins contiennent chacun 100 litres d'eau. Un système de canalisations devra alors permettre de réaliser, toutes les heures et dans cet ordre, les transferts d'eau suivants:
- dans un premier temps, la moitié du bassin A se vide dans la réserve R ;
- ensuite, les trois quarts du bassin B se vident dans le bassin A ;
- enfin, on rajoute $200$ litres d'eau dans le bassin A et $300$~litres d'eau dans le bassin B.
Une étude de faisabilité du projet amène à étudier la contenance des deux bassins A et B qui est à prévoir pour éviter tout débordement.
On modélise les quantités d'eau des deux bassins A et B à l'aide de deux suites $\left(a_n\right)$ et $\left(b_n\right)$ : plus précisément pour tout entier naturel $n$, on note $a_n$ et $b_n$ les quantités d'eau en centaines de litres qui seront respectivement contenues dans les bassins A et B au bout de $n$ heures. On suppose pour cette étude mathématique que les bassins sont a priori suffisamment grands pour qu'il n'y ait pas de débordement.
Pour tout entier naturel $n$, on note $U_n$ la matrice colonne $U_n = \begin{pmatrix}a_n\\b_n \end{pmatrix}$. Ainsi $U_0 = \begin{pmatrix}1\\1 \end{pmatrix}$.
- Justifier que, pour tout entier naturel $n$, $U_{n+1} = MU_n + C$ où $M = \begin{pmatrix}0,5&0,75\\0&0,25\end{pmatrix}$ et $C = \begin{pmatrix}2\\3\end{pmatrix}$.
- On considère la matrice $P = \begin{pmatrix}1 &3\\0&- 1\end{pmatrix}$.
- Calculer $P^2$. En déduire que la matrice $P$ est inversible et préciser sa matrice inverse.
- Montrer que $PMP$ est une matrice diagonale $D$ que l'on précisera.
- Calculer $PDP$.
- Démontrer par récurrence que, pour tout entier naturel $n$,\, $M^n = PD^nP$.
On admet par la suite que pour tout entier naturel $n$, $M_n = \begin{pmatrix}0,5^n& 3 \times 0,5^n - 3 \times 0,25^n\\0&0,25^n\end{pmatrix}$.
- Montrer que la matrice $X = \begin{pmatrix}10\\4\end{pmatrix}$ vérifie $X = MX + C$.
- Pour tout entier naturel $n$, on définit la matrice $V_n$ par $V_n = U_n - X$.
- Montrer que tout entier naturel $n$, $V_{n+1} = MV_n$.
- On admet que, pour tout entier naturel non nul $n$, $V_n = M^n V_0$.
Montrer que pour tout entier naturel non nul $n$, $U_n = \begin{pmatrix}-18 \times 0,5^n + 9 \times 0,25^n + 10\\- 3 \times 0,25^n + 4\end{pmatrix}$.
-
- Montrer que la suite $\left(b_n\right)$ est croissante et majorée. Déterminer sa limite.
- Déterminer la limite de la suite $\left(a_n\right)$.
- On admet que la suite $\left(a_n\right)$ est croissante. En déduire la contenance des deux bassins A et B qui est à prévoir pour la faisabilité du projet, c'est-à-dire pour éviter tout débordement.
Correction de l'exercice de Spécialité 5 points
Dans un jardin public, un artiste doit installer une œuvre aquatique commandée par la mairie. Cette œuvre sera constituée de deux bassins A et B ainsi que d'une réserve filtrante R. Au départ, les deux bassins contiennent chacun 100 litres d'eau. Un système de canalisations devra alors permettre de réaliser, toutes les heures et dans cet ordre, les transferts d'eau suivants:
- dans un premier temps, la moitié du bassin A se vide dans la réserve R ;
- ensuite, les trois quarts du bassin B se vident dans le bassin A ;
- enfin, on rajoute $200$ litres d'eau dans le bassin A et $300$~litres d'eau dans le bassin B.
Une étude de faisabilité du projet amène à étudier la contenance des deux bassins A et B qui est à prévoir pour éviter tout débordement.
On modélise les quantités d'eau des deux bassins A et B à l'aide de deux suites $\left(a_n\right)$ et $\left(b_n\right)$ : plus précisément pour tout entier naturel $n$, on note $a_n$ et $b_n$ les quantités d'eau en centaines de litres qui seront respectivement contenues dans les bassins A et B au bout de $n$ heures. On suppose pour cette étude mathématique que les bassins sont a priori suffisamment grands pour qu'il n'y ait pas de débordement.
Pour tout entier naturel $n$, on note $U_n$ la matrice colonne $U_n = \begin{pmatrix}a_n\\b_n \end{pmatrix}$. Ainsi $U_0 = \begin{pmatrix}1\\1 \end{pmatrix}$.
- Justifier que, pour tout entier naturel $n$, $U_{n+1} = MU_n + C$ où $M = \begin{pmatrix}0,5&0,75\\0&0,25\end{pmatrix}$ et $C = \begin{pmatrix}2\\3\end{pmatrix}$. Pour tout entier naturel $n$ on a :
- On considère la matrice $P = \begin{pmatrix}1 &3\\0&- 1\end{pmatrix}$.
- Calculer $P^2$. En déduire que la matrice $P$ est inversible et préciser sa matrice inverse. On a :
- Montrer que $PMP$ est une matrice diagonale $D$ que l'on précisera. On a :
- Calculer $PDP$. On a :
- Démontrer par récurrence que, pour tout entier naturel $n$,\, $M^n = PD^nP$. On note $I_2$ la matrice identité de taille $2$.
$P^2=\begin{pmatrix} 1&3-3\\0&1\end{pmatrix}=\begin{pmatrix}1&0\\0&1\end{pmatrix}$.
Ainsi $P$ est inversible et $P^{-1}=P$.
$\quad$
$\begin{align*} PMP&=\begin{pmatrix}1&3\\0&-1\end{pmatrix}\begin{pmatrix}0,5&0,75\\0&0,25\end{pmatrix}\begin{pmatrix}1&3\\0&-1\end{pmatrix}\\
&=\begin{pmatrix}0,5&1,5\\0&-0,25\end{pmatrix}\begin{pmatrix}1&3\\0&-1\end{pmatrix}\\
&=\begin{pmatrix}0,5&0\\0&0,25\end{pmatrix}\end{align*}$
La matrice $D=PMP$ est donc une matrice diagonale et $D=\begin{pmatrix}0,5&0\\0&0,25\end{pmatrix}$.
$\quad$
$\begin{align*} PMP=D&\iff PPMP=PD \quad (*)\\
&\iff MP=PD\\
&\iff MPP=PDP \quad (*)\\
&\iff M=PDP\end{align*}$
$(*)$ Puisque $P^{-1}=P$.
$\quad$
Initialisation : Si $n=0$ on a $PD^0P=PI_2P=P^2=I_2$.
Et $M^0=I_2$
Donc $M^0=PD^0P$.
La propriété est vraie au rang $0$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $M^n=PD^nP$.
Montrons que la propriété est vraie au rang suivant, c’est-à-dire que $M^{n+1}=PD^{n+1}P$.
$\begin{align*} M^{n+1}&=M^nM\\
&=PD^nPPDP\\
&=PD^nDP\\
&=PD^{n+1}P\end{align*}$
La propriété est donc vraie au rang $n$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Pour tout entier naturel $n$ on a $M^n=PD^nP$.
$\quad$
$a_{n+1}=0,5a_n+0,75b_n+2$ et $b_{n+1}=0,25b_n+3$.
Ainsi :
$\begin{pmatrix}a_{n+1}\\b_{n+1}\end{pmatrix}=\begin{pmatrix}0,5&0,75\\0&0,25\end{pmatrix}\begin{pmatrix}a_n\\b_n\end{pmatrix}+\begin{pmatrix}2\\3\end{pmatrix}$.
Soit $U_{n+1}=MU_n+C$.
$\quad$
On admet par la suite que pour tout entier naturel $n$, $M_n = \begin{pmatrix}0,5^n& 3 \times 0,5^n - 3 \times 0,25^n\\0&0,25^n\end{pmatrix}$.
- Montrer que la matrice $X = \begin{pmatrix}10\\4\end{pmatrix}$ vérifie $X = MX + C$. On a :
- Pour tout entier naturel $n$, on définit la matrice $V_n$ par $V_n = U_n - X$.
- Montrer que tout entier naturel $n$, $V_{n+1} = MV_n$. Pour tout entier naturel $n$ on a :
- On admet que, pour tout entier naturel non nul $n$, $V_n = M^n V_0$.
Montrer que pour tout entier naturel non nul $n$, $U_n = \begin{pmatrix}-18 \times 0,5^n + 9 \times 0,25^n + 10\\- 3 \times 0,25^n + 4\end{pmatrix}$. On a $V_0=U_0-X=\begin{pmatrix} -9\\-3\end{pmatrix}$
$\begin{align*} V_{n+1}&=U_{n+1}-X \\
&=MU_n+C-\left(MX+C\right)\\
&=MU_n+C-MX-C\\
&=MU_n-MX\\
&=M\left(U_n-X\right)\\
&=MV_n\end{align*}$
$\quad$
Et pour tout entier naturel $n$ :
$\begin{align*} U_n&=V_n+X\\
&=M^nV_0+X \\
&=\begin{pmatrix} -9\times 0,5^n-9\times 0,5^n+9\times 0,25^n\\-3\times 0,25^n\end{pmatrix}+\begin{pmatrix} 10\\4\end{pmatrix} \\
&=\begin{pmatrix}-18\times 0,5^n+9\times 0,25^n+10\\-3\times 0,25^n+4\end{pmatrix}\end{align*}$
$\quad$ -
- Montrer que la suite $\left(b_n\right)$ est croissante et majorée. Déterminer sa limite. Pour tout entier naturel $n$ on a donc $b_n=-3\times 0,25^n+4$.
- Déterminer la limite de la suite $\left(a_n\right)$. $-1<0,25<1$ donc $\lim\limits_{n \to +\infty} 0,25^n=0$ et $-1<0,5<1$ donc $\lim\limits_{n \to +\infty} 0,5^n=0$.
- On admet que la suite $\left(a_n\right)$ est croissante. En déduire la contenance des deux bassins A et B qui est à prévoir pour la faisabilité du projet, c'est-à-dire pour éviter tout débordement. D’après les deux résultats précédents, il faut donc prévoir un bassin A de $1~000$ litres et un bassin B de $400$ litres.
Donc
$\begin{align*} b_{n+1}-b_n&=-3\times 0,25^{n+1}+4+3\times 0,25^n-4\\
&=-3\times 0,25^n\times (0,25-1) \\
&=2,25\times 0,25^n\\
&>0\end{align*}$
La suite $\left(b_n\right)$ est donc croissante.
De plus $b_n-4=-3\times 0,25^n<0$.
La suite $\left(b_n\right)$ est donc croissante et majorée par $4$; elle converge donc.
Or $-1<0,25<1$ donc $\lim\limits_{n \to +\infty} 0,25^n=0$.
Donc $\lim\limits_{n\to +\infty} b_n=4$.
$\quad$
Par conséquent $\lim\limits_{n\to +\infty} a_n=10$.
$\quad$
$\quad$
$\begin{align*} MX+C&=\begin{pmatrix}8\\1\end{pmatrix}+\begin{pmatrix}2\\3\end{pmatrix} \\
&=\begin{pmatrix}10\\4\end{pmatrix} \\
&=X\end{align*}$
$\quad$
- Vues: 83033
