Baccalauréat STI2D Métropole - La Réunion - 18 juin 2019 - Correction Exercice 2

Page 4 sur 8: Correction Exercice 2

Correction de l'exercice 2 (7 points)

Suites et fonctions

Suites et fonctions Les parties A et B de cet exercice sont indépendantes.
Le conservatoire des espaces naturels d'une région s’occupe d’une zone protégée de 1800 hectares. Depuis plusieurs années, il surveille le domaine d’extension d’une plante invasive. Cette plante inhabituelle, d’origine exotique, devient envahissante et cause une régression de la biodiversité. Si le conservatoire constate qu’à la fin d’une année l’aire de la surface occupée par la plante dépasse 80 hectares, cette plante fera alors l’objet d’un plan d’élimination progressive à partir de l’année suivante.

Partie A

1. Des relevés de la surface occupée par cette plante ont été effectués sur le terrain, en fin d'année, de 2015 à 2018 : $$\begin{array}{|c|c|c|c|c|} \hline \text{Année } & 2015 & 2016 & 2017& 2018 \\ \hline \text{Surface en hectares (ha) } &63 & 66,2 & 69,5&73 \\ \hline \end{array} $$ Le conservatoire estime que l’aire de la surface occupée par cette plante a augmenté de 5% environ chaque année.
   Vérifier que cette estimation est cohérente avec les relevés pris sur le terrain.
Pour augmenter de 5%, on multiplie par 1+5%= 1,05. On a ainsi :
• $63 \times 1,05= 66,15\approx 66,2$
• $66,2 \times 1,05= 69,51\approx 69,5$
• $69,5 \times 1,05= 72,975\approx 73$
Cette estimation est donc cohérente avec les relevés pris sur le terrain.
2. On considère qu’à partir de l’année 2018 la surface occupée par la plante augmente chaque année de 5%.
   Expliquer alors pourquoi la décision de commencer l'élimination de la plante devrait être prise à la fin de l'année 2020 par le conservatoire.
La surface occupée par la plante augmente chaque année de 5%.
• En 2018, la surface occupée est 73 ha.
• En 2019, la surface occupée est $73\times 1,05\approx 76,65$ ha
• En 2020, la surface occupée est $76,65\times 1,05\approx 80,5$ ha
La surface occupée par plante dépasse 80 hectares, cette plante fera alors l’objet d’un plan d’élimination progressive à partir de l’année suivante.
3. Le conservatoire décide de mettre en oeuvre un plan d’élimination progressive. Ce plan prévoit d’éliminer la plante, par arrachage ou par brûlage thermique, sur une surface de 10 hectares à chaque fin d’année, à partir de l’année 2021.
   Pour tout entier naturel $n$, on désigne par $P_n$ l’aire de la surface occupée par la plante, exprimée en hectares, en fin d’année « 2020 + $n$ », en prenant $P_0 = 80,5$.
   1. Montrer que $P_1 = 74,525$.
   $P_1 = 1,05P_0-10=74,525$ En effet, on passe de $P_0$ à $P_1$ en multipliant par 1,05( augmentation de 5%), puis on retranche 10, car on arrache ou on brûle , sur une surface de 10 hectares à chaque fin d’année.
   2. Justifier que pour tout entier naturel $n$, on a : $P_{n+1} = 1,05P_n - 10$.
   Comme $P_n$ est l’aire de la surface occupée par la plante, exprimée en hectares, en fin d’année « 2020 + $n$ », on a après augmentation de 5 % sur une année, il y aura $(1+0,05)P_n=1,05P_n$.
   Puis on brûle , sur une surface de 10 hectares à chaque fin d’année : $01,05P_n-10$
   D'où le résultat: $P_{n+1} = 1,05P_n - 10.$
   3. Donner une valeur arrondie de $P_2$ à $10^{-3}$ près.
   $$\begin{array}{rl} P_2&=1,05P_1-10 \\ & =1,05 \times74,525-10\\ &=68,25125 \end{array}$$ A $10^{-3}$ près $P_2\approx 68,251$
   4. Pourquoi la suite $\left (P_n\right )$ n’est-elle pas géométrique?
   Si la suite $\left (P_n\right )$ était géométrique de raison $q$ alors $P_1=qP_0$ et $P_2=qP_1$ .
   On doit avoir $\dfrac{P_1}{P_0}=\dfrac{P_2}{P_1}$
   Or $\dfrac{P_1}{P_0}=\dfrac{74,525}{80,5}\approx 0,926$ et $\dfrac{P_2}{P_1}=\dfrac{68,25125}{74,525}\approx 0,916$
   La suite $\left (P_n\right )$ n’est pas géométrique.
4. Le conservatoire décidera de mettre fin au plan d’élimination dès que l’aire de la surface occupée par la plante sera inférieure à 6 hectares. Recopier et compléter l’algorithme ci-contre pour qu'à la fin de son exécution, la variable $n$ contienne le nombre d’années de mise en oeuvre du plan. $$ \begin{array}{|l|}\hline N\gets 0\\ P \gets 80,5\\ \text{Tant que }\:P \geq 6\\ \hspace{0.8cm}U \gets \ldots\\ \hspace{0.8cm}N \gets \ldots~~~~~ \\ \text{Fin Tant que}\\ \hline \end{array} $$
$$ \begin{array}{|l|}\hline N\gets 0\\ P \gets 80,5\\ \text{Tant que }\:P \geq 6\\ \hspace{0.8cm}P \gets 1,05P-10\\ \hspace{0.8cm}N \gets N+1 \\ \text{Fin Tant que}\\ \hline \end{array} $$
5. À la fin de quelle année le plan d’élimination prendra-t-il fin?
Plusieurs méthodes sont possibles :
On saisit l'algorithme ci-dessus sur une calculatrice
On obtient $P_{10}\approx 5,35$
On peut également utiliser le mode suite de la calculatrice :
Le plan d’élimination prendra fin à la fin de l'année 2030.

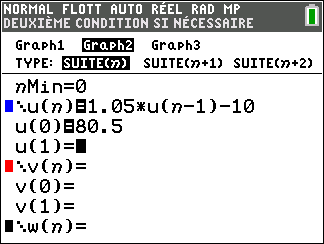
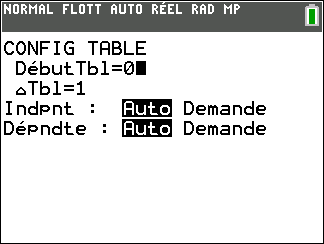
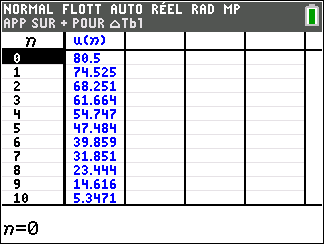
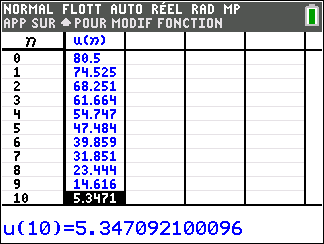
Partie B

Le logo utilisé par le conservatoire pour la communication est constitué de deux feuilles symétriques l’une de l’autre, dessinées ci-dessous. Soient les fonctions $f$ et $g$ définies sur l’intervalle $[0,1; 1,25]$ par $f(x) =\dfrac{0,2}{x}$ et $g(x) = -x^2 + 0,2x +1$. On note $\mathcal{C}_f$ et $\mathcal{C}_g$ les courbes représentatives de ces fonctions tracées dans le repère orthonormé ci-contre.

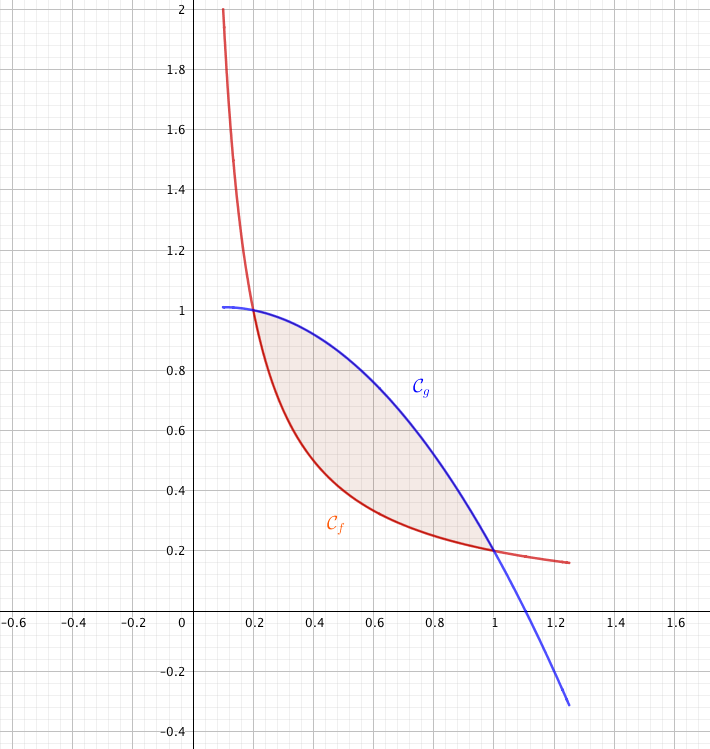
La feuille gauche du logo correspond à la partie grisée du plan, délimitée par ces deux courbes.

1. Vérifier par le calcul que 0,2 est une solution de l’équation $f(x) = g(x)$.
$f(0,2)=\dfrac{0,2}{0,2}=1$
$g(0,2) = -0,2^2 + 0,2\times 0,2 +1= -0,04+0,04+1=1$
0,2 est donc une solution de l’équation $f(x) = g(x)$.
2. Déterminer graphiquement la seconde solution de cette équation.
Graphiquement $A(1;1)$ est un point commun des courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ , donc 1 est donc une autre solution de l’équation $f(x) = g(x)$.
3. 1. Interpréter graphiquement l’intégrale $I = \displaystyle\int_{0,2}^1 g(x) \text{d} x$.
   La fonction $g$ est positive sur l’intervalle $[0,1; 1,25]$; en effet $\mathcal{C}_g$ est située au-dessus de laxe des abscisses sur l’intervalle $[0,1; 1,25]$.
   Donc l’intégrale $I = \displaystyle\int_{0,2}^1 g(x) \text{d} x$ représente l'aire, exprimée en unités d'aires, du domaine délimité par la courbe $\mathcal{C}_g$, l'axe des abscisses et les droites d'équations $x=0,2$ et $x=1$.
   2. Donner une valeur approchée de cette intégrale à $10^{-2}$ près.
   Ayant $g(x) = -x^2 + 0,2x +1$, on déduit $G$ une primitive de $g$: $$G(x)=-\dfrac{x^3}{3}+0,2\dfrac{x^2}{2}+x$$ $$\begin{array}{rlrl} I &= \displaystyle\int_{0,2}^1 g(x) \text{d} x &&\\ & =\left [ -\dfrac{x^3}{3}+0,2\dfrac{x^2}{2}+x \right ]_{0,2}^1&&\\ &&&\\ G(1)&= -\dfrac{1^3}{3}+0,2+0,2\dfrac{1^2}{2}+1& G(0,2)&=-\dfrac{0,2^3}{3}+0,2\dfrac{0,2^2}{2}+0,2\\ &=1,1-\dfrac{1}{3}&&\approx 0,7667\\ &\approx 0,2013&& \end{array}$$ $I = \displaystyle\int_{0,2}^1 g(x) \text{d} x=G(1)-G(0,2)\approx 0,57$
4. 1. Montrer que la fonction $F$ définie sur l’intervalle $[0,1; 1,25]$ par $F(x) = \frac{1}{5} \ln (x)$ est une primitive sur l’intervalle $[0,1; 1,25]$ de la fonction $f$.
   Il suffit de vérifier que la dérivée de$F$ est $f$.
   Comme $F(x) = \frac{1}{5} \ln (x)$, on déduit $F'(x)= \frac{1}{5}\times \frac{1}{x}=0,2\times \frac{1}{x}=\frac{0,2}{x}=f(x)$
   La fonction $F$ définie sur l’intervalle $[0,1; 1,25]$ par $F(x) = \frac{1}{5} \ln (x)$ est une primitive sur l’intervalle $[0,1; 1,25]$ de la fonction $f$.
   2. Calculer la valeur exacte de l’intégrale $J = \displaystyle\int_{0,2}^1 f(x) \text{d} x$.
$$\begin{array}{rlrl} J &= \displaystyle\int_{0,2}^1 f(x) \text{d} x&&\\ & =\left [ \frac{1}{5} \ln (x) \right ]_{0,2}^1&&\\ &&&\\ F(1)&= \frac{1}{5} \ln (1)& F(0,2)&=\frac{1}{5} \ln (0,2) \\ &=0&& = \frac{1}{5} \ln \left (\frac{1}{5}\right )\\ &&&=-\frac{\ln 5}{5} \\ && \end{array}$$ $$J = \displaystyle\int_{0,2}^1 f(x) \text{d} x =F(1)-F(0,2)= \frac{\ln 5}{5}$$
5. On admet que la courbe $\mathcal{C}_g$ est située au-dessus de la courbe $\mathcal{C}_f$ sur l’intervalle $[0,2 ; 1]$.
   L’unité choisie sur chacun des axes est de 2,5 cm.
   En déduire, au cm$^2$ près, une valeur approchée de l’aire totale du logo.
La courbe $\mathcal{C}_g$ est située au-dessus de la courbe $\mathcal{C}_f$ sur l’intervalle $[0,2 ; 1]$; l'aire du domaie délimité par les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ associée à l’intervalle $[0,2 ; 1]$ vaut, en unités d'aire : $$\begin{array}{rl} A&= \displaystyle\int_{0,2}^1 \left ( g(x)- f(x)\right ) \text{d} x \\ & = \displaystyle\int_{0,2}^1 \ g(x) \text{d} x - \displaystyle\int_{0,2}^1 \ f(x) \text{d} x \\ &= I-J\\ &\approx 0,57- \frac{\ln 5}{5}\\ &\approx 0,25\: \text{u.a.}\\ \end{array}$$ Ici l'unité d'aire vaut $2,5\times 2,5 =6,25$ cm$^2$ Donc l'aire du logo,cm$^2$ vaut $2A\approx 2\times 0,25\times 6,25\approx 3,125$ cm$^2$.
Au cm$^2$ près, l’aire totale du logo vaut environ 3 cm$^2$.