Baccalauréat STI2D Métropole - La Réunion - 18 juin 2019

 

Exercice 1 4 points

QCM Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes,une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée.
Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Indiquer sur la copie le numéro de la question et la réponse correspondante choisie.

1. Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$.
   On note $z_A$ l'affixe d'un point $A$ appartenant au cercle de centre $O$ et de rayon 4. La partie réelle de $z_A$ est positive et sa partie imaginaire est égale à 2.
   1. $4\text{e}^{-\text{i}\frac{\pi}{6}}$
   2. $-4\text{e}^{\text{i}\frac{\pi}{6}}$
   3. $4\text{e}^{\text{i}\frac{\pi}{6}}$
   4. $-4 \text{e}^{-\text{i}\frac{\pi}{6}}$
2. Le nombre -3 est solution de l'équation :
   1. $\ln (x)=-\ln(3)$
   2. $ \ln\left (\text{e}^x\right )=-3$
   3. $ \text{e}^{\ln(x)} =3$
   4. $\text{e}^x=3$
3. On considère la fonction $g$ définie sur $\left ]-\frac{1}{2}~;~+ \infty\right [$ par $g(x) = \dfrac{\text{e}^x}{2x+1})$.
   La fonction $g$ est dérivable sur l'intervalle $\left ]-\frac{1}{2}~;~+ \infty\right [$ et sa fonction dérivée est définie sur $\left ]-\frac{1}{2}~;~+ \infty\right [$ par :
   1. $g'(x) =\dfrac{\text{e}^x}{2}$
   2. $g'(x) = \dfrac{\text{e}^x}{\left (2x+1\right )^2})$
   3. $g'(x) = \dfrac{(2x+3)\text{e}^x}{\left (2x+1\right )^2})$
   4. aucune des réponses précédentes
4. On considère l'équation différentielle $y" + 4y = 0$ dans laquelle $y$ est une fonction de la variable réelle $x$ définie et deux fois dérivable sur $\mathbb R$.
   Une fonction $f$, solution de cette équation différentielle qui vérifie $f(0) = 1$ est définie sur $\mathbb R$ par :
   1. $f(x)=\text{e}^{2x} $
   2. $f(x)=\cos(2x)$
   3. $f(x)=\sin(2x)$
   4. $f(x)=\cos(4x)$

 

Correction de l'exercice 1 (4 points)

QCM Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes,une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée.
Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Indiquer sur la copie le numéro de la question et la réponse correspondante choisie.

1. Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$.
   On note $z_A$ l'affixe d'un point $A$ appartenant au cercle de centre $O$ et de rayon 4. La partie réelle de $z_A$ est positive et sa partie imaginaire est égale à 2.
   1. $4\text{e}^{-\text{i}\frac{\pi}{6}}$
   2. $-4\text{e}^{\text{i}\frac{\pi}{6}}$
   3. $4\text{e}^{\text{i}\frac{\pi}{6}}$
   4. $-4 \text{e}^{-\text{i}\frac{\pi}{6}}$
Une figure :

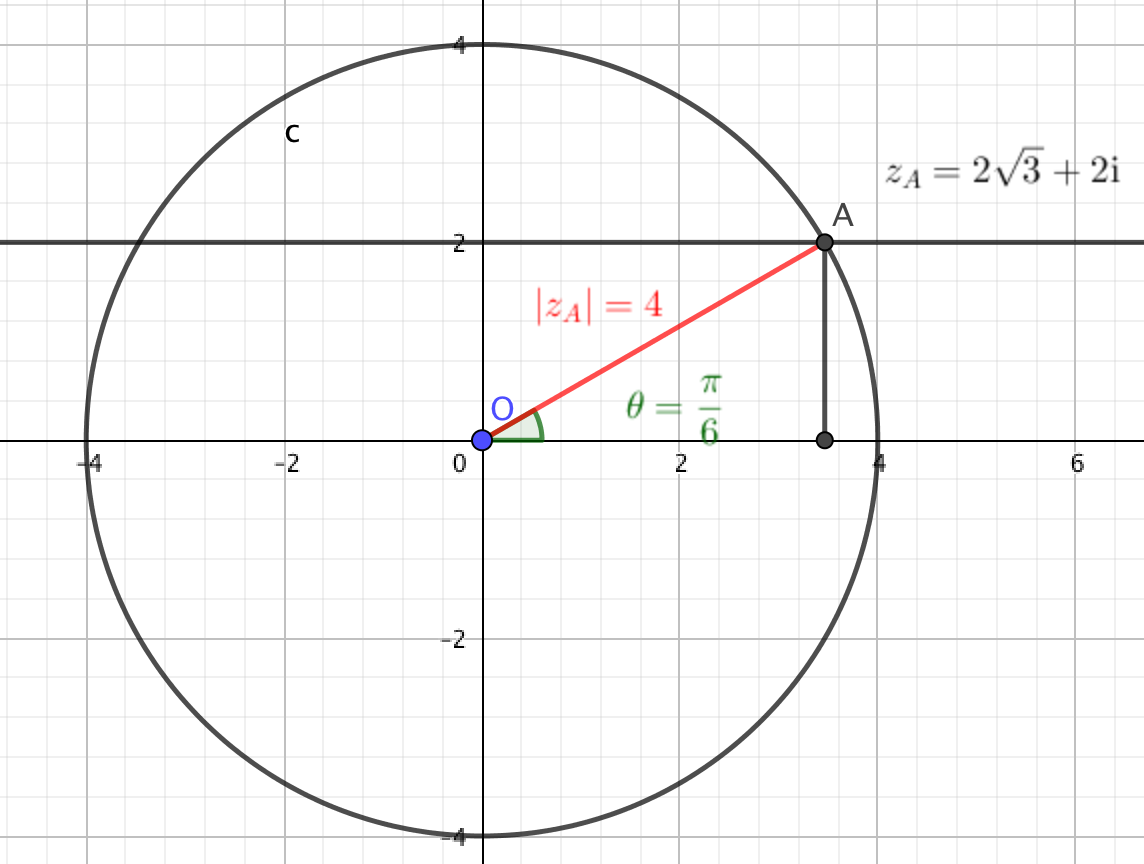
On a ainsi $z_A=2\sqrt 3 +2\text{i}$. $$\begin{array}{cc} \text{Module} & \text{Argument} \\ \begin{array}{rl|rl} |z |&=\sqrt{a^2+b^2} \\ & =\sqrt{ \left (2\sqrt 3\right )^2+2^2}\\ &=\sqrt {16}\\ &= 4 \end{array}& \left\lbrace \begin{array}{l} \cos \theta=\frac{a}{r}~=\frac{2\sqrt 3}{4}=\frac{\sqrt 3}{2}\\ ~\sin \theta=\frac{b}{r}~= \frac{2}{4}= \frac{1}{2} \end{array} \right.\\ &\text{ Donc } \theta = \frac{\pi}{6} \text{ convient } \end{array}$$ $$z= 2 \sqrt 3+2\text{i}= 4\left(\cos\left(\frac{\pi}{6} \right) +i\sin \left(\frac{\pi}{6} \right) \right) =4\text{e}^{\text{i}\frac{\pi}{6}}$$
Bonne réponse : c
2. Le nombre -3 est solution de l'équation :
   1. $\ln (x)=-\ln(3)$
   2. $ \ln\left (\text{e}^x\right )=-3$
   3. $ \text{e}^{\ln(x)} =3$
   4. $\text{e}^x=3$
$ \ln\left (\text{e}^x\right )=-3 \iff x=-3$ car pour tout réel $x$ on a : $ \ln\left (\text{e}^x\right )=x$
Bonne réponse : b
3. On considère la fonction $g$ définie sur $\left ]-\frac{1}{2}~;~+ \infty\right [$ par $g(x) = \dfrac{\text{e}^x}{2x+1})$.
   La fonction $g$ est dérivable sur l'intervalle $\left ]-\frac{1}{2}~;~+ \infty\right [$ et sa fonction dérivée est définie sur $\left ]-\frac{1}{2}~;~+ \infty\right [$ par :
   1. $g'(x) =\dfrac{\text{e}^x}{2}$
   2. $g'(x) = \dfrac{\text{e}^x}{\left (2x+1\right )^2})$
   3. $g'(x) = \dfrac{(2x+3)\text{e}^x}{\left (2x+1\right )^2})$
   4. aucune des réponses précédentes

$g$ est dérivable comme quotient de deux fonctions dérivables dont le dénominateur ne s'annule pas sur $\left ]-\frac{1}{2}~;~+ \infty\right [$. $g=\dfrac{u}{v}$ d'où $g'=\dfrac{u'v-v'u}{v^2}$ avec pour tout réel $x$, dans $\left ]-\frac{1}{2}~;~+ \infty\right [$ : $\left\{ \begin{array}{l} u(x)~ = \text{e}^x\\ v(x)~ =2x+1 \end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ = \text{e}^x \\ v'(x)~ = 2\end{array}\right.$ $$ \begin{array}{cl} g'(x)&=\dfrac{\text{e}^x(2x+1)-2\text{e}^x }{\left (2x+1\right )^2}\\ & = \dfrac{\text{e}^x(2x+1-2) }{\left (2x+1\right )^2}\\ &= \dfrac{\text{e}^x(2x-1) }{\left (2x+1\right )^2}\\ \end{array} $$ Bonne réponse : d on obtient $g'(x) = \dfrac{(2x-1)\text{e}^x}{\left (2x+1\right )^2} $
4. On considère l'équation différentielle $y" + 4y = 0$ dans laquelle $y$ est une fonction de la variable réelle $x$ définie et deux fois dérivable sur $\mathbb R$.
   Une fonction $f$, solution de cette équation différentielle qui vérifie $f(0) = 1$ est définie sur $\mathbb R$ par :
   1. $f(x)=\text{e}^{2x} $
   2. $f(x)=\cos(2x)$
   3. $f(x)=\sin(2x)$
   4. $f(x)=\cos(4x)$
L'équation différentielle $y" + 4y = 0$ est du type $y"+\omega^2 y=0$ où $\omega =2$.
Les solutions de l'équation différentielle $y"+4y=0$ sont les fonctions définies sur $\mathbb R$ par $x\longmapsto A \cos⁡ (2⁢x)+B\sin⁡ (2x)$ où $A$ et $B$ sont deux constantes réelles quelconques.
$f(0) = 1\iff A \cos⁡ (0)+B\sin⁡ (0)=1\iff A =1$ En choisissant $A=1$ et $B=0$, la fonction $f$ définie pour tout réel $x$ par $f⁡(x)= \cos⁡ (2⁢x)$ est une solution de l'équation différentielle $y″+4y=0 $ qui vérifie $f(0) = 1$

Bonne réponse : b

Exercice 2 (7 points)

Suites et fonctions Les parties A et B de cet exercice sont indépendantes.
Le conservatoire des espaces naturels d'une région s’occupe d’une zone protégée de 1800 hectares. Depuis plusieurs années, il surveille le domaine d’extension d’une plante invasive. Cette plante inhabituelle, d’origine exotique, devient envahissante et cause une régression de la biodiversité. Si le conservatoire constate qu’à la fin d’une année l’aire de la surface occupée par la plante dépasse 80 hectares, cette plante fera alors l’objet d’un plan d’élimination progressive à partir de l’année suivante.

Partie A

1. Des relevés de la surface occupée par cette plante ont été effectués sur le terrain, en fin d'année, de 2015 à 2018 : $$\begin{array}{|c|c|c|c|c|} \hline \text{Année } & 2015 & 2016 & 2017& 2018 \\ \hline \text{Surface en hectares (ha) } &63 & 66,2 & 69,5&73 \\ \hline \end{array} $$ Le conservatoire estime que l’aire de la surface occupée par cette plante a augmenté de 5% environ chaque année.
   Vérifier que cette estimation est cohérente avec les relevés pris sur le terrain.
2. On considère qu’à partir de l’année 2018 la surface occupée par la plante augmente chaque année de 5%.
   Expliquer alors pourquoi la décision de commencer l'élimination de la plante devrait être prise à la fin de l'année 2020 par le conservatoire.
3. Le conservatoire décide de mettre en oeuvre un plan d’élimination progressive. Ce plan prévoit d’éliminer la plante, par arrachage ou par brûlage thermique, sur une surface de 10 hectares à chaque fin d’année, à partir de l’année 2021.
   Pour tout entier naturel $n$, on désigne par $P_n$ l’aire de la surface occupée par la plante, exprimée en hectares, en fin d’année « 2020 + $n$ », en prenant $P_0 = 80,5$.
   1. Montrer que $P_1 = 74,525$.
   2. Justifier que pour tout entier naturel $n$, on a : $P_{n+1} = 1,05P_n - 10$.
   3. Donner une valeur arrondie de $P_2$ à $10^{-3}$ près.
   4. Pourquoi la suite $\left (P_n\right )$ n’est-elle pas géométrique?
4. Le conservatoire décidera de mettre fin au plan d’élimination dès que l’aire de la surface occupée par la plante sera inférieure à 6 hectares. Recopier et compléter l’algorithme ci-contre pour qu'à la fin de son exécution, la variable $n$ contienne le nombre d’années de mise en oeuvre du plan. $$ \begin{array}{|l|}\hline N\gets 0\\ P \gets 80,5\\ \text{Tant que }\:P \geq 6\\ \hspace{0.8cm}U \gets \ldots\\ \hspace{0.8cm}N \gets \ldots~~~~~ \\ \text{Fin Tant que}\\ \hline \end{array} $$
5. À la fin de quelle année le plan d’élimination prendra-t-il fin?

Partie B

 

Le logo utilisé par le conservatoire pour la communication est constitué de deux feuilles symétriques l’une de l’autre, dessinées ci-dessous. Soient les fonctions $f$ et $g$ définies sur l’intervalle $[0,1; 1,25]$ par $f(x) =\dfrac{0,2}{x}$ et $g(x) = -x^2 + 0,2x +1$. On note $\mathcal{C}_f$ et $\mathcal{C}_g$ les courbes représentatives de ces fonctions tracées dans le repère orthonormé ci-contre.

On admet que ces deux courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ se coupent en deux points.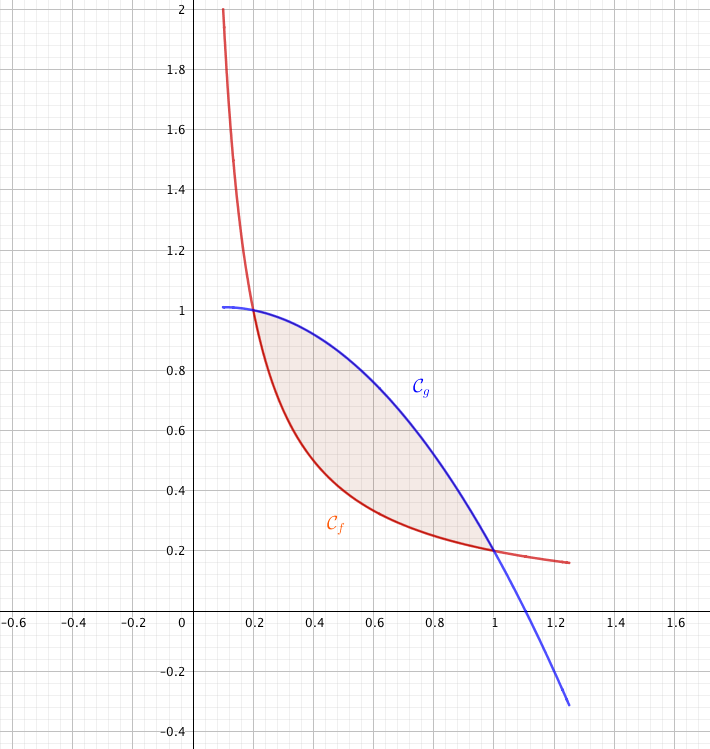

La feuille gauche du logo correspond à la partie grisée du plan, délimitée par ces deux courbes.

1. Vérifier par le calcul que 0,2 est une solution de l’équation $f(x) = g(x)$.
2. Déterminer graphiquement la seconde solution de cette équation.
3. 1. Interpréter graphiquement l’intégrale $I = \displaystyle\int_{0,2}^1 g(x) \text{d} x$.
   2. Donner une valeur approchée de cette intégrale à $10^{-2}$ près.
4. 1. Montrer que la fonction $F$ définie sur l’intervalle $[0,1; 1,25]$ par $F(x) = \frac{1}{5} \ln (x)$ est une primitive sur l’intervalle $[0,1; 1,25]$ de la fonction $f$.
   2. Calculer la valeur exacte de l’intégrale $J = \displaystyle\int_{0,2}^1 f(x) \text{d} x$.
5. On admet que la courbe $\mathcal{C}_g$ est située au-dessus de la courbe $\mathcal{C}_f$ sur l’intervalle $[0,2 ; 1]$.
   L’unité choisie sur chacun des axes est de 2,5 cm.
   En déduire, au cm$^2$ près, une valeur approchée de l’aire totale du logo.

Correction de l'exercice 2 (7 points)

Suites et fonctions

Suites et fonctions Les parties A et B de cet exercice sont indépendantes.
Le conservatoire des espaces naturels d'une région s’occupe d’une zone protégée de 1800 hectares. Depuis plusieurs années, il surveille le domaine d’extension d’une plante invasive. Cette plante inhabituelle, d’origine exotique, devient envahissante et cause une régression de la biodiversité. Si le conservatoire constate qu’à la fin d’une année l’aire de la surface occupée par la plante dépasse 80 hectares, cette plante fera alors l’objet d’un plan d’élimination progressive à partir de l’année suivante.

Partie A

1. Des relevés de la surface occupée par cette plante ont été effectués sur le terrain, en fin d'année, de 2015 à 2018 : $$\begin{array}{|c|c|c|c|c|} \hline \text{Année } & 2015 & 2016 & 2017& 2018 \\ \hline \text{Surface en hectares (ha) } &63 & 66,2 & 69,5&73 \\ \hline \end{array} $$ Le conservatoire estime que l’aire de la surface occupée par cette plante a augmenté de 5% environ chaque année.
   Vérifier que cette estimation est cohérente avec les relevés pris sur le terrain.
Pour augmenter de 5%, on multiplie par 1+5%= 1,05. On a ainsi :
• $63 \times 1,05= 66,15\approx 66,2$
• $66,2 \times 1,05= 69,51\approx 69,5$
• $69,5 \times 1,05= 72,975\approx 73$
Cette estimation est donc cohérente avec les relevés pris sur le terrain.
2. On considère qu’à partir de l’année 2018 la surface occupée par la plante augmente chaque année de 5%.
   Expliquer alors pourquoi la décision de commencer l'élimination de la plante devrait être prise à la fin de l'année 2020 par le conservatoire.
La surface occupée par la plante augmente chaque année de 5%.
• En 2018, la surface occupée est 73 ha.
• En 2019, la surface occupée est $73\times 1,05\approx 76,65$ ha
• En 2020, la surface occupée est $76,65\times 1,05\approx 80,5$ ha
La surface occupée par plante dépasse 80 hectares, cette plante fera alors l’objet d’un plan d’élimination progressive à partir de l’année suivante.
3. Le conservatoire décide de mettre en oeuvre un plan d’élimination progressive. Ce plan prévoit d’éliminer la plante, par arrachage ou par brûlage thermique, sur une surface de 10 hectares à chaque fin d’année, à partir de l’année 2021.
   Pour tout entier naturel $n$, on désigne par $P_n$ l’aire de la surface occupée par la plante, exprimée en hectares, en fin d’année « 2020 + $n$ », en prenant $P_0 = 80,5$.
   1. Montrer que $P_1 = 74,525$.
   $P_1 = 1,05P_0-10=74,525$ En effet, on passe de $P_0$ à $P_1$ en multipliant par 1,05( augmentation de 5%), puis on retranche 10, car on arrache ou on brûle , sur une surface de 10 hectares à chaque fin d’année.
   2. Justifier que pour tout entier naturel $n$, on a : $P_{n+1} = 1,05P_n - 10$.
   Comme $P_n$ est l’aire de la surface occupée par la plante, exprimée en hectares, en fin d’année « 2020 + $n$ », on a après augmentation de 5 % sur une année, il y aura $(1+0,05)P_n=1,05P_n$.
   Puis on brûle , sur une surface de 10 hectares à chaque fin d’année : $01,05P_n-10$
   D'où le résultat: $P_{n+1} = 1,05P_n - 10.$
   3. Donner une valeur arrondie de $P_2$ à $10^{-3}$ près.
   $$\begin{array}{rl} P_2&=1,05P_1-10 \\ & =1,05 \times74,525-10\\ &=68,25125 \end{array}$$ A $10^{-3}$ près $P_2\approx 68,251$
   4. Pourquoi la suite $\left (P_n\right )$ n’est-elle pas géométrique?
   Si la suite $\left (P_n\right )$ était géométrique de raison $q$ alors $P_1=qP_0$ et $P_2=qP_1$ .
   On doit avoir $\dfrac{P_1}{P_0}=\dfrac{P_2}{P_1}$
   Or $\dfrac{P_1}{P_0}=\dfrac{74,525}{80,5}\approx 0,926$ et $\dfrac{P_2}{P_1}=\dfrac{68,25125}{74,525}\approx 0,916$
   La suite $\left (P_n\right )$ n’est pas géométrique.
4. Le conservatoire décidera de mettre fin au plan d’élimination dès que l’aire de la surface occupée par la plante sera inférieure à 6 hectares. Recopier et compléter l’algorithme ci-contre pour qu'à la fin de son exécution, la variable $n$ contienne le nombre d’années de mise en oeuvre du plan. $$ \begin{array}{|l|}\hline N\gets 0\\ P \gets 80,5\\ \text{Tant que }\:P \geq 6\\ \hspace{0.8cm}U \gets \ldots\\ \hspace{0.8cm}N \gets \ldots~~~~~ \\ \text{Fin Tant que}\\ \hline \end{array} $$
$$ \begin{array}{|l|}\hline N\gets 0\\ P \gets 80,5\\ \text{Tant que }\:P \geq 6\\ \hspace{0.8cm}P \gets 1,05P-10\\ \hspace{0.8cm}N \gets N+1 \\ \text{Fin Tant que}\\ \hline \end{array} $$
5. À la fin de quelle année le plan d’élimination prendra-t-il fin?
Plusieurs méthodes sont possibles :
On saisit l'algorithme ci-dessus sur une calculatrice
On obtient $P_{10}\approx 5,35$
On peut également utiliser le mode suite de la calculatrice :
Le plan d’élimination prendra fin à la fin de l'année 2030.

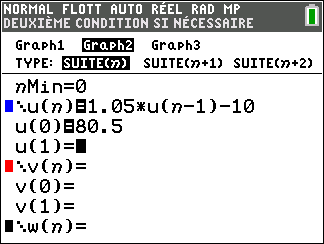
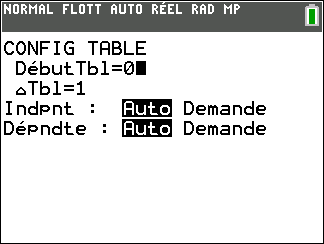
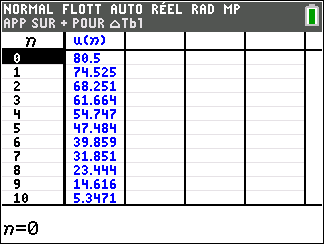
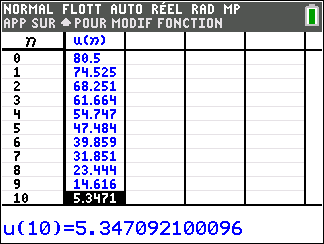
Partie B

Le logo utilisé par le conservatoire pour la communication est constitué de deux feuilles symétriques l’une de l’autre, dessinées ci-dessous. Soient les fonctions $f$ et $g$ définies sur l’intervalle $[0,1; 1,25]$ par $f(x) =\dfrac{0,2}{x}$ et $g(x) = -x^2 + 0,2x +1$. On note $\mathcal{C}_f$ et $\mathcal{C}_g$ les courbes représentatives de ces fonctions tracées dans le repère orthonormé ci-contre.

La feuille gauche du logo correspond à la partie grisée du plan, délimitée par ces deux courbes.

1. Vérifier par le calcul que 0,2 est une solution de l’équation $f(x) = g(x)$.
$f(0,2)=\dfrac{0,2}{0,2}=1$
$g(0,2) = -0,2^2 + 0,2\times 0,2 +1= -0,04+0,04+1=1$
0,2 est donc une solution de l’équation $f(x) = g(x)$.
2. Déterminer graphiquement la seconde solution de cette équation.
Graphiquement $A(1;1)$ est un point commun des courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ , donc 1 est donc une autre solution de l’équation $f(x) = g(x)$.
3. 1. Interpréter graphiquement l’intégrale $I = \displaystyle\int_{0,2}^1 g(x) \text{d} x$.
   La fonction $g$ est positive sur l’intervalle $[0,1; 1,25]$; en effet $\mathcal{C}_g$ est située au-dessus de laxe des abscisses sur l’intervalle $[0,1; 1,25]$.
   Donc l’intégrale $I = \displaystyle\int_{0,2}^1 g(x) \text{d} x$ représente l'aire, exprimée en unités d'aires, du domaine délimité par la courbe $\mathcal{C}_g$, l'axe des abscisses et les droites d'équations $x=0,2$ et $x=1$.
   2. Donner une valeur approchée de cette intégrale à $10^{-2}$ près.
   Ayant $g(x) = -x^2 + 0,2x +1$, on déduit $G$ une primitive de $g$: $$G(x)=-\dfrac{x^3}{3}+0,2\dfrac{x^2}{2}+x$$ $$\begin{array}{rlrl} I &= \displaystyle\int_{0,2}^1 g(x) \text{d} x &&\\ & =\left [ -\dfrac{x^3}{3}+0,2\dfrac{x^2}{2}+x \right ]_{0,2}^1&&\\ &&&\\ G(1)&= -\dfrac{1^3}{3}+0,2+0,2\dfrac{1^2}{2}+1& G(0,2)&=-\dfrac{0,2^3}{3}+0,2\dfrac{0,2^2}{2}+0,2\\ &=1,1-\dfrac{1}{3}&&\approx 0,7667\\ &\approx 0,2013&& \end{array}$$ $I = \displaystyle\int_{0,2}^1 g(x) \text{d} x=G(1)-G(0,2)\approx 0,57$
4. 1. Montrer que la fonction $F$ définie sur l’intervalle $[0,1; 1,25]$ par $F(x) = \frac{1}{5} \ln (x)$ est une primitive sur l’intervalle $[0,1; 1,25]$ de la fonction $f$.
   Il suffit de vérifier que la dérivée de$F$ est $f$.
   Comme $F(x) = \frac{1}{5} \ln (x)$, on déduit $F'(x)= \frac{1}{5}\times \frac{1}{x}=0,2\times \frac{1}{x}=\frac{0,2}{x}=f(x)$
   La fonction $F$ définie sur l’intervalle $[0,1; 1,25]$ par $F(x) = \frac{1}{5} \ln (x)$ est une primitive sur l’intervalle $[0,1; 1,25]$ de la fonction $f$.
   2. Calculer la valeur exacte de l’intégrale $J = \displaystyle\int_{0,2}^1 f(x) \text{d} x$.
$$\begin{array}{rlrl} J &= \displaystyle\int_{0,2}^1 f(x) \text{d} x&&\\ & =\left [ \frac{1}{5} \ln (x) \right ]_{0,2}^1&&\\ &&&\\ F(1)&= \frac{1}{5} \ln (1)& F(0,2)&=\frac{1}{5} \ln (0,2) \\ &=0&& = \frac{1}{5} \ln \left (\frac{1}{5}\right )\\ &&&=-\frac{\ln 5}{5} \\ && \end{array}$$ $$J = \displaystyle\int_{0,2}^1 f(x) \text{d} x =F(1)-F(0,2)= \frac{\ln 5}{5}$$
5. On admet que la courbe $\mathcal{C}_g$ est située au-dessus de la courbe $\mathcal{C}_f$ sur l’intervalle $[0,2 ; 1]$.
   L’unité choisie sur chacun des axes est de 2,5 cm.
   En déduire, au cm$^2$ près, une valeur approchée de l’aire totale du logo.
La courbe $\mathcal{C}_g$ est située au-dessus de la courbe $\mathcal{C}_f$ sur l’intervalle $[0,2 ; 1]$; l'aire du domaie délimité par les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ associée à l’intervalle $[0,2 ; 1]$ vaut, en unités d'aire : $$\begin{array}{rl} A&= \displaystyle\int_{0,2}^1 \left ( g(x)- f(x)\right ) \text{d} x \\ & = \displaystyle\int_{0,2}^1 \ g(x) \text{d} x - \displaystyle\int_{0,2}^1 \ f(x) \text{d} x \\ &= I-J\\ &\approx 0,57- \frac{\ln 5}{5}\\ &\approx 0,25\: \text{u.a.}\\ \end{array}$$ Ici l'unité d'aire vaut $2,5\times 2,5 =6,25$ cm$^2$ Donc l'aire du logo,cm$^2$ vaut $2A\approx 2\times 0,25\times 6,25\approx 3,125$ cm$^2$.
Au cm$^2$ près, l’aire totale du logo vaut environ 3 cm$^2$.

Exercice 3 4 points

Equations différentielles

Le clinker est un constituant du ciment qui résulte de la cuisson d’un mélange composé de calcaire et d’argile. La fabrication du clinker nécessite des fours à très haute température qui libèrent dans l’air une grande quantité de dioxyde de carbone (CO$_2$).
Dans une cimenterie, la fabrication du clinker s’effectue de 7h30 à 20h, dans une pièce de volume 900 000 dm$^3$.
À 20h, après une journée de travail, le taux volumique de CO$_2$ dans la pièce est de 0,6%.

1. Justifier que le volume de CO$_2$ présent dans cette pièce à 20h est de 5 400 dm$^3$.
2. Pour diminuer ce taux de CO$_2$ durant la nuit, l’entreprise a installé dans la pièce une colonne de ventilation. Le volume de CO$_2$, exprimé en dmdm$^3$, est alors modélisé par une fonction du temps $t$ écoulé après 20h, exprimé en minutes, $t$ varie ainsi dans l’intervalle [0; 690] puisqu'il y a 690 minutes entre 20h et 7h30. On admet que cette fonction $V$, définie et dérivable sur l’intervalle [0 ; 690] est une solution, sur cet intervalle, de l’équation différentielle (E) : $y' + 0,01y = 4,5$.
   1. Déterminer la solution générale de l’équation différentielle (E).
   2. Vérifier que pour tout réel $t$ de l’intervalle [0 ; 690], $V(t) =4950 \text{e}^{-0,01t} + 450$.
3. Quel sera, au dm$^3$ près, le volume de CO$_2$ dans cette pièce à 21h ?
4. Les responsables de la cimenterie affirment que chaque matin à 7h30 le taux de CO$_2$ dans cette pièce est inférieur à 0,06%.
   Cette affirmation est-elle vraie ? Justifier la réponse.
5. Déterminer l’heure à partir de laquelle le volume de CO$_2$ dans la pièce deviendra inférieur à 900 dm$^3$.

 

Correction de l'exercice 3 (5 points)

 

Equations différentielles

Le clinker est un constituant du ciment qui résulte de la cuisson d’un mélange composé de calcaire et d’argile. La fabrication du clinker nécessite des fours à très haute température qui libèrent dans l’air une grande quantité de dioxyde de carbone (CO$_2$).
Dans une cimenterie, la fabrication du clinker s’effectue de 7h30 à 20h, dans une pièce de volume 900 000 dm$^3$.
À 20h, après une journée de travail, le taux volumique de CO$_2$ dans la pièce est de 0,6%.

1. Justifier que le volume de CO$_2$ présent dans cette pièce à 20h est de 5 400 dm$^3$.
Le taux volumique de CO$_2$ dans la pièce est de 0,6% donc le volume de CO$_2$ présent dans cette pièce à 20h est de : $ 900 000 \times 0,006=5400$ dm$^3$.
2. Pour diminuer ce taux de CO$_2$ durant la nuit, l’entreprise a installé dans la pièce une colonne de ventilation. Le volume de CO$_2$, exprimé en dm$^3$, est alors modélisé par une fonction du temps $t$ écoulé après 20h, exprimé en minutes, $t$ varie ainsi dans l’intervalle [0; 690] puisqu'il y a 690 minutes entre 20h et 7h30. On admet que cette fonction $V$, définie et dérivable sur l’intervalle [0 ; 690] est une solution, sur cet intervalle, de l’équation différentielle (E) : $y' + 0,01y = 4,5$.
   1. Déterminer la solution générale de l’équation différentielle (E).
   L ’équation différentielle (E) : $y' + 0,01y = 4,5$ s'écrit $y'=-0,01y + 4,5$.
   Elle est donc du type $y'=ay+b$ où $a=-0,01$ et $b=4,5$.
   Les solutions sont les fonctions $y$ définies sur l’intervalle [0 ; 690] par $y==-\frac{b}{a}+K\text{a t}$, ici $-\frac{b}{a}=-\frac{4,5}{-0,01}=450$
   Lasolution générale de l’équation différentielle (E) est donc $y=K\text{e}^{-0,01t} + 450$ où $K$ désigne une constante réelle quelconque.
   2. Vérifier que pour tout réel $t$ de l’intervalle [0 ; 690], $V(t) =4950 \text{e}^{-0,01t} + 450$.
   A l'instant $t=0$, il est 20h et le volume de CO$_2$ présent dans cette pièce à 20h est de 5 400 dm$^3$; donc $V(0)=5400$ $$\begin{array}{rl} V(0)=5400& \iff K\text{e}^{-0,01\times 0} + 450 =5400\\ & \iff K\text{e}^{ 0} + 450 =5400\\ &\iff K + 450 =5400\\ &\iff K =4950\\ \end{array}$$ Donc pour tout réel $t$ de l’intervalle [0 ; 690], $V(t) =4950 \text{e}^{-0,01t} + 450$.
3. Quel sera, au dm$^3$ près, le volume de CO$_2$ dans cette pièce à 21h ?
Le volume de CO$_2$ dans cette pièce à 21h est $V(60)= 4950 \text{e}^{-0,01 \times 60} + 450\approx 3166,6$
A 21h, le volume de CO$_2$ dans cette pièce sera d'environ 3167 dm$^3$.
4. Les responsables de la cimenterie affirment que chaque matin à 7h30 le taux de CO$_2$ dans cette pièce est inférieur à 0,06%.
   Cette affirmation est-elle vraie ? Justifier la réponse.
à 7h30 le volume de CO$_2$ dans cette pièce est $V(690)= 4950 \text{e}^{-0,01 \times 60} + 450\approx 454,99$
Le taux de CO$_2$ dans cette pièce à 7h30 est environ $\dfrac{456}{900000}\approx 0,0005$.
Or $0,0005=0,05\%$.
L'affirmation est donc vraie.
5. Déterminer l’heure à partir de laquelle le volume de CO$_2$ dans la pièce deviendra inférieur à 900 dm$^3$.
On résout l'inéquation $V(t)<900$ : $$\begin{array}{rl} 4950 \text{e}^{-0,01t} + 450 <900 & \iff 4950 \text{e}^{-0,01t} < 450 \\ & \iff \text{e}^{-0,01t} < \frac{450}{4950} \\ &\iff \text{e}^{-0,01t} < \frac{1}{11} \\ &\iff \ln\left ( \text{e}^{-0,01t}\right ) < \ln\left ( \frac{1}{11}\right ) \\ &\iff -0,01t < \ln\left ( \frac{1}{11}\right ) \\ &\iff t > \frac{\ln\left ( \frac{1}{11}\right ) }{-0,01}\\ & \iff t > -100 \times \left (-\ln (11)\right )\\ &\iff t > 100 \ln (11) \end{array}$$ $100 \ln (11) \approx 239,79$, or $240$ min=4h.
A minuit, le volume de CO$_2$ dans la pièce deviendra inférieur à 900 dm$^3$.

 

Exercice 4 5 points

Probabilités

Dans cet exercice, les résultats sont à arrondir à 10$^{-3}$ près.
Les trois parties sont indépendantes.

Partie A

Les téléphones portables intègrent des capteurs photographiques de plus en plus évolués. Ces capteurs sont fragiles et ont une durée de vie limitée. La durée de fonctionnement sans panne, exprimée en années, d’un capteur photographique est modélisée par une variable aléatoire $D$ qui suit la loi normale de paramètres $\mu = 4$ et $\sigma = 1,23$.

1. Quelle est la durée moyenne de fonctionnement sans panne d’un capteur photographique?
2. Déterminer la probabilité $P (3,5 \leq D \leq 4,5)$.
3. Lors de l’achat d’un téléphone portable, la garantie pièces et main d’oeuvre est de deux ans. Quelle est la probabilité que la durée de fonctionnement sans panne d’un capteur photographique soit inférieure à la durée de garantie ?

Partie B

Lorsqu’un téléphone portable devient défectueux et qu’il est encore sous garantie, le client peut le déposer dans un point de vente agréé pour réparation ou échange contre un appareil neuf.
On s'intéresse au temps d’attente, exprimé en jours, avant le retour de l’appareil, réparé ou échangé. Ce temps peut être modélisé par une variable aléatoire T qui suit la loi exponentielle de paramètre $\lambda = 0,025$.

1. 1. Déterminer l’espérance $E(T)$ de la variable aléatoire $T$.
   2. nterpréter cette valeur dans le contexte.
2. Un téléphone portable, défectueux et encore sous garantie, a été déposé par un client dans un point de vente agréé.
   1. Calculer la probabilité $P (T \leq 7)$ et interpréter ce résultat.
   2. Calculer la probabilité que le client doive attendre plus de 20 jours avant de récupérer son téléphone portable.

Partie C

Un magazine spécialisé souhaite comparer l’efficacité des services après-vente (SA.V) pour les téléphones portables de deux marques A et B. Après une enquête auprès de clients, le magazine obtient les résultats suivants : $$\begin{array}{|c|c|c|} \hline \text{Marque de téléphone}& \text{Nombre de clients du S.A.V ayant répondu à l’enquête}& \text{Nombre de clients indiquant avoir récupéré leur téléphone en moins de 20 jours} \\ \hline A& 120 & 47 \\ \hline B& 92 & 26 \\ \hline \end{array} $$

1. 1. On admet que l’intervalle de confiance, au niveau de confiance 95%, de la proportion de clients ayant récupéré en moins de 20 jours leur téléphone de marque A est [0,304; 0,480].
   Déterminer l’intervalle de confiance, au niveau de confiance 95%, de la proportion de clients ayant récupéré en moins de 20 jours leur téléphone de marque B.
2. Au vu des deux intervalles de confiance obtenus, le magazine peut-il indiquer à ses lecteurs qu'il y a une différence significative dans l’efficacité des deux S.A.V ? Justifier la réponse.

 

Exercice 4 5 points

Probabilités

Dans cet exercice, les résultats sont à arrondir à 10$^{-3}$ près.
Les trois parties sont indépendantes.

Partie A

Les téléphones portables intègrent des capteurs photographiques de plus en plus évolués. Ces capteurs sont fragiles et ont une durée de vie limitée. La durée de fonctionnement sans panne, exprimée en années, d’un capteur photographique est modélisée par une variable aléatoire $D$ qui suit la loi normale de paramètres $\mu = 4$ et $\sigma = 1,23$.

1. Quelle est la durée moyenne de fonctionnement sans panne d’un capteur photographique?
La durée moyenne de fonctionnement sans panne d’un capteur photographique est donnée par $E(D)=\mu= 4$ années.
2. Déterminer la probabilité $P (3,5 \leq D \leq 4,5)$.

2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

 

La probabilité pour que le capteur photographique fonctionne sans panne entre 3 ans 6 mois et 4ans 6 mois vaut environ 0,316.
3. Lors de l’achat d’un téléphone portable, la garantie pièces et main d’oeuvre est de deux ans. Quelle est la probabilité que la durée de fonctionnement sans panne d’un capteur photographique soit inférieure à la durée de garantie ?
On calcule $P(D<2)$ :

2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$

$$P( \5 \leq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$

Partie B

Lorsqu’un téléphone portable devient défectueux et qu’il est encore sous garantie, le client peut le déposer dans un point de vente agréé pour réparation ou échange contre un appareil neuf.
On s'intéresse au temps d’attente, exprimé en jours, avant le retour de l’appareil, réparé ou échangé. Ce temps peut être modélisé par une variable aléatoire T qui suit la loi exponentielle de paramètre $\lambda = 0,025$.

1. 1. Déterminer l’espérance $E(T)$ de la variable aléatoire $T$.
   L’espérance de la variable aléatoire $T$ est $E(T)=\dfrac{1}{\lambda}=\dfrac{1}{0,025}=40$.
   
   2. nterpréter cette valeur dans le contexte.
   Le temps d'attente moyen avant le retour de l’appareil, réparé ou échangé est de 40 jours.
2. Un téléphone portable, défectueux et encore sous garantie, a été déposé par un client dans un point de vente agréé.
   1. Calculer la probabilité $P (T \leq 7)$ et interpréter ce résultat.
   La densité de probabilité de $T$ est $f(t)=\lambda \text{e}^{-\lambda .t}$. Donc : $$\begin{array}{rl} P (T \leq 7)&= \displaystyle\int_0^7 \lambda \text{e}^{-\lambda .t}\text{d}t \\ & =\left [ - \text{e}^{-\lambda .t} \right ] _0^7\\ & =- \text{e}^{-7\lambda }-\left (- \text{e}^{0}\right )\\ &=1- \text{e}^{-7\times 0,025 } \\ &\approx 0,161 \\ \end{array}$$ $P(T\leq 7)\approx 0,161$.
   La probabilité pour que ce client attende moins de 7 jours avant le retour de l’appareil, réparé ou échangé vaut environ 0,161.
   2. Calculer la probabilité que le client doive attendre plus de 20 jours avant de récupérer son téléphone portable.
   On calcule ici $P(T\geq 20)$ : $$\begin{array}{rl} P (T \geq 20)&=1-P(T<20)\\ &=1- \displaystyle\int_0^{20} \lambda \text{e}^{-\lambda .t}\text{d}t \\ & =1-\left [ - \text{e}^{-\lambda .t} \right ] _0^{20}\\ & =1-\left ( 1- \text{e}^{-20\lambda } \right )\\ &= \text{e}^{-20\times 0,025 } \\ &\approx 0,607 \\ \end{array}$$ Il y a environ 60,7% de chances que ce client attende plus de 20 jours avant de récupérer son téléphone portable.

Partie C

Un magazine spécialisé souhaite comparer l’efficacité des services après-vente (SA.V) pour les téléphones portables de deux marques A et B. Après une enquête auprès de clients, le magazine obtient les résultats suivants : $$\begin{array}{|c|c|c|} \hline \text{Marque de téléphone}& \text{Nombre de clients du S.A.V ayant répondu à l’enquête}& \text{Nombre de clients indiquant avoir récupéré leur téléphone en moins de 20 jours} \\ \hline A& 120 & 47 \\ \hline B& 92 & 26 \\ \hline \end{array} $$

1. 1. On admet que l’intervalle de confiance, au niveau de confiance 95%, de la proportion de clients ayant récupéré en moins de 20 jours leur téléphone de marque A est [0,304; 0,480].
   Déterminer l’intervalle de confiance, au niveau de confiance 95%, de la proportion de clients ayant récupéré en moins de 20 jours leur téléphone de marque B.

La fréquence est égale à  $\1$. La taille $n$ de l'échantillon considéré est égale à  $\2.$
Comme  $ n =\2$ ,   $n \times \8  $=\3  et $n\times (1-\8)=\4,$ les conditions d'utilisation d'un intervalle de confiance sont réunies.

En effet on a bien : $$n \geq 30\;;\; n \times \8 \geq 5 \text{ et } n\times (1-\8) \geq 5$$

L' intervalle de confiance avec un niveau de confiance de 95% est : \[\9 = \left[\8 - 1,96\sqrt{\dfrac{\8(1 - \8)}{n}}~;~\8 + 1,96\sqrt{\dfrac{\8(1 - \8)}{n}} \right]\]
La fréquence est $\8=\1$.
L'intervalle de confiance au niveau de 95% est \[\9 = \left[\1 - 1,96\sqrt{\dfrac{\1 (1 - \1 )}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1 (1 - \1 )}{\2}} \right]\approx[\5~;~\6]\] 

2. Au vu des deux intervalles de confiance obtenus, le magazine peut-il indiquer à ses lecteurs qu'il y a une différence significative dans l’efficacité des deux S.A.V ? Justifier la réponse.
On a $IC_A\approx [0,304; 0,480]$ et $IC_B\approx [0,190; 0,375]$.
Les deux intervalles de confiance ne sont pas disjoints. Il n'y a donc pas de différence significative dans l’efficacité des deux S.A.V.