Baccalauréat S Nouvelle-Calédonie mars 2016 - Correction Exercice 2
Correction de l'exercice 2 (3 points)
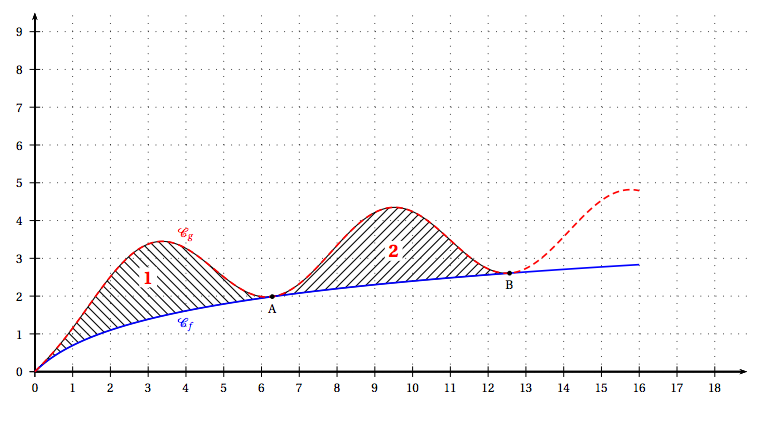
$f$ et $g$ sont deux fonctions continues sur $[0;16]$ en tant que composée et somme de fonction continues sur cet intervalle.
Pour tout réel $x$, $1-\cos x \ge 0$ donc $f(x) \le g(x)$. et $f(x)=g(x) \Leftrightarrow x=2k\pi $ où $k\in \mathbb Z$.
Par conséquent l’abscisse de $A$ est $2\pi$ et celle de $B$ est $4\pi$.
Il s’agit alors de calculer l’aire du domaine compris entre $\mathscr{C}_g$ et $\mathscr{C}_g$ et les droites d’équations $x=0$ et $x=2\pi$ dans un premier temps et $x=2\pi$^et $x=4\pi$.
On veut donc comparer $\displaystyle I=\int_0^{2\pi} \left(g(x)-f(x)\right)\mathrm{d}x$ et $\displaystyle I=\int_{2\pi}^{4\pi} \left(g(x)-f(x)\right)\mathrm{d}x$.
Or $g(x)-f(x)=1-\cos x$.
Donc
$\begin{align*} I&=\int_0^{2\pi} \left(1-\cos x\right)\mathrm{d}x \\
&=\left[x-\sin x\right]_0^{2\pi} \\
&= 2\pi
\end{align*}$
$\begin{align*} J&=\int_{2\pi}^{4\pi} \left(1-\cos x\right)\mathrm{d}x \\
&=\left[x-\sin x\right]_{2\pi}^{4\pi} \\
&= 4\pi-2\pi \\
&=2\pi
\end{align*}$
$\quad$
En vidéo !
- Vues: 36534
