Rédigé par Luc Giraud le 19 juillet 2019. Publié dans Annales STI2D 2019.

Baccalauréat STI2D Antilles-Guyane - 19 juin 2019 - Correction Exercice 1

Page 2 sur 8: Correction Exercice 1

Page 2 sur 8

Correction de l'exercice 1 (4 points)

QCM

Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse ne rapportent ni n'enlèvent aucun point.

Indiquer sur la copie le numéro de la question et la réponse correspondante choisie.

$\ln$ désigne la fonction logarithme népérien.
$\mathrm{i}$ désigne le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$

Pour tout réel a strictement positif, ln(2a)+ln(8a)2 est égal à :
1. $\ln(4a)$
2. $\ln(5a)$
3. $\ln(16a)$
4. $\ln\left(8a^2\right)$

$a$

$\begin{array}{rcl} \frac{\ln (2 a) + \ln (8 a)}{2} & = & \frac{\ln (2 a \times 8 a)}{2} \\ = & \frac{\ln (16 a^{2})}{2} \\ = & \ln (\sqrt{16 a^{2}}) \\ = & \ln (4 a) \end{array}$

On considère une fonction f définie et dérivable sur ]0;+∞[. On appelle C sa courbe représentative dans un repère orthonormé (O, →i, →j). On admet que limx→0f(x)=−∞ et que limx→+∞f(x)=+∞. La courbe C admet :
1. deux asymptotes parallèles à l'axe des ordonnées
2. une asymptote parallèle à l'axe des ordonnées et une asymptote parallèle à l'axe des abscisses
3. une asymptote parallèle à l'axe des ordonnées et aucune asymptote parallèle à l'axe des abscisses
4. deux asymptotes parallèles à l'axe des abscisses

$\displaystyle{\lim_{x \to 0}}f(x)=-\infty$

$\mathcal{C}$

$x=0$

$\displaystyle{\lim_{x \to +\infty}}f(x)=+\infty$

$\mathcal{C}$

On considère le nombre complexe z=−2eiπ4. Soit ¯z le nombre complexe conjugué de z. Une écriture exponentielle de ¯z est :
1. $2\text{e}^{\mathrm{i}\frac{\pi}{4}}$
2. $2\text{e}^{-\mathrm{i}\frac{\pi}{4}}$
3. $2\text{e}^{-\mathrm{i}\frac{5\pi}{4}}$
4. $2\text{e}^{\mathrm{i}\frac{5\pi}{4}}$

$z = - 2 e^{i \frac{π}{4}} = - 1 \times 2 e^{i \frac{π}{4}} = 2 \times e^{i π} \times e^{i \frac{π}{4}} = 2 e^{i \frac{5 π}{4}}$

$\bar{z} = 2 e^{- i \frac{5 π}{4}}$

Le plan complexe est muni d'un repère orthonormé (O;→u,→v). Les droites d'équation y=x et y=−x partagent le plan en quatre zones ①, ②, ③ et ④ comme indiqué ci-dessous :

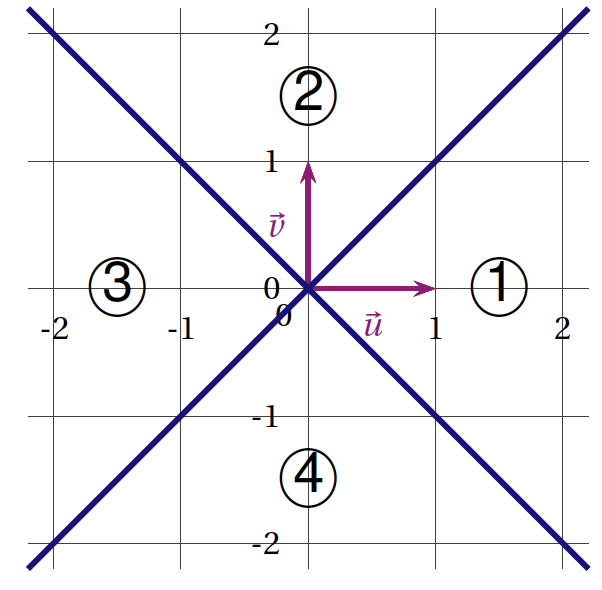
Soit z un nombre complexe non nul. On sait que :
- la partie réelle de z est strictement inférieure à sa partie imaginaire ;
-un argument de z est strictement compris entre 3π4 et 2π.
Le point image de z se situe :
1. dans la zone ①
2. dans la zone ②
3. dans la zone ③
4. dans la zone ④

La condition « la partie réelle de $z$ est strictement inférieure à sa partie imaginaire » permet d'éliminer la partie du plan grisée.
La condition « un argument de z est strictement compris entre $\dfrac{3\pi}{4}$ et $2\pi$ » permet d'éliminer la partie du plan hachurée.

QCM4

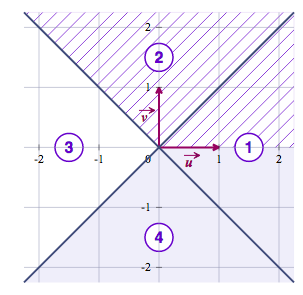
Le point image de z se situe donc dans la zone ③

Vues: 18862

Imprimer

Baccalauréat STI2D Antilles-Guyane - 19 juin 2019 - Correction Exercice 1

Correction de l'exercice 1 (4 points)

Rechercher