Bac STI2D Métropole 16 juin 2016 - Exercice 4

Page 7 sur 8: Exercice 4

Exercice 4 6 points

Probabilités

Les parties A et B sont indépendantes.
Un pont levant enjambant un canal peu fréquenté est constitué d'un tablier qui, une fois relevé, permet le passage de bateaux de différentes tailles.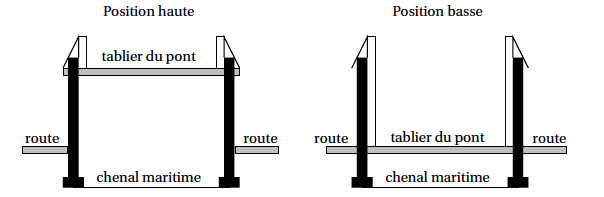

$$\begin{array}{|l |} \hline \text{Hauteur du tablier en position haute : 7 mètres}\\ \text{Longueur du tablier : 30 mètres}\\ \text{Temps de montée du tablier : 2 minutes}\\ \text{Temps en position haute du tablier (hors incident) : 8 minutes}\\ \text{Temps de descente du tablier : 2 minutes}\\ \hline \end{array} $$

Partie A - Sur la route

Un automobiliste se présente devant le pont. Le tablier du pont est en position haute. On s'intéresse ici au temps d'attente D, exprimé en minutes, de l'automobiliste avant qu'il puisse franchir le canal, pont baissé (hors incident).

 

1. Combien de temps l'automobiliste attend-il au minimum ? au maximum?
2. On admet que le temps d'attente, en minutes, de l'automobiliste pour franchir le pont est une variable aléatoire D qui suit la loi uniforme sur l'intervalle [2 ;10].
   Déterminer l'espérance E(D) de la variable aléatoire D et interpréter le résultat dans le contexte.
3. Calculer la probabilité que le temps d'attente de l'automobiliste ne dépasse pas 5 minutes.

Partie B - Sur l'eau

Dans cette partie les résultats demandés seront arrondis à $10^ {-2}$ près.
Lorsqu'un bateau est passé, le tablier du pont revient en position basse. Le temps, exprimé en heures, avant que le bateau suivant se présente devant le pont est une variable aléatoire T qui suit la loi exponentielle de paramètre $\lambda = 0,05$. Ce temps est appelé temps de latence.

1. Déterminer l'espérance E(T) de la variable aléatoire T et interpréter le résultat dans le contexte.
2. On considère la fonction $f$ définie sur $[0 , +\infty[$ par $f (x) = 0,05 \text{e}^{-0,05 x}$.
   1. Montrer que la fonction $F$ définie sur$[0 , +\infty[$ par $F(x) =-\text{e}^{-0,05 x}$ est une primitive de $ f$ .
   2. On rappelle que pour tout nombre réel $t$ de $[0 , +\infty[ , P(T \leq t) = \displaystyle\int_0 ^t f(x)\; dx$.
      Démontrer que $P(T \leq t) =1- \text{e}^{-0,05 t}$.
3. 1. Calculer la probabilité que le temps de latence soit inférieur à une demi-journée, soit 12 heures.
   2. Calculer la probabilité que le temps de latence soit supérieur à un jour.
   3. Calculer $P(12\leq T\leq 24)$.