Bac STI2D Nouvelle-Calédonie 15 novembre 2016
Exercice 1 5 points
- La politique communautaire de gestion des déchets et ses déclinaisons françaises sont définies par de nombreuses directives, dont la portée varie. Certaines ont une portée générale et d'autres concernent certaines catégories de déchets spécifiques.
- Le Projet de Plan national de prévention des déchets $2010-2020$ concerne les déchets ménagers et assimilés (DMA). L'objectif proposé par ce projet est une réduction annuelle de 7 % des DMA produits par habitant entre $2010$ et $2020$.
- Les DMA produits en France ont été de $590$ kg par habitant en $2011$ et de $570$ kg par habitant en $2013$.
Source ADEME
Partie A :
La réduction des DMA produits entre 2011 et 2013 atteint-elle l'objectif fixé par le Projet de Plan national de prévention des déchets ?
Partie B :
On considère que les objectifs du plan national de prévention des déchets sont atteints à partir de 2013. On modélise par une suite $\left(u_n\right)$ la quantité de DMA produits en kg par habitant, le terme $u_n$ correspondant à l'année $(2013 + n)$. Ainsi $u_0 = 570$.
- Calculer $u_1$.
- Quelle est la quantité de DMA produits, arrondie au kg par habitant, en 2015 ?
- Déterminer la nature de la suite $\left(u_n\right)$ puis exprimer $u_n$ en fonction de $n$.
PartieC :
On considère l'algorithme ci-dessous : $$\begin{array}{|ll|}\hline \text{Variables } &\\ &n : \text{ un nombre entier naturel}\\ &q : \text{ un nombre réel }\\ &U : \text{ un nombre réel }\\ \text{Entrée} &\\ &\text{ Saisir }n\\ \text{ Initialisation } &\\ &\text{ Affecter à } u \text{ la valeur }570\\ &\text{ Affecter à } q \text{la valeur } 0,93\\ \text{ Traitement } &\\ &\text{ Répéter } n \text{ fois } \\ &\hspace{0.5cm} \text{ Affecter à } u \text{ la valeur } u \times q\\ \text{Sortie } &\\ &\text{ Afficher } u\\ \hline \end{array}$$
- On entre dans l'algorithme la valeur $n = 4$. Faire fonctionner cet algorithme pour compléter les cases non grisées du tableau suivant, que l'on recopiera (on donnera des valeurs arrondies au kg près par habitant). $$ \begin{array}{ |c|c|c|c| }\hline & n & q & u \\ \hline \text{ Entrées et initialisation }& 4 &0,93 &570\\ \hline 1 er \text{ passage dans la boucle de l'algorithme }&&&\\ \hline 2 e \text{ passage dans la boucle de l'algorithme} &&&\\ \hline 3 e \text{ passage dans la boucle de l'algorithme} &&&\\ \hline 4 e \text{ passage dans la boucle de l'algorithme} &&&\\ \hline \end{array} $$
- Interpréter la valeur de $u$ obtenue au quatrième passage dans la boucle de l'algorithme.
- Quel sera le pourcentage de réduction des DMA produits entre 2013 et 2017 si l'objectif du Projet de Plan national de prévention des déchets est atteint chaque année?
- Quelle devrait être la quantité de DMA produits en 2020 pour atteindre l'objectif fixé par le Projet de Plan national de prévention des déchets?
Correction de l'exercice 1 (5 points)
- La politique communautaire de gestion des déchets et ses déclinaisons françaises sont définies par de nombreuses directives, dont la portée varie. Certaines ont une portée générale et d'autres concernent certaines catégories de déchets spécifiques.
- Le Projet de Plan national de prévention des déchets $2010-2020$ concerne les déchets ménagers et assimilés (DMA). L'objectif proposé par ce projet est une réduction annuelle de 7 % des DMA produits par habitant entre $2010$ et $2020$.
- Les DMA produits en France ont été de $590$ kg par habitant en $2011$ et de $570$ kg par habitant en $2013$.
Source ADEME
Partie A :
La réduction des DMA produits entre 2011 et 2013 atteint-elle l'objectif fixé par le Projet de Plan national de prévention des déchets ?
- méthode 1: Le coefficient multiplicateur associé à une baisse de 7 % est $1-\frac{7}{100}=0,93$.
Avec une réduction annuelle de 7 % des DMA, la quantité de DMA par habitant en 2013 devrait être de : $590\times 0,932=510,291$
Les DMA produits en France ayant été de 570 kg par habitant en 2013, l'objectif fixé par le Projet de Plan national de prévention des déchets n'est pas atteint en 2013. - méthode 2 : Calculons le pourcentage d'évolution annuel moyen des DMA produits en France entre 2011 et 2013 :
$590\times (1+\frac{t}{100})^2=570\iff 1+\frac{t}{100} =\left(\frac{570}{590}\right)^\frac{1}{2}\iff t≈-1,7$
Avec une réduction annuelle d'environ 1,7 % des DMA produits par habitant entre 2011 et 2013, l'objectif fixé par le Projet de Plan national de prévention des déchets n'est pas atteint en 2013.
Partie B :
On considère que les objectifs du plan national de prévention des déchets sont atteints à partir de 2013. On modélise par une suite $\left(u_n\right)$ la quantité de DMA produits en kg par habitant, le terme $u_n$ correspondant à l'année $(2013 + n)$. Ainsi $u_0 = 570$.
- Calculer $u_1$. $u_1= 570\times \left(1-\frac{7}{100}\right)= 510,291$
- Quelle est la quantité de DMA produits, arrondie au kg par habitant, en 2015 ? $u_2=530,1\times 0,93=492,993$
- Déterminer la nature de la suite $\left(u_n\right)$ puis exprimer $u_n$ en fonction de $n$. Pour tout entier $n$ on a $u_{n+1}=0,93\times u_n$
$u1=530,1.$
Les DMA produits en France ont été d'environ 493 kg par habitant en 2015.
donc $(u_n)$ est une suite géométrique de raison $q=0,93$.
$(u_n)$ est une suite géométrique de raison $q=0,93$ et de premier terme $u_0=570$
donc pour tout entier $n$ on a $u_n=570\times 0,93^n$.
PartieC :
On considère l'algorithme ci-dessous : $$\begin{array}{|ll|}\hline \text{Variables } &\\ &n : \text{ un nombre entier naturel}\\ &q : \text{ un nombre réel }\\ &U : \text{ un nombre réel }\\ \text{Entrée} &\\ &\text{ Saisir }n\\ \text{ Initialisation } &\\ &\text{ Affecter à } u \text{ la valeur }570\\ &\text{ Affecter à } q \text{la valeur } 0,93\\ \text{ Traitement } &\\ &\text{ Répéter } n \text{ fois } \\ &\hspace{0.5cm} \text{ Affecter à } u \text{ la valeur } u \times q\\ \text{Sortie } &\\ &\text{ Afficher } u\\ \hline \end{array}$$
- On entre dans l'algorithme la valeur $n = 4$. Faire fonctionner cet algorithme pour compléter les cases non grisées du tableau suivant, que l'on recopiera (on donnera des valeurs arrondies au kg près par habitant). $$ \begin{array}{ |c|c|c|c| }\hline & n & q & u \\ \hline \text{ Entrées et initialisation }& 4 &0,93 &570\\ \hline 1 er \text{ passage dans la boucle de l'algorithme }&&& 530\\ \hline 2 e \text{ passage dans la boucle de l'algorithme} &&& 493\\ \hline 3 e \text{ passage dans la boucle de l'algorithme} &&&458\\ \hline 4 e \text{ passage dans la boucle de l'algorithme} &&& 426\\ \hline \end{array} $$
- Interpréter la valeur de $u$ obtenue au quatrième passage dans la boucle de l'algorithme. La quantité de DMA produits en 2017 devrait être d'environ 426 kg par habitant.
- Quel sera le pourcentage de réduction des DMA produits entre 2013 et 2017 si l'objectif du Projet de Plan national de prévention des déchets est atteint chaque année? $0,93^4\approx 0,748$ ce qui correspond à une réduction d'environ 25,2 %.( 1-0,748= 0,252)
- Quelle devrait être la quantité de DMA produits en 2020 pour atteindre l'objectif fixé par le Projet de Plan national de prévention des déchets? $u_7=570\times 0,93^7\approx 343$ La quantité de DMA produits en 2020 devrait être d'environ 343 kg par habitant.
Exercice 2 5 points
Pour chacune des cinq affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée.
Une réponse non justifiée n'est pas prise en compte.
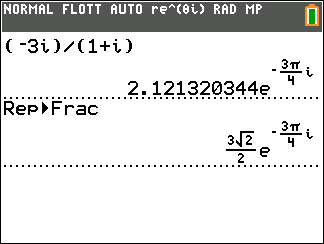
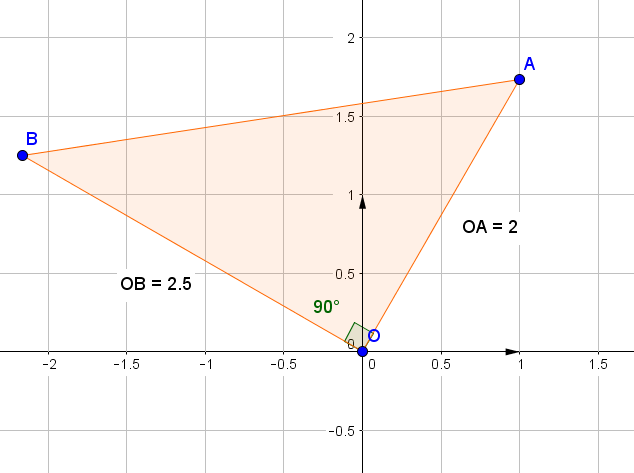
- Considérons les deux nombres complexes $z_1 = \sqrt{2}\text{e}^{\text{i}\frac{3\pi}{4}}$ et $z_2 = 1 - \text{i}\sqrt{3}$ où i est le nombre complexe de module 1 et d'argument $\frac{\pi}{2}$.
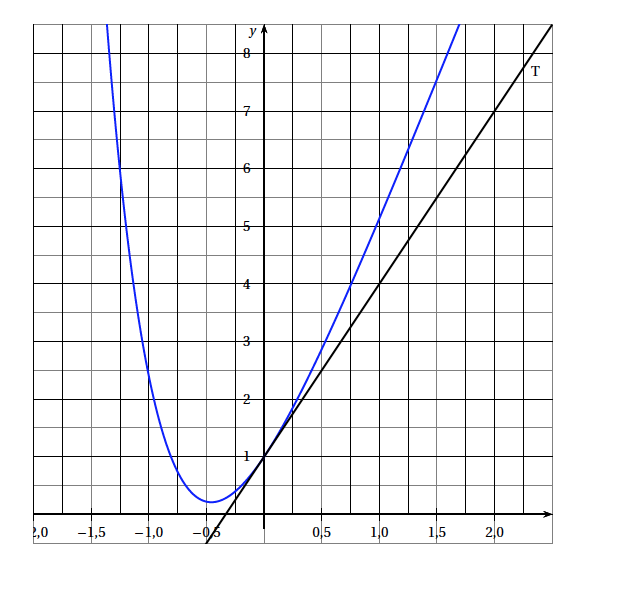
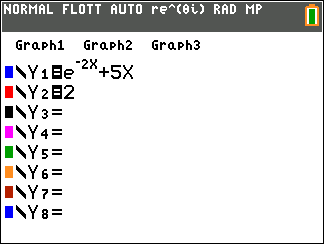
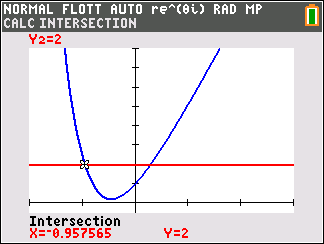
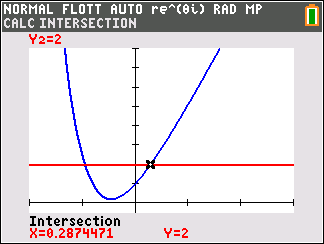
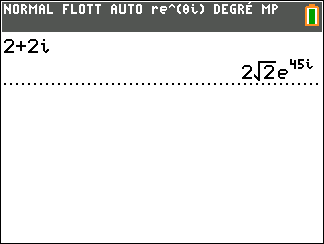
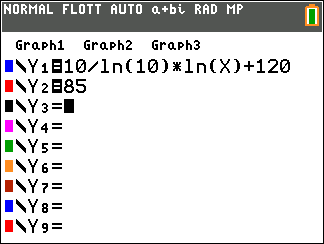
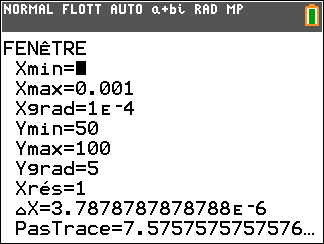
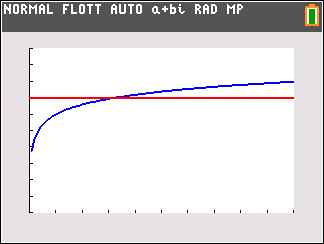
Affirmation 1 : Le produit $z_1 \times z_2$ est égal à $2\sqrt{2}\text{e}^{\text{i}\frac{5\pi}{12}}$. - Affirmation 2 : La solution $f$ de l'équation différentielle $y" + 4y = 0$ qui vérifie $f(0) = - 1$ et $f'(0) = 2$ admet comme représentation graphique :
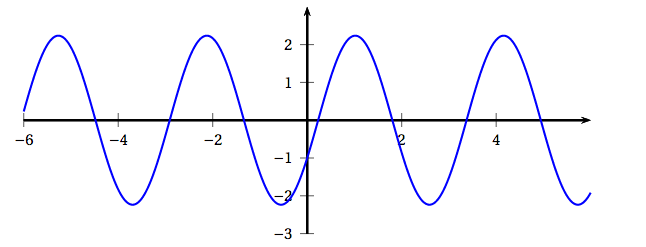
- Affirmation 3 : La solution de l'équation $\ln(x + 3) = 5$ est $\text{e}^5 - 3$.
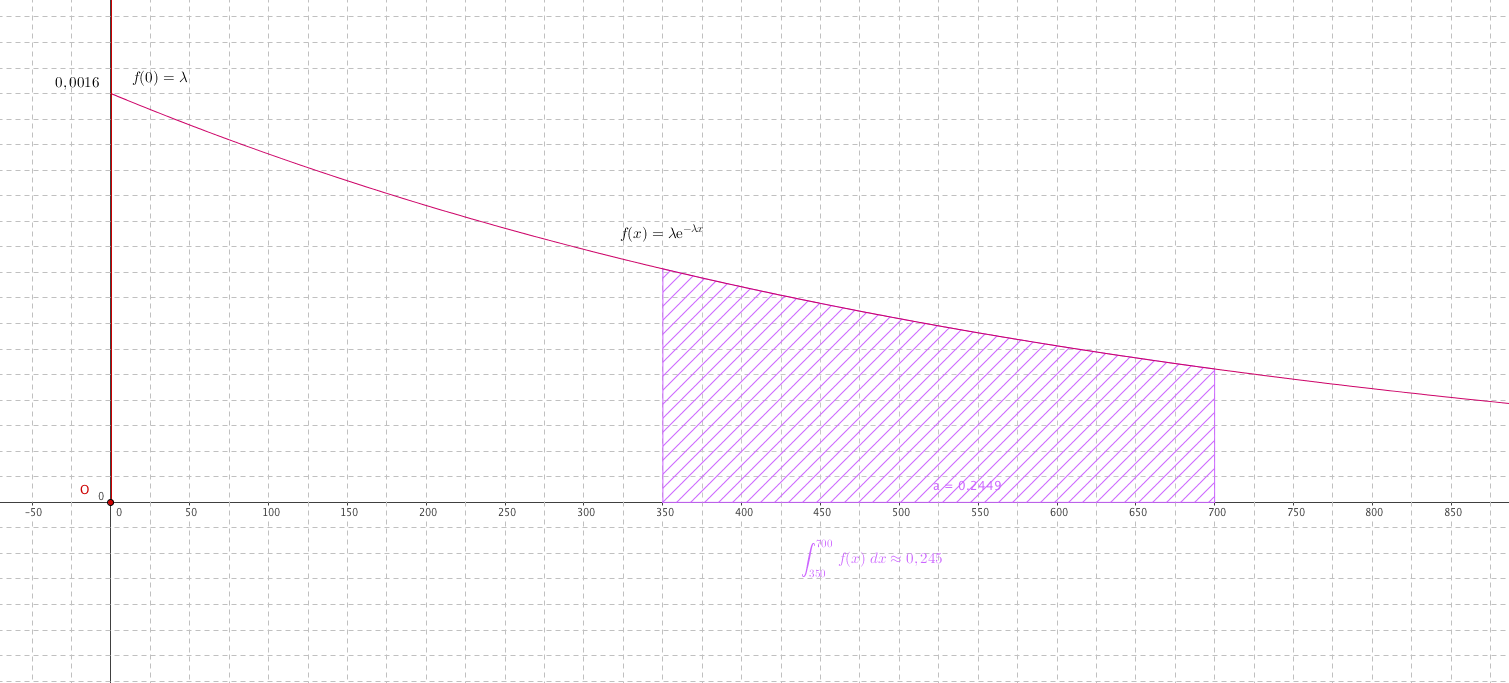
- La durée de vie en heures d'un certain type d'ampoules électriques est modélisée par une variable aléatoire qui suit la loi exponentielle de paramètre $\lambda = 0,000125 \: \left(\text{exprimé en } \:h\right)$.
Affirmation 4 : En moyenne, la durée de vie d'une ampoule est 1250 h. - Affirmation 5 : la fonction $F(x) = x\ln x - x + 2$ est une primitive de la fonction $f(x) = \ln x$ sur l'intervalle $]0~;~+\infty[$.
Correction de l'exercice 2 (5 points)
Pour chacune des cinq affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée.
Une réponse non justifiée n'est pas prise en compte.
- Considérons les deux nombres complexes $z_1 = \sqrt{2}\text{e}^{\text{i}\frac{3\pi}{4}}$ et $z_2 = 1 - \text{i}\sqrt{3}$ où i est le nombre complexe de module 1 et d'argument $\frac{\pi}{2}$.
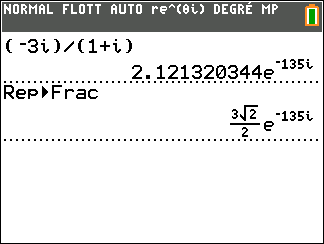
Affirmation 1 : Le produit $z_1 \times z_2$ est égal à $2\sqrt{2}\text{e}^{\text{i}\frac{5\pi}{12}}$. Déterminons la forme exponentielle du nombre complexe $z_2=1-\text{i}\sqrt 3$ : $$\begin{array}{cc} \text{ Module} & \text{ Argument} \\ \begin{array}{rl|rl} |z |&=\sqrt{a^2+b^2} \\ & =\sqrt{ 1^2+\sqrt{3}^2}\\ &=\sqrt 4\\ &= 2 \end{array}& \left\lbrace \begin{array}{l} \cos \theta=\frac{a}{r}~=\frac{1}{2}\\ ~\sin \theta=\frac{b}{r}~=-\frac{\sqrt 3}{2} \end{array} \right.\\ &\text{ Donc } \theta = - \frac{\pi}{3} \text{ convient } \end{array}$$ $$z= 1 - \text{i}\sqrt 3= 2\left(\cos\left(-\frac{\pi}{3} \right) +\text{i}\sin \left(-\frac{\pi}{3} \right) \right)= 2 \text{e}^{-\text{i}\frac{\pi}{3}}$$ $$\begin{array}{rl} z_1\times z_2 &= \sqrt{2}\text{e}^{\text{i}\frac{3\pi}{4}} \times 2 \text{e}^{-\text{i}\frac{\pi}{3}} \\ & =\sqrt{2}\text{e}^{\text{i}\frac{9\pi}{12}}\times 2 \text{e}^{-\text{i}\frac{4\pi}{12}} \\ &= 2\sqrt{2}\text{e}^{\text{i}\frac{5\pi}{12}} \end{array}$$ $$\text{Le produit } z_1 \times z_2 \text{ est égal à } 2\sqrt{2}\text{e}^{\text{i}\frac{5\pi}{12}}$$ - Affirmation 2 : La solution $f$ de l'équation différentielle $y" + 4y = 0$ qui vérifie $f(0) = - 1$ et $f'(0) = 2$ admet comme représentation graphique :
 Les solutions de l'équation différentielle $y"+4 y=0$ ( du type $y"+\omega ^2 y=0$ avec $\omega =2$ sont les fonctions $f$ de la forme $f:x\mapsto A\cos \left(2x \right)+B\sin \left(2 x \right)$
Les solutions de l'équation différentielle $y"+4 y=0$ ( du type $y"+\omega ^2 y=0$ avec $\omega =2$ sont les fonctions $f$ de la forme $f:x\mapsto A\cos \left(2x \right)+B\sin \left(2 x \right)$
- Or $f(0)= -1 \iff A\cos \left(0 \right)+B\sin \left(0 \right) = -1\iff A= -1$
- Comme $ f(x)= A\cos \left(2x \right)+B\sin \left(2 x \right)$ d'où on déduit $f'(x) =-2A\sin \left(2x \right)+2B\cos \left(2 x \right)$ et
- $f'0)= 2\iff 2B = 2 \iff B=1 $
- Ainsi, la solution $f$ de l'équation différentielle $y"+4 y=0$ qui vérifie $f(0)= -1$ et $f'(0)= 2$, est la fonction définie par $f(x)= -\cos \left(2x \right)+\sin \left(2 x \right)$.
- Comme pour tout réel $x$ on a $-1\leq \sin 2x\leq 1$ et $-1\leq \cos 2x\leq 1$, on en déduit que $-2\leq f(x)\leq 2$.
- Affirmation 3 : La solution de l'équation $\ln(x + 3) = 5$ est $\text{e}^5 - 3$. $$\begin{array}{rl} \ln(x + 3) = 5& \iff\text{ e} ^{\ln(x + 3)} = \text{ e} ^ 5 \\ & \iff x + 3 = \text{ e} ^ 5 \\ & \iff x = \text{ e} ^ 5 -3\\ \end{array}$$ L'affirmation 3 est vraie .
- La durée de vie en heures d'un certain type d'ampoules électriques est modélisée par une variable aléatoire qui suit la loi exponentielle de paramètre $\lambda = 0,000125 \: \left(\text{exprimé en } \:h\right)$.
Affirmation 4 : En moyenne, la durée de vie d'une ampoule est 1250 h. L'espérance de la variable aléatoire $X$ qui suit la loi exponentielle de paramètre $\lambda =0,000125$ est : $$E(X)=\dfrac{1}{\lambda}= \dfrac{1}{0,000125} =8000$$ L'affirmation 4 est fausse .
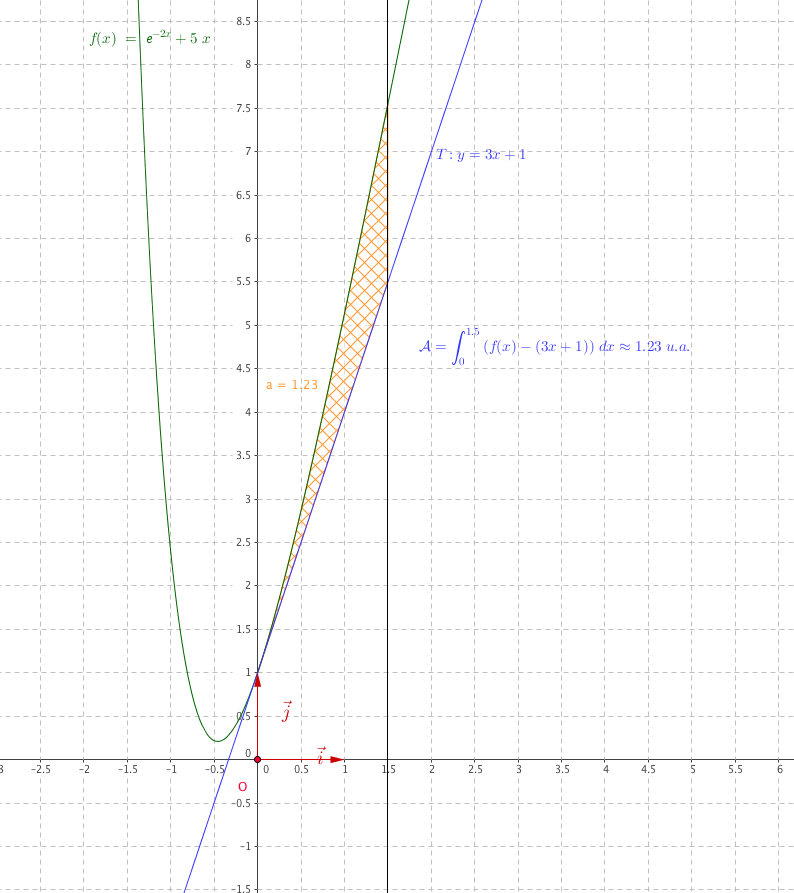
- Affirmation 5 : la fonction $F(x) = x\ln x - x + 2$ est une primitive de la fonction $f(x) = \ln x$ sur l'intervalle $]0~;~+\infty[$. $F$ est dérivable comme somme de deux fonctions dérivables.On écrit $F(x) = x\ln x - x + 2= x\left ( \ln x -1\right ) + 2 $ $F=u v ,$ d'où $F'=u'v+v'u $ avec pour tout réel $x$, dans $ ]0~;~+\infty[$ : $\left\{ \begin{array}{l} u(x)~ = x\\ v(x)~ = \ln x -1\end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ = 1\\ v'(x)~ = \dfrac{1}{x}\end{array}\right.$ $$ \begin{array}{cl} F'(x)& = 1\times (\ln x -1) + \times x \\ & = \ln x + 1 -1\\ &= \ln x = f(x) \end{array} $$ L'affirmation 5 est vraie .
L'affirmation 1 est vraie .
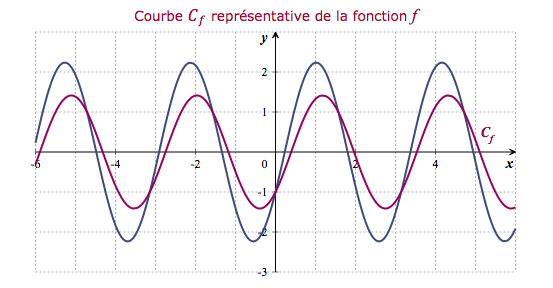 L'affirmation 2 est fausse .
L'affirmation 2 est fausse .
Exercice 3 4 points
Le bassin d'une piscine municipale a une capacité de 600000 litres d'eau. Afin de respecter les normes d'hygiène et de sécurité, 30000 litres d'eau de la piscine sont renouvelés chaque heure et le taux de chlore maximum autorisé est de $0,25$ mg/L.
Un soir après la fermeture de la piscine, alors que le taux de chlore est indétectable, $1$ kg de chlore est déversé par erreur dans le bassin à $20$ h.
Le directeur de la piscine souhaiterait savoir quand il pourra ouvrir à nouveau la piscine au public. On modélise la concentration massique du chlore présent dans la piscine par une fonction $f$. Lorsque $t$ désigne le temps écoulé depuis l'accident, exprimé en heures, $f(t)$ représente la concentration massique du chlore présent dans la piscine en milligrammes par litre. On admet que la fonction $f$ est solution de l'équation différentielle (E) : \[y' + 0,05 y = 0\quad \text{où }\: y \text{ désigne une fonction de la variable } t.\]
-
- Résoudre l'équation différentielle (E).
- Que vaut $f(0)$ ? En déduire une expression de $f(t)$ sur $[0~;~+ \infty[$.
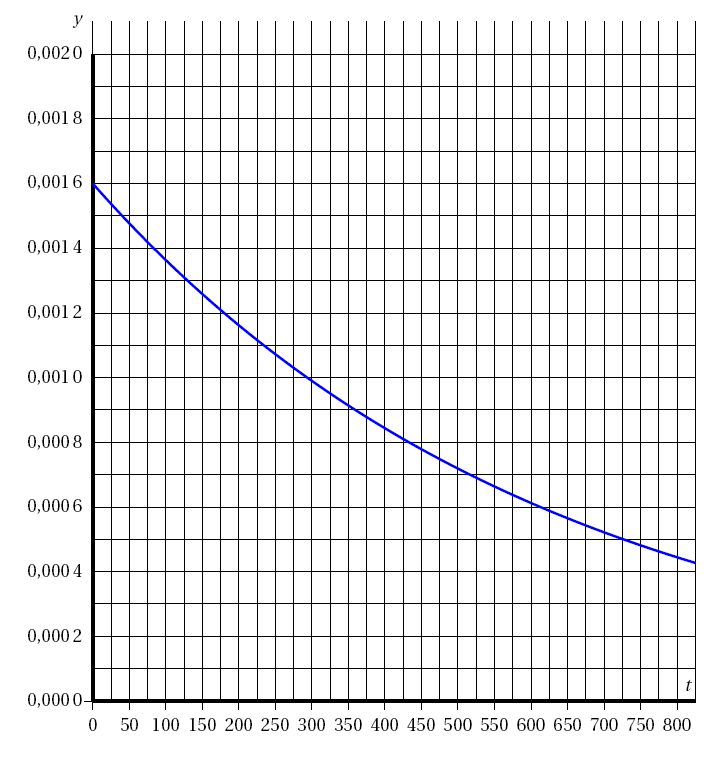
- On admet que $f$ est définie sur $[0~;~+ \infty[$ par $f(t) = \dfrac{5}{3} \times \text{e}^{- 0,05t}$. À quel moment la piscine pourra-t-elle ouvrir de nouveau au public ?
Correction de l'exercice 3 (4 points)
Le bassin d'une piscine municipale a une capacité de 600000 litres d'eau. Afin de respecter les normes d'hygiène et de sécurité, 30000 litres d'eau de la piscine sont renouvelés chaque heure et le taux de chlore maximum autorisé est de $0,25$ mg/L.
Un soir après la fermeture de la piscine, alors que le taux de chlore est indétectable, $1$ kg de chlore est déversé par erreur dans le bassin à $20$ h.
Le directeur de la piscine souhaiterait savoir quand il pourra ouvrir à nouveau la piscine au public. On modélise la concentration massique du chlore présent dans la piscine par une fonction $f$. Lorsque $t$ désigne le temps écoulé depuis l'accident, exprimé en heures, $f(t)$ représente la concentration massique du chlore présent dans la piscine en milligrammes par litre. On admet que la fonction $f$ est solution de l'équation différentielle (E) : \[y' + 0,05 y = 0\quad \text{où }\: y \text{ désigne une fonction de la variable } t.\]
-
- Résoudre l'équation différentielle (E). Les solutions de l'équation différentielle (E) : $y'+0,05 y=0$ , qui se met sous la forme $y'= - 0, 05 y$ ( type $y'=ay$ où $a=-0,05$) sont les fonctions $f$ de la forme $f:t\mapsto k e^{-0,05 t} $ où $k$ est un réel .
- Que vaut $f(0)$ ? En déduire une expression de $f(t)$ sur $[0~;~+ \infty[$. Au moment de l'accident, la concentration massique du chlore présent dans la piscine en milligrammes par litre est : $ \dfrac{10^6}{600000}=\dfrac{5}{3}$ Ainsi, $f(0) = \dfrac{5}{3}$ d'où $ k e^0=\dfrac{5}{3}$ soit $k=\dfrac{5}{3}$ La fonction $f$ est définie pour tout réel $t$ de l'intervalle $[0~;~+\infty[$ par $f(t)= \dfrac{5}{3} e^{-0,05 t} $.
- On admet que $f$ est définie sur $[0~;~+ \infty[$ par $f(t) = \dfrac{5}{3} \times \text{e}^{- 0,05t}$. À quel moment la piscine pourra-t-elle ouvrir de nouveau au public ? $$\begin{array}{rll} \dfrac{5}{3}\times e^{-0,05 t} \leq 0, 25& \iff e^{-0,05 t}\leq 0, 25\times \dfrac{3}{5} & \text{ on multiplie par } \dfrac{3}{5}> 0 \\ & \iff e^{-0,05 t}\leq \dfrac{1}{4}\times \dfrac{3}{5} & \\ & \iff e^{-0,05 t}\leq \dfrac{3}{20} & \\ & \iff \ln\left ( e^{-0,05 t}\right )\leq \ln\left ( \dfrac{3}{20}\right ) &\text{ on applique } \ln \\ &\iff -0,05 t \leq \ln\left ( \dfrac{3}{20}\right ) & \\ &\iff t\geq -\dfrac{ \ln\left ( \dfrac{3}{20}\right )}{0,05}& \text{ on divise par } -0,05< 0 \\ &\iff t\geq -20 \ln\left ( \dfrac{3}{20}\right ) & \end{array}$$ Comme $ -20 \ln\left ( \dfrac{3}{20}\right ) \approx 37,94$ , on en déduit que : La piscine pourra être ouverte au public 38 heures après le moment de l'accident.
Exercice 4 5 points
Les deux parties de cet exercice peuvent être traitées de manière indépendante. Dans l'ensemble de l'exercice, les résultats seront arrondis à $10^{-3}$ près. Une usine fabrique des batteries au lithium-ion pour des vélos électriques. Le cahier des charges indique qu'une batterie mesure 15 cm de large. Lors de la fabrication, on modélise la largeur des batteries par une variable aléatoire X qui suit une loi normale de moyenne $\mu = 15$ et d'écart-type $\sigma = 0,02$. L'objectif de cet exercice est d'analyser la qualité de la production dans cette usine.
Partie A
Une batterie est jugée conforme lorsque sa largeur, exprimée en centimètres, appartient à l'intervalle [14,95 ; 15,05].
- Calculer la probabilité qu'une batterie prélevée au hasard dans la production soit non conforme. L'usine vend ses batteries au lithium-ion par lots de 2000 aux fabricants de vélos électriques. En moyenne, chaque lot de 2000 batteries en contient $24$ non conformes. On note $p$ la probabilité qu'une batterie soit non conforme. On prélève au hasard 2000 batteries dans la production. La production est assez importante pour que l'on puisse assimiler ce prélèvement à un tirage aléatoire avec remise. On modélise le nombre de batteries non conformes dans un lot de 2000 par une variable aléatoire $Y$.
- Quelle loi suit la variable aléatoire $Y$ ? Préciser ses paramètres.
- Calculer la probabilité qu'il y ait au moins $30$ batteries non conformes dans un lot de 2000 batteries.
Partie B
Dans le cadre d'un fonctionnement correct des machines de la chaîne de production, on admet que la proportion $p$ de batteries non conformes est 1,2 %. Le responsable de l'usine affirme qu'il ne vend pas de lot de 2000 batteries qui en contienne plus de $40$ non conformes. Quelle est la fiabilité de cette affirmation ? Justifier.
Exercice 4 5 points
Les deux parties de cet exercice peuvent être traitées de manière indépendante. Dans l'ensemble de l'exercice, les résultats seront arrondis à $10^{-3}$ près. Une usine fabrique des batteries au lithium-ion pour des vélos électriques. Le cahier des charges indique qu'une batterie mesure 15 cm de large. Lors de la fabrication, on modélise la largeur des batteries par une variable aléatoire X qui suit une loi normale de moyenne $\mu = 15$ et d'écart-type $\sigma = 0,02$. L'objectif de cet exercice est d'analyser la qualité de la production dans cette usine.
Partie A
Une batterie est jugée conforme lorsque sa largeur, exprimée en centimètres, appartient à l'intervalle [14,95 ; 15,05].
- Calculer la probabilité qu'une batterie prélevée au hasard dans la production soit non conforme. L'usine vend ses batteries au lithium-ion par lots de 2000 aux fabricants de vélos électriques. En moyenne, chaque lot de 2000 batteries en contient $24$ non conformes. On note $p$ la probabilité qu'une batterie soit non conforme. On prélève au hasard 2000 batteries dans la production. La production est assez importante pour que l'on puisse assimiler ce prélèvement à un tirage aléatoire avec remise. On modélise le nombre de batteries non conformes dans un lot de 2000 par une variable aléatoire $Y$. Une batterie est non conforme lorsque sa largeur, exprimée en centimètres, n'appartient pas à l'intervalle $[14,95;15,05]$. $$P(X\notin [14,95;15,05]) =1-P(14,95\leq X \leq 15,05) \approx 0,012$$ On détaille un peu :
- Quelle loi suit la variable aléatoire $Y$ ? Préciser ses paramètres.
- Calculer la probabilité qu'il y ait au moins $30$ batteries non conformes dans un lot de 2000 batteries. La production est assez importante pour que l'on puisse assimiler le prélèvement de 2000 batteries à un tirage aléatoire avec remise donc :
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
Arrondie au millième près, la probabilité qu'une batterie prélevée au hasard dans la production soit non conforme est 0,012.
La variable aléatoire $Y$ suit la loi binomiale de paramètres $n=2000$ et $p=\dfrac{24}{2000}=0,012$.
Partie B
Dans le cadre d'un fonctionnement correct des machines de la chaîne de production, on admet que la proportion $p$ de batteries non conformes est 1,2 %. Le responsable de l'usine affirme qu'il ne vend pas de lot de 2000 batteries qui en contienne plus de $40$ non conformes. Quelle est la fiabilité de cette affirmation ? Justifier.
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
Avec un niveau de confiance de 95 % on accepte l'affirmation du responsable de l'usine.
- Vues: 19313