Bac STI2D Métropole 16 juin 2016
Exercice 1 4 points
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse.
Le plan complexe est rapporté à un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On note $\text{i}$ le nombre complexe vérifiant $\text{i}^2 =-1$
- Un argument du nombre complexe $2 + 2\text{i}$ est égal à :
- $-\dfrac{\pi}{4}$
- $-\dfrac{9\pi}{4}$
- $2\sqrt 2$
- $\dfrac{\pi}{4}$
- Le nombre complexe $\text{e}^{\text{i}\frac{\pi}{5}}\times \text{e}^{\text{i}\frac{2\pi}{15}}$ est égal à :
- $\frac{1}{2}+ \frac{\sqrt 3}{2}\text{i}$
- $\frac{\sqrt 3}{2}+\frac{1}{2} \text{i}$
- $0,5+0,866 \text{i}$
- $0,5+0,8660254038 \text{i}$
- On considère les points $A$ et $B$ d'affixes respectives $z_A = 2 \text{e}^{\text{i}\frac{\pi}{3}}$ et $z_B = \frac{5}{2} \text{e}^{\text{i}\frac{5\pi}{6}}$. Le triangle $OAB$ est :
- isocèle en $O$
- rectangle en $O$
- rectangle et isocèle en $B$
- isocèle en $B$
- Pour tout nombre réel $\theta$, le nombre complexe $\text{e}^{\text{i}\theta} +\dfrac{1}{\text{e}^{\text{i}\theta}} $ est égal à :
- $2\cos\left(\theta\right)$
- $\cos\left(\theta\right)+\text{i}\sin\left(\theta\right) $
- $1$
- $2\text{i}\sin\left(\theta\right)$
Correction de l'exercice 1 (4 points)
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse.
Le plan complexe est rapporté à un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$ On note $\text{i}$ le nombre complexe vérifiant $\text{i}^2 =-1$
- Un argument du nombre complexe $2 + 2\text{i}$ est égal à :
- $-\dfrac{\pi}{4}$
- $-\dfrac{9\pi}{4}$
- $2\sqrt 2$
- $\dfrac{\pi}{4}$
$2 + 2\text{i}$
- Module : \begin{align*} |z| & = \sqrt{ 2^2+2^2}\\ & = \sqrt{8}\\ & =2\sqrt{ 2 } \end{align*}
- Argument :
$$\left\lbrace \begin{array}{l} \cos \theta=\dfrac{a}{r}=\dfrac{2}{2\sqrt{ 2 }}= \dfrac{\sqrt 2 }{2} \\ \sin \theta=\dfrac{b}{r}=\dfrac{2}{2\sqrt{ 2 }}= \dfrac{\sqrt 2 }{2}\end{array} \right.$$ Donc $\theta = \dfrac{ \pi}{4}$ - On utilise la calculatrice :( en mode degré) pour les vieilles TI83 ...
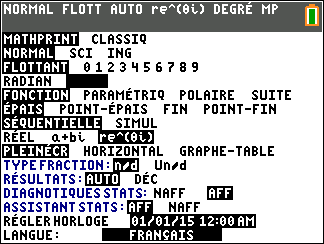
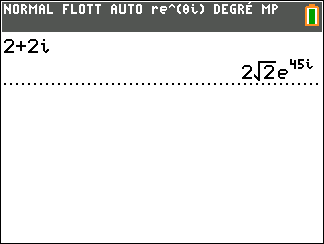
- Le nombre complexe $\text{e}^{\text{i}\frac{\pi}{5}}\times \text{e}^{\text{i}\frac{2\pi}{15}}$ est égal à :
- $\frac{1}{2}+ \frac{\sqrt 3}{2}\text{i}$
- $\frac{\sqrt 3}{2}+\frac{1}{2} \text{i}$
- $0,5+0,866 \text{i}$
- $0,5+0,8660254038 \text{i}$
\begin{align*} \text{e}^{\text{i}\frac{\pi}{5}}\times \text{e}^{\text{i}\frac{2\pi}{15}}&=\text{e}^{\text{i}\left (\frac{\pi}{5}+\frac{2\pi}{15}\right )}\\ & =\text{e}^{\text{i}\left (\frac{3\pi}{15}+\frac{2\pi}{15}\right )}\\ &=\text{e}^{\text{i}\frac{\pi}{3}}\\ &=\cos\left (\frac{\pi}{3}\right )+\text{i}\sin\left (\frac{\pi}{3}\right )\\ &=\frac{1}{2}+ \frac{\sqrt 3}{2}\text{i} \end{align*}
- On considère les points $A$ et $B$ d'affixes respectives $z_A = 2 \text{e}^{\text{i}\frac{\pi}{3}}$ et $z_B = \frac{5}{2} \text{e}^{\text{i}\frac{5\pi}{6}}$. Le triangle $OAB$ est :
- isocèle en $O$
- rectangle en $O$
- rectangle et isocèle en $B$
- isocèle en $B$
Plusieurs méthodes sont possibles ! On commence par faire une figure : - Pour tout nombre réel $\theta$, le nombre complexe $\text{e}^{\text{i}\theta} +\dfrac{1}{\text{e}^{\text{i}\theta}} $ est égal à :
- $2\cos\left(\theta\right)$
- $\cos\left(\theta\right)+\text{i}\sin\left(\theta\right) $
- $1$
- $2\text{i}\sin\left(\theta\right)$
\begin{align*} \text{e}^{\text{i}\theta} +\dfrac{1}{\text{e}^{\text{i}\theta}}&=\text{e}^{\text{i}\theta} +\text{e}^{-\text{i}\theta}& \text{ Prop.}\\ &=2\cos\left(\theta\right)&\text{ Première formule d'Euler}\\ \end{align*}
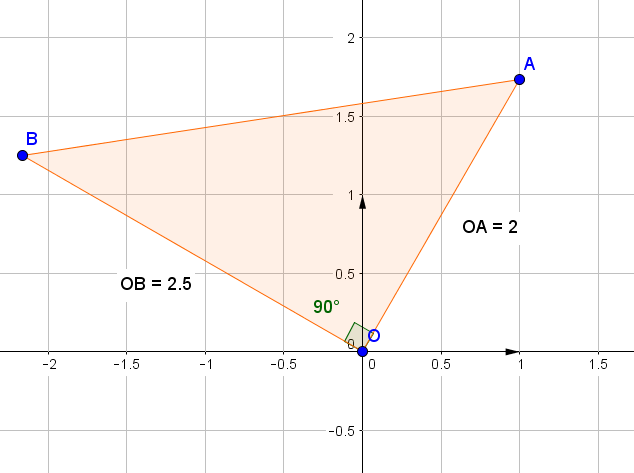
\begin{align*} z_A &= 2 \text{e}^{\text{i}\frac{\pi}{3}}\\ &=2\left (\cos\left (\frac{\pi}{3}\right )+\text{i}\sin\left (\frac{\pi}{3}\right )\right )\\ &=2\left (\frac{1}{2}+ \frac{\sqrt 3}{2}\text{i}\right )\\ &=1+\text{i}\sqrt 3\\ \text{Donc }& A(1, \sqrt 3) \end{align*} \begin{align*} z_B& =\frac{5}{2} \text{e}^{\text{i}\frac{5\pi}{6}}\\ &=\frac{5}{2}\left (\cos\left (\frac{5\pi}{6}\right )+\text{i}\sin\left (\frac{5\pi}{6}\right )\right )\\ &=\frac{5}{2}\left (\frac{\sqrt 3}{2}+ \text{i}\frac{1}{2}\right )\\ &=-\dfrac{5\sqrt 3}{4} +\text{i} \dfrac{5}{4}\\ \text{Donc }& B\left (-\dfrac{5\sqrt 3}{4}, \dfrac{5}{4}\right ) \end{align*} On a donc \begin{align*} z_{\vec{0A}} &=z_A-z_O\\ &=z_A\\ &=1+\text{i}\sqrt 3\\ \text{Donc }&\vec{0A} (1, \sqrt 3) \end{align*} \begin{align*} z_{\vec{0B}} &=z_B-z_O\\ &=z_B\\ &=-\dfrac{5\sqrt 3}{4} +\text{i} \dfrac{5}{4}\\ \text{Donc }& \vec{0B}\left (-\dfrac{5\sqrt 3}{4}, \dfrac{5}{4}\right ) \end{align*} Ainsi \begin{align*} \vec{0A}\cdot \vec{0B}& = XX' + YY'\\ &=1\times \left (-\dfrac{5\sqrt 3}{4}\right )+\sqrt 3 \times \dfrac{5}{4}\\ &=-\dfrac{5\sqrt 3}{4}+ \dfrac{5\sqrt 3}{4}\\ &=0 \end{align*} Ayant $\vec{0A}\cdot \vec{0B}=0$ les vecteurs $\vec{0A}$ et $ \vec{0B}$ sont orthogonaux, donc le triangle OAB est rectangle en $O$.
Exercice 2 6 points
Un centre de vacances possède une piscine de $600\quad m^3$ soit $600\quad 000$ litres. L'eau du bassin contient du chlore qui joue le rôle de désinfectant. Toutefois le chlore se dégrade et 25% de celui-ci disparaît chaque jour, en particulier sous l'effet des ultra-violets et de l'évaporation. Le 31 mai à 9 h, le responsable analyse l'eau du bassin à l'aide d'un kit distribué par un magasin spécialisé.
Le taux de chlore disponible dans l'eau est alors de 1,25 mg/L (milligrammes par litre).
Document
$$\begin{array}{|c|c|c|} \hline \text{Paramètres contrôlés} & \text{Seuils de qualité réglementaire} &\text{Incidences sur la qualité de l'eau} \\ \hline & \text{Au minimum 2 mg/L} & < \text{2 mg/L : sous chloration}\\ &&\text{Risque de prolifération}\\ && \text{bactérienne dans l eau }\\ \hline \text{Présence de Chlore }& \text{ Au maximum 4 mg/L }&\text{ > 4 mg/L : surchloration }\\ &&\text{Irritation de la peau}\\ \hline \end{array} $$
A partir du 1$^{\text{er}}$ juin pour compenser la perte en chlore, la personne responsable de l'entretien ajoute, chaque matin à 9 h, 570 g de chlore dans la piscine.
Pour le bien-être et la sécurité des usagers, le responsable souhaite savoir si cet apport journalier en chlore permettra de maintenir une eau qui respecte la réglementation donnée par l' Agence Régionale de Santé pour les piscines publiques.
Partie A
- Pour tout entier naturel $n$ on note $u_n$ la quantité de chlore disponible, exprimée en grammes, présente dans l'eau du bassin le $n^{\text{ième}}$ jour suivant le jour de l'analyse, immédiatement après l'ajout de chlore. Ainsi $u_0$ est la quantité de chlore le 31 mai à 9 h et $u_1$ est la quantité de chlore le 1$^{\text{er}}$ juin à 9 h après l'ajout de chlore.
- Montrer que la quantité de chlore, en grammes, présente dans l'eau du bassin le 31 mai à 9h est $u_0 = 750$.
Au regard des recommandations de l'agence régionale de santé, le responsable pouvait-il donner l'accès à la piscine le 31 mai? - Montrer que $u_1 = 1132,5$.
- Justifier que pour tout entier naturel $n, u_{n+1} = 0, 75u_n+ 570$
- La suite $(u_n)$ est-elle géométrique ?
- Montrer que la quantité de chlore, en grammes, présente dans l'eau du bassin le 31 mai à 9h est $u_0 = 750$.
- Soit l'algorithme ci-dessous : $$\begin{array}{|l |l |}\hline \text{Variables } & \\ &u : \text{un nombre réel }\\ &N : \text{un nombre entier naturel }\\ &k : \text{un nombre entier naturel }\\ \text{ Initialisation :}&\\ & \text{Saisir la valeur de } N \\ \text{ Initialisation :}&\\ & u \text{ prend la valeur } 750 \\ \text{ Traitement :}&\\ &\text{ Pour } k \text{ allant de } 1 \text{ à } N\\ &\hspace{0,5cm} u\text{ prend la valeur } 0,75 u +570\\ &\text{ Fin du Pour }\\ \text{ Sortie : }& \text{ Afficher } u \\ \hline \end{array}$$
- Quel est le rôle de cet algorithme ?
- Recopier et compléter le tableau suivant, par des valeurs exactes, en exécutant cet algorithme \og pas à pas »pour $N=3$. $$\begin{array}{|c|c|c|c|c|} \hline \text{Variables } & \text{ Initialisation }& \text{ Etape 1 } & \text{ Etape 2 } & \text{ Etape 3 } \\ \hline u & 750 &1132,5& & \\ \hline \end{array} $$ Au regard des recommandations de l'agence régionale de santé, au bout de combien de jours la piscine peut-elle être ouverte ?
- Calculer une valeur approchée à $10^{-3}$ près de la quantité de chlore le 15$^{\text{ième}}$ jour juste après l'ajout de chlore.
Partie B
Au fil du temps, la quantité de chlore évolue. On note $d_n$ l'écart de quantité de chlore d'un jour à l'autre en grammes. Pour tout entier naturel $n$, on a $d_n = u_{n+1}- u_n$.
-
- Calculer $d_0, d_1$ et $ d_2$. On donnera une valeur exacte.
- Justifier que $d_0, d_1$ et $ d_2$ semblent être les termes d'une suite géométrique.
- Vérifier que $u_{n+1}- u_n = -0,25u_n + 570$.
- On admet que pour tout entier naturel $n$, on a $d_{n+1}= 0, 75d_n$.
- Justifier que $d_n = 382,5 \times 0, 75^n$.
- En déduire que pour tout entier naturel $n$, on a $u_n = 2280 - 1530\times 0,75^n$.
- Déterminer la limite de la suite $(u_n)$. Interpréter le résultat trouvé.
Correction de l'exercice 2 (6 points)
Un centre de vacances possède une piscine de $600\quad m^3$ soit $600\quad 000$ litres. L'eau du bassin contient du chlore qui joue le rôle de désinfectant. Toutefois le chlore se dégrade et 25% de celui-ci disparaît chaque jour, en particulier sous l'effet des ultra-violets et de l'évaporation. Le 31 mai à 9 h, le responsable analyse l'eau du bassin à l'aide d'un kit distribué par un magasin spécialisé.
Le taux de chlore disponible dans l'eau est alors de 1,25 mg/L (milligrammes par litre).
Document
$$\begin{array}{|c|c|c|} \hline \text{Paramètres contrôlés} & \text{Seuils de qualité réglementaire} &\text{Incidences sur la qualité de l'eau} \\ \hline & \text{Au minimum 2 mg/L} & < \text{2 mg/L : sous chloration}\\ &&\text{Risque de prolifération}\\ && \text{bactérienne dans l eau }\\ \hline \text{Présence de Chlore }& \text{ Au maximum 4 mg/L }&\text{ > 4 mg/L : surchloration }\\ &&\text{Irritation de la peau}\\ \hline \end{array} $$
A partir du 1$^{\text{er}}$ juin pour compenser la perte en chlore, la personne responsable de l'entretien ajoute, chaque matin à 9 h, 570 g de chlore dans la piscine.
Pour le bien-être et la sécurité des usagers, le responsable souhaite savoir si cet apport journalier en chlore permettra de maintenir une eau qui respecte la réglementation donnée par l' Agence Régionale de Santé pour les piscines publiques.
Partie A
- Pour tout entier naturel $n$ on note $u_n$ la quantité de chlore disponible, exprimée en grammes, présente dans l'eau du bassin le $n^{\text{ième}}$ jour suivant le jour de l'analyse, immédiatement après l'ajout de chlore. Ainsi $u_0$ est la quantité de chlore le 31 mai à 9 h et $u_1$ est la quantité de chlore le 1$^{\text{er}}$ juin à 9 h après l'ajout de chlore.
- Montrer que la quantité de chlore, en grammes, présente dans l'eau du bassin le 31 mai à 9h est $u_0 = 750$.
Au regard des recommandations de l'agence régionale de santé, le responsable pouvait-il donner l'accès à la piscine le 31 mai? La quantité de chlore en milligrammes , présente dans l'eau du bassin le 31 mai à 9h est : \begin{align*} u_0&=1,25 \times 600\; 000\; \text{mg}\\ &=\dfrac{1,25 \times 600\; 000}{1\; 000}\; \text{g}\\ &= 750 \; \text{g} \end{align*} Ainsi $u_0 = 750$. - Montrer que $u_1 = 1132,5$. \begin{align*} u_1&=0,75\times u_0+570\\ &=1132,5 \end{align*}
- Justifier que pour tout entier naturel $n, u_{n+1} = 0, 75u_n+ 570$ On rappelle qu'une baisse de $t $ % revient à multiplier par $\left (1-\dfrac{t}{100}\right )$; ici la baisse de 25\% revient à multiplier par $\left (1-\dfrac{25}{100}\right )=0,75$
- La suite $(u_n)$ est-elle géométrique ? \begin{align*} u_0&=750&\\ u_1&=1132,5&\\ u_2&=0,75\times 1132,5+570&\\ &=1479,375&\\ \dfrac{u_1}{u_0}&=1,51&\dfrac{u_2}{u_1} =1,3063\\ \end{align*} Comme $\dfrac{u_1}{u_0}\neq \dfrac{u_2}{u_1}$, la suite $(u_n)$ n'est pas géométrique.
Au regard des recommandations de l'agence régionale de santé, le responsable ne pouvait pas donner l'accès à la piscine le 31 mai car le taux de 1,25 mg/L est inférieur à 2 mg/L .
On est dans un cas de sous chloration avec un risque de prolifération bactérienne.
$u_{n+1}=\underbrace{ 0,75 u_n}_{ \text{ Baisse de 25 %}}+\underbrace{570}_{\text{ Ajout quotidien de 570 g }}$ - Montrer que la quantité de chlore, en grammes, présente dans l'eau du bassin le 31 mai à 9h est $u_0 = 750$.
- Soit l'algorithme ci-dessous : $$\begin{array}{|l |l |}\hline \text{Variables } & \\ &u : \text{un nombre réel }\\ &N : \text{un nombre entier naturel }\\ &k : \text{un nombre entier naturel }\\ \text{ Initialisation :}&\\ & \text{Saisir la valeur de } N \\ \text{ Initialisation :}&\\ & u \text{ prend la valeur } 750 \\ \text{ Traitement :}&\\ &\text{ Pour } k \text{ allant de } 1 \text{ à } N\\ &\hspace{0,5cm} u\text{ prend la valeur } 0,75 u +570\\ &\text{ Fin du Pour }\\ \text{ Sortie : }& \text{ Afficher } u \\ \hline \end{array}$$
- Quel est le rôle de cet algorithme ? Cet algorithme permet de calculer les termes successifs de $(u_n)$ pour $n$ allant de 1 à $N$ et d'afficher en sortie $u_N$
- Recopier et compléter le tableau suivant, par des valeurs exactes, en exécutant cet algorithme \og pas à pas »pour $N=3$. $$\begin{array}{|c|c|c|c|c|} \hline \text{Variables } & \text{ Initialisation }& \text{ Etape 1 } & \text{ Etape 2 } & \text{ Etape 3 } \\ \hline u & 750 &1132,5& & \\ \hline \end{array} $$ Au regard des recommandations de l'agence régionale de santé, au bout de combien de jours la piscine peut-elle être ouverte ? $$\begin{array}{|c|c|c|c|c|} \hline \text{Variables } & \text{ Initialisation }& \text{ Etape 1 } & \text{ Etape 2 } & \text{ Etape 3 } \\ \hline u & 750 &1132,5& 1419,375 & 1634,53125 \\ \hline \end{array} $$
- Calculer une valeur approchée à $10^{-3}$ près de la quantité de chlore le 15$^{\text{ième}}$ jour juste après l'ajout de chlore. On utilise l'algorithme et on obtient $u_{15}\approx 2259, 554$
Au regard des recommandations de l'agence régionale de santé, au bout de combien de jours la piscine peut-elle être ouverte ?Au bout d'un jour le taux de chlore disponible dans l'eau est alors de $\dfrac{1132,5}{600}\approx 1,89$ mg/L . Au bout de deux jours le taux de chlore disponible dans l'eau est alors de $\dfrac{1419,375,5}{600}\approx 2,37$ mg/L .
La piscine pourra donc être ouverte au bout de deux jours.
Partie B
Au fil du temps, la quantité de chlore évolue. On note $d_n$ l'écart de quantité de chlore d'un jour à l'autre en grammes. Pour tout entier naturel $n$, on a $d_n = u_{n+1}- u_n$.
-
- Calculer $d_0, d_1$ et $ d_2$. On donnera une valeur exacte. \begin{align*} d_0 &= u_{1}- u_0&=382,5\\ d_1 &= u_{2}- u_1&=286,875\\ d_2 &= u_{2}- u_1&=215,15625\\ \end{align*}
- Justifier que $d_0, d_1$ et $ d_2$ semblent être les termes d'une suite géométrique. On a $\dfrac{d_1}{d_0}=0,75$ et $\dfrac{d_2}{d_1}=0,75$,
$d_0, d_1$ et $ d_2$ semblent être les termes d'une suite géométrique de raison $0,75$. - Vérifier que $u_{n+1}- u_n = -0,25u_n + 570$. \begin{align*} u_{n+1}- u_n&=0, 75u_n+ 570-u_n\\ &= -0, 25u_n+ 570 \end{align*}
- On admet que pour tout entier naturel $n$, on a $d_{n+1}= 0, 75d_n$.
- Justifier que $d_n = 382,5 \times 0, 75^n$. Ayant pour tout entier naturel $n$, on a $d_{n+1}= 0, 75d_n$, la suite $(d_n)$ est géométrique de raison $q=0,75$, de premier termerme $d_0=382,5$,
- En déduire que pour tout entier naturel $n$, on a $u_n = 2280 - 1530\times 0,75^n$. $u_{n+1}- u_n = -0,25u_n + 570$ et $d_n = u_{n+1}- u_n$, on adonc
- Déterminer la limite de la suite $(u_n)$. Interpréter le résultat trouvé. Comme $01< 0,75 < 1$ on déduit $\lim\limits_{n\to +\infty}0,75^n=0$ et donc $\lim\limits_{n\to +\infty}u_n=2280$
\begin{align*} d_n&=q^n \times d_0\\ &= 382,5 \times 0, 75^n \end{align*}
$d_n = -0,25u_n + 570$, \begin{align*} d_n = -0,25u_n + 570&\iff -0,25 u_n=d_n-570\\ &\iff -4\times -0,25 u_n=-4\times \left (d_n-570\right )\\ &\iff u_n= -4d_n +2280\\ &\iff u_n=-4\times 382,5 \times 0, 75^n +2280\\ &\iff u_n= 2280 - 1530\times 0,75^n \end{align*}
Le taux de chlore au bout d'un grand nombre de jours sera très proche de $\dfrac{2280}{600}=3,8$.
Ce taux étant compris entre 2 mg/L et 4 mg/L, la situation sera stable ! On pourra donc laisser la piscine ouverte ...
Exercice 3 4 points
Quand l'oreille humaine est soumise à une intensité acoustique, exprimée en watts par mètre carré (W/m$^2$), le niveau sonore du bruit responsable de cette intensité acoustique est exprimé en décibels (dB).
Document
\[\begin{array}{|c|c|c|c|}\hline \text{Sources sonores} &\text{Intensité} &\text{Niveau} & \text{Sensation auditive} \\ &\text{acoustique} &\text{sonore} &\\ &\text{(W/m}^2\text{ )} &\text{arrondi} & \\ & &\text{éventuellement}&\\ & &\text{à l'unité} &\\\hline \text{Décollage de la Fusée Ariane}& 10^ 6 &180 &\text{Exige une protection spéciale} \\ \hline \text{Turboréacteur} & 10^2 &140 &\text{Exige une protection spéciale} \\ \hline \text{Course de Formule 1} & 10 &130 &\text{Exige une protection spéciale} \\ \hline \text{Avion au décollage} & 1 &120 &\text{Seuil de douleur} \\ \hline \text{Concert et discothèque} & 10^{-1} &110 &\text{Très difficilement supportable} \\ \hline \text{Baladeur à puissance}& 10^{-2} &100 & \text{Très difficilement supportable} \\ \text{ maximum } & & &\\ \hline \text{ Moto} & 10^{-5} & 70 &\text{Pénible à entendre} \\ \hline \text{ Voiture au ralenti}&10^{-7} & 50 &\text{Bruit courant}\\ \hline \text{Seuil d'audibilité} & 10^{-12} & 0,08 &\text{Silence anormal} \\ \hline \end{array}\]
- D'après le tableau, lorsque l'intensité acoustique est multipliée par 10, quelle semble être l'augmentation du niveau sonore ?
- La relation liant l'intensité acoustique $x$ où $x$ appartient à l'intervalle $\left [10^ {-12} ; 10^6\right ]$ et le niveau sonore est donnée par : $$f (x) =\dfrac{10}{\ln 10} \times \ln(x) + 120.$$ On pourra prendre $\dfrac{10}{\ln 10} \approx 4,34$.
- Vérifier la conjecture émise à la question 1.
- Quel serait le niveau sonore de deux motos ?
- Pour éviter tout risque sur la santé, le port d'un casque de protection acoustique est donc conseillé au delà de 85 dB. Déterminer l'intensité acoustique à partir de laquelle le port d'un tel casque est conseillé.
Correction de l'exercice 3 (4 points)
Quand l'oreille humaine est soumise à une intensité acoustique, exprimée en watts par mètre carré (W/m$^2$), le niveau sonore du bruit responsable de cette intensité acoustique est exprimé en décibels (dB).
Document
\[\begin{array}{|c|c|c|c|}\hline \text{Sources sonores} &\text{Intensité} &\text{Niveau} & \text{Sensation auditive} \\ &\text{acoustique} &\text{sonore} &\\ &\text{(W/m}^2\text{ )} &\text{arrondi} & \\ & &\text{éventuellement}&\\ & &\text{à l'unité} &\\\hline \text{Décollage de la Fusée Ariane}& 10^ 6 &180 &\text{Exige une protection spéciale} \\ \hline \text{Turboréacteur} & 10^2 &140 &\text{Exige une protection spéciale} \\ \hline \text{Course de Formule 1} & 10 &130 &\text{Exige une protection spéciale} \\ \hline \text{Avion au décollage} & 1 &120 &\text{Seuil de douleur} \\ \hline \text{Concert et discothèque} & 10^{-1} &110 &\text{Très difficilement supportable} \\ \hline \text{Baladeur à puissance}& 10^{-2} &100 & \text{Très difficilement supportable} \\ \text{ maximum } & & &\\ \hline \text{ Moto} & 10^{-5} & 70 &\text{Pénible à entendre} \\ \hline \text{ Voiture au ralenti}&10^{-7} & 50 &\text{Bruit courant}\\ \hline \text{Seuil d'audibilité} & 10^{-12} & 0,08 &\text{Silence anormal} \\ \hline \end{array}\]
- D'après le tableau, lorsque l'intensité acoustique est multipliée par 10, quelle semble être l'augmentation du niveau sonore ? D'après le tableau, lorsque l'intensité acoustique est multipliée par 10, on semble ajouter 10 dB au niveau sonore.
- La relation liant l'intensité acoustique $x$ où $x$ appartient à l'intervalle $\left [10^ {-12} ; 10^6\right ]$ et le niveau sonore est donnée par : $$f (x) =\dfrac{10}{\ln 10} \times \ln(x) + 120.$$ On pourra prendre $\dfrac{10}{\ln 10} \approx 4,34$.
- Vérifier la conjecture émise à la question 1. \begin{align*} f(10x) & = \dfrac{10}{\ln 10} \times \ln(10 x) + 120& \text{ On a multiplié par 10 ... }\\ &=\dfrac{10}{\ln 10} \times \left ( \ln(10) +\ln ( x) \right )+ 120& \\ &=\dfrac{10}{\ln 10} \times \left ( \ln 10 +\ln ( x) \right )+ 120& \\ &=\dfrac{10}{\ln 10} \times \ln 10 + \dfrac{10}{\ln 10} \times \ln x + 120 \\ &= 10 + \underbrace{\dfrac{10}{\ln 10} \times \ln x + 120 }_{f(x)}\\ &= f(x)+ 10 \end{align*}
- Quel serait le niveau sonore de deux motos ? Pour calculer le le niveau sonore de deux motos on calcule $f\left ( 2\times 10^{-5}\right )$ \begin{align*} f\left ( 2\times 10^{-5}\right ) & = \dfrac{10}{\ln 10} \times \ln\left ( 2\times 10^{-5}\right ) + 120& \\ &=\dfrac{10}{\ln 10} \times \left ( \ln2 +\ln \left ( 10^{-5}\right ) \right )+ 120& \text{ car } \ln (a \times b)= \ln a +\ln b \\ &=\dfrac{10}{\ln 10} \times \ln 2 + \dfrac{10}{\ln 10} \times \left ( 10^{-5}\right ) + 120 \\ &= \dfrac{10\ln 2}{\ln 10} + \underbrace{ \dfrac{10}{\ln 10} \times \left ( 10^{-5}\right ) + 120 }_{f\left ( 10^{-5}\right )}\\ &= \dfrac{10\ln 2}{\ln 10} +70 \\ &\approx 73 \end{align*} Remarque: on peut bien sûr vérifier ce calcul à l'aide d'une calculatrice !
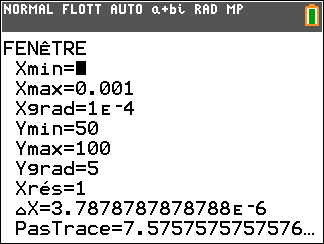
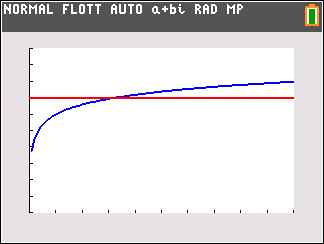
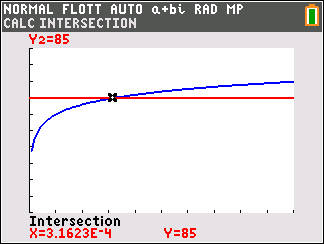
Le niveau sonore de deux motos est environ 73 dB. - Pour éviter tout risque sur la santé, le port d'un casque de protection acoustique est donc conseillé au delà de 85 dB. Déterminer l'intensité acoustique à partir de laquelle le port d'un tel casque est conseillé. On résout $f(x) < 85$ \begin{align*} f(x) < 85 & \iff \dfrac{10}{\ln 10} \times \ln(x) + 120 < 85 & \\ & \iff \dfrac{10}{\ln 10} \times \ln(x) < -35 & \\ & \iff \ln x < -\dfrac{ 35 \ln 10 }{10} & \text{ car } \dfrac{10}{\ln 10} \approx 4,34 > 0 \\ &\iff x < \text{e}^{ -\frac{35 \ln 10 }{10} } & \text{ car } x \mapsto \text{e}^x \text{ est st. croissante sur } \mathbb R \\ &\iff x < \left (\text{e}^{ \ln 10 } \right )^{-\frac{35}{10}}& \\ &\iff x < 10^{-3,5} \end{align*} Or $10^{-3,5}\approx 3,2 \times 10^{-4}$
L'intensité acoustique à partir de laquelle le port d'un tel casque est conseillé est environ $3,2 \times 10^{-4}$ W/m$^2$. On résout $f(x) < 85$
On utilise la calculatrice :
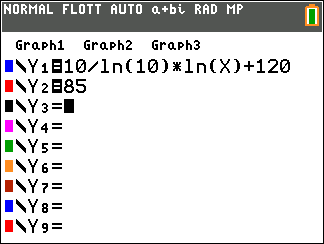
|
|
|
|
|
Exercice 4 6 points
Les parties A et B sont indépendantes.
Un pont levant enjambant un canal peu fréquenté est constitué d'un tablier qui, une fois relevé, permet le passage de bateaux de différentes tailles. 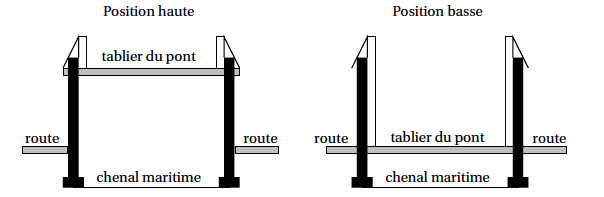
$$\begin{array}{|l |} \hline \text{Hauteur du tablier en position haute : 7 mètres}\\ \text{Longueur du tablier : 30 mètres}\\ \text{Temps de montée du tablier : 2 minutes}\\ \text{Temps en position haute du tablier (hors incident) : 8 minutes}\\ \text{Temps de descente du tablier : 2 minutes}\\ \hline \end{array} $$
Partie A - Sur la route
Un automobiliste se présente devant le pont. Le tablier du pont est en position haute. On s'intéresse ici au temps d'attente D, exprimé en minutes, de l'automobiliste avant qu'il puisse franchir le canal, pont baissé (hors incident).
- Combien de temps l'automobiliste attend-il au minimum ? au maximum?
- On admet que le temps d'attente, en minutes, de l'automobiliste pour franchir le pont est une variable aléatoire D qui suit la loi uniforme sur l'intervalle [2 ;10].
Déterminer l'espérance E(D) de la variable aléatoire D et interpréter le résultat dans le contexte. - Calculer la probabilité que le temps d'attente de l'automobiliste ne dépasse pas 5 minutes.
Partie B - Sur l'eau
Dans cette partie les résultats demandés seront arrondis à $10^ {-2}$ près.
Lorsqu'un bateau est passé, le tablier du pont revient en position basse. Le temps, exprimé en heures, avant que le bateau suivant se présente devant le pont est une variable aléatoire T qui suit la loi exponentielle de paramètre $\lambda = 0,05$. Ce temps est appelé temps de latence.
- Déterminer l'espérance E(T) de la variable aléatoire T et interpréter le résultat dans le contexte.
- On considère la fonction $f$ définie sur $[0 , +\infty[$ par $f (x) = 0,05 \text{e}^{-0,05 x}$.
- Montrer que la fonction $F$ définie sur$[0 , +\infty[$ par $F(x) =-\text{e}^{-0,05 x}$ est une primitive de $ f$ .
- On rappelle que pour tout nombre réel $t$ de $[0 , +\infty[ , P(T \leq t) = \displaystyle\int_0 ^t f(x)\; dx$.
Démontrer que $P(T \leq t) =1- \text{e}^{-0,05 t}$.
-
- Calculer la probabilité que le temps de latence soit inférieur à une demi-journée, soit 12 heures.
- Calculer la probabilité que le temps de latence soit supérieur à un jour.
- Calculer $P(12\leq T\leq 24)$.
Exercice 4 6 points
Les parties A et B sont indépendantes.
Un pont levant enjambant un canal peu fréquenté est constitué d'un tablier qui, une fois relevé, permet le passage de bateaux de différentes tailles. 
$$\begin{array}{|l |} \hline \text{Hauteur du tablier en position haute : 7 mètres}\\ \text{Longueur du tablier : 30 mètres}\\ \text{Temps de montée du tablier : 2 minutes}\\ \text{Temps en position haute du tablier (hors incident) : 8 minutes}\\ \text{Temps de descente du tablier : 2 minutes}\\ \hline \end{array} $$
Partie A - Sur la route
Un automobiliste se présente devant le pont. Le tablier du pont est en position haute. On s'intéresse ici au temps d'attente D, exprimé en minutes, de l'automobiliste avant qu'il puisse franchir le canal, pont baissé (hors incident).
- Combien de temps l'automobiliste attend-il au minimum ? au maximum? Le tablier du pont étant en position haute, l'automobiliste attendra au minimum 2 minutes (Temps de montée du tablier )
- On admet que le temps d'attente, en minutes, de l'automobiliste pour franchir le pont est une variable aléatoire D qui suit la loi uniforme sur l'intervalle [2 ;10].
Déterminer l'espérance E(D) de la variable aléatoire D et interpréter le résultat dans le contexte. Rappel : Si D suit la loi uniforme sur $[a; b]$ alors l'espérance E(D)=$\dfrac{a+b}{2}$ \begin{align*} E(D)&=\dfrac{2+10}{2}\\ &=6 \end{align*} - Calculer la probabilité que le temps d'attente de l'automobiliste ne dépasse pas 5 minutes. On calcule ici $P(D\leq 5)$ \begin{align*} P(D\leq 5)&=\dfrac{\text{longueur } [ 2~; ~5] }{\text{longueur } [ 2~; ~8]}\\ &= \dfrac{5-2}{10-2}\\ &=\dfrac{3}{8} \end{align*} La probabilité que le temps d'attente de l'automobiliste ne dépasse pas 5 minutes est 0,375.
Au maximum, l'automobiliste attendra 10 minutes (Temps en position haute du tablier (hors incident) : 8 minutes +Temps de descente du tablier + 2 minutes)
Le temps d'attente moyen, en minutes, de l'automobiliste pour franchir le pont est de 6 minutes .
Partie B - Sur l'eau
Dans cette partie les résultats demandés seront arrondis à $10^ {-2}$ près.
Lorsqu'un bateau est passé, le tablier du pont revient en position basse. Le temps, exprimé en heures, avant que le bateau suivant se présente devant le pont est une variable aléatoire T qui suit la loi exponentielle de paramètre $\lambda = 0,05$. Ce temps est appelé temps de latence.
- Déterminer l'espérance E(T) de la variable aléatoire T et interpréter le résultat dans le contexte. T suit une loi exponentielle donc son espérance mathématique vaut : \begin{align*} E(T)&=\dfrac{1}{\lambda}\\ &=\dfrac{1}{0,05}\\ & = 20 \end{align*} Le temps moyen avant que le bateau suivant se présente devant le pont est de 20 heures.
- On considère la fonction $f$ définie sur $[0 , +\infty[$ par $f (x) = 0,05 \text{e}^{-0,05 x}$.
- Montrer que la fonction $F$ définie sur$[0 , +\infty[$ par $F(x) =-\text{e}^{-0,05 x}$ est une primitive de $ f$ . Il suffit de vérifier que la dérivée de $F$ est $f$ \begin{align*} F'(x)&=-\left (-0,05\text{e}^{-0,05 x}\right )\\ &=0,05\text{e}^{-0,05 x}\\ &=f(x) \end{align*} $F$ définie sur$[0 , +\infty[$ par $F(x) =-\text{e}^{-0,05 x}$ est donc une primitive de $ f$ .
- On rappelle que pour tout nombre réel $t$ de $[0 , +\infty[ , P(T \leq t) = \displaystyle\int_0 ^t f(x)\; dx$.
Démontrer que $P(T \leq t) =1- \text{e}^{-0,05 t}$. \begin{align*} P(T \leq t) & = \displaystyle\int_0 ^t f(x)\; dx\\ &=F(t)-F(0)\\ &=-\text{e}^{-0,05 t}-\left (-\text{e}^{0}\right )\\ &=1- \text{e}^{-0,05 t} \end{align*}
-
- Calculer la probabilité que le temps de latence soit inférieur à une demi-journée, soit 12 heures. \begin{align*} P(T \leq 12) & =1- \text{e}^{-0,05 \times 12}\\ &= 1- \text{e}^{-0,6}\\ &\approx 0,45 \end{align*}
- Calculer la probabilité que le temps de latence soit supérieur à un jour. On calcule donc $P(T\geq 24)$ \begin{align*} P(T\geq 24)&=1-P(T<24)\\ &=1-P(T\leq 24)\\ &=1-\left ( 1- \text{e}^{-0,05 \times 24}\right )\\ &= \text{e}^{-1,2}\\ & \approx 0,30 \end{align*}
- Calculer $P(12\leq T\leq 24)$. \begin{align*} P(12\leq T\leq 24) & = \displaystyle\int_{12} ^{24} f(x)\; dx\\ &=F(24)-F(12)\\ &=-\text{e}^{-0,05 \times 24}-\left (-\text{e}^{-0,05 \times 12}\right )\\ &=\text{e}^{-0,6}-\text{e}^{-1,2}\\ &\approx 0,25 \end{align*}
- Vues: 20932
