Bac STI2D Métropole 16 juin 2016 - Correction Exercice 3
Correction de l'exercice 3 (4 points)
Quand l'oreille humaine est soumise à une intensité acoustique, exprimée en watts par mètre carré (W/m$^2$), le niveau sonore du bruit responsable de cette intensité acoustique est exprimé en décibels (dB).
Document
\[\begin{array}{|c|c|c|c|}\hline \text{Sources sonores} &\text{Intensité} &\text{Niveau} & \text{Sensation auditive} \\ &\text{acoustique} &\text{sonore} &\\ &\text{(W/m}^2\text{ )} &\text{arrondi} & \\ & &\text{éventuellement}&\\ & &\text{à l'unité} &\\\hline \text{Décollage de la Fusée Ariane}& 10^ 6 &180 &\text{Exige une protection spéciale} \\ \hline \text{Turboréacteur} & 10^2 &140 &\text{Exige une protection spéciale} \\ \hline \text{Course de Formule 1} & 10 &130 &\text{Exige une protection spéciale} \\ \hline \text{Avion au décollage} & 1 &120 &\text{Seuil de douleur} \\ \hline \text{Concert et discothèque} & 10^{-1} &110 &\text{Très difficilement supportable} \\ \hline \text{Baladeur à puissance}& 10^{-2} &100 & \text{Très difficilement supportable} \\ \text{ maximum } & & &\\ \hline \text{ Moto} & 10^{-5} & 70 &\text{Pénible à entendre} \\ \hline \text{ Voiture au ralenti}&10^{-7} & 50 &\text{Bruit courant}\\ \hline \text{Seuil d'audibilité} & 10^{-12} & 0,08 &\text{Silence anormal} \\ \hline \end{array}\]
- D'après le tableau, lorsque l'intensité acoustique est multipliée par 10, quelle semble être l'augmentation du niveau sonore ? D'après le tableau, lorsque l'intensité acoustique est multipliée par 10, on semble ajouter 10 dB au niveau sonore.
- La relation liant l'intensité acoustique $x$ où $x$ appartient à l'intervalle $\left [10^ {-12} ; 10^6\right ]$ et le niveau sonore est donnée par : $$f (x) =\dfrac{10}{\ln 10} \times \ln(x) + 120.$$ On pourra prendre $\dfrac{10}{\ln 10} \approx 4,34$.
- Vérifier la conjecture émise à la question 1. \begin{align*} f(10x) & = \dfrac{10}{\ln 10} \times \ln(10 x) + 120& \text{ On a multiplié par 10 ... }\\ &=\dfrac{10}{\ln 10} \times \left ( \ln(10) +\ln ( x) \right )+ 120& \\ &=\dfrac{10}{\ln 10} \times \left ( \ln 10 +\ln ( x) \right )+ 120& \\ &=\dfrac{10}{\ln 10} \times \ln 10 + \dfrac{10}{\ln 10} \times \ln x + 120 \\ &= 10 + \underbrace{\dfrac{10}{\ln 10} \times \ln x + 120 }_{f(x)}\\ &= f(x)+ 10 \end{align*}
- Quel serait le niveau sonore de deux motos ? Pour calculer le le niveau sonore de deux motos on calcule $f\left ( 2\times 10^{-5}\right )$ \begin{align*} f\left ( 2\times 10^{-5}\right ) & = \dfrac{10}{\ln 10} \times \ln\left ( 2\times 10^{-5}\right ) + 120& \\ &=\dfrac{10}{\ln 10} \times \left ( \ln2 +\ln \left ( 10^{-5}\right ) \right )+ 120& \text{ car } \ln (a \times b)= \ln a +\ln b \\ &=\dfrac{10}{\ln 10} \times \ln 2 + \dfrac{10}{\ln 10} \times \left ( 10^{-5}\right ) + 120 \\ &= \dfrac{10\ln 2}{\ln 10} + \underbrace{ \dfrac{10}{\ln 10} \times \left ( 10^{-5}\right ) + 120 }_{f\left ( 10^{-5}\right )}\\ &= \dfrac{10\ln 2}{\ln 10} +70 \\ &\approx 73 \end{align*} Remarque: on peut bien sûr vérifier ce calcul à l'aide d'une calculatrice !
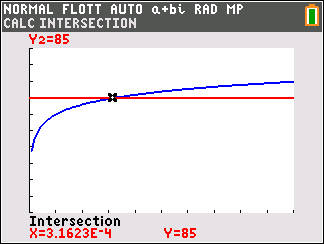
Le niveau sonore de deux motos est environ 73 dB. - Pour éviter tout risque sur la santé, le port d'un casque de protection acoustique est donc conseillé au delà de 85 dB. Déterminer l'intensité acoustique à partir de laquelle le port d'un tel casque est conseillé. On résout $f(x) < 85$ \begin{align*} f(x) < 85 & \iff \dfrac{10}{\ln 10} \times \ln(x) + 120 < 85 & \\ & \iff \dfrac{10}{\ln 10} \times \ln(x) < -35 & \\ & \iff \ln x < -\dfrac{ 35 \ln 10 }{10} & \text{ car } \dfrac{10}{\ln 10} \approx 4,34 > 0 \\ &\iff x < \text{e}^{ -\frac{35 \ln 10 }{10} } & \text{ car } x \mapsto \text{e}^x \text{ est st. croissante sur } \mathbb R \\ &\iff x < \left (\text{e}^{ \ln 10 } \right )^{-\frac{35}{10}}& \\ &\iff x < 10^{-3,5} \end{align*} Or $10^{-3,5}\approx 3,2 \times 10^{-4}$
L'intensité acoustique à partir de laquelle le port d'un tel casque est conseillé est environ $3,2 \times 10^{-4}$ W/m$^2$. On résout $f(x) < 85$
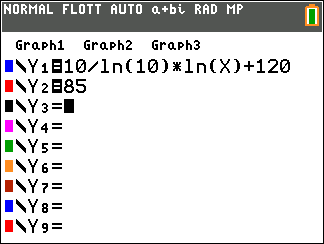
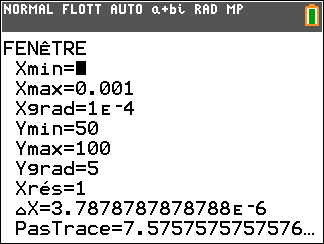
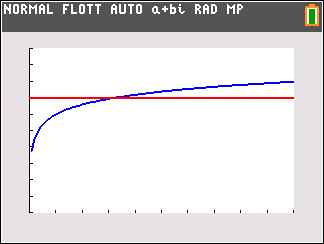
On utilise la calculatrice :
|
|
|
|
|
- Vues: 21427
