Bac STI2D Métropole 18 juin 2015 - Correction Exercice 4

Page 8 sur 8: Correction Exercice 4

Exercice 4 5 points

Probabilités

Dans l'ensemble de l'exercice, les résultats seront arrondis à $10^{-4}$ près. L'usine OCEFRAIS embouteille des jus de fruits. L'étiquette de la bouteille indique 1,5 litre de jus de fruits. Le volume de la bouteille est de 1,55 litre.
A l'embouteillage, le volume de jus de fruits versé dans une bouteille est une variable aléatoire $X$ qui suit la loi normale de moyenne $\mu = 1,5$ et d’écart-type $\sigma = 0,015$.

1. 1. L'une des trois figures donne la courbe représentative $\mathcal{C}_f$ de la densité $f$ de cette loi normale. Indiquer sur la copie le numéro de la figure correspondante en expliquant votre choix.
      
      

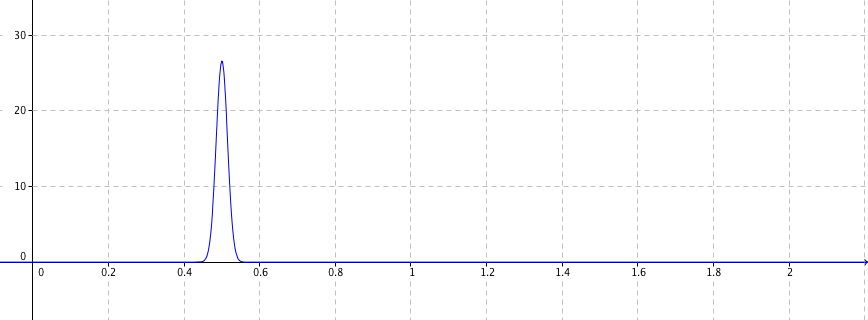
      Figure 1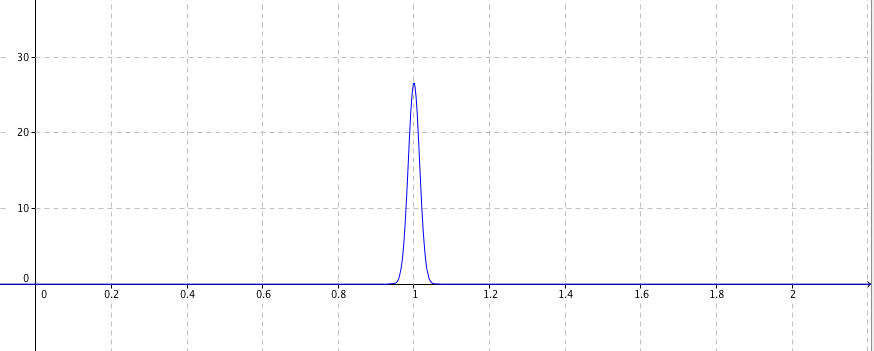

      Figure 2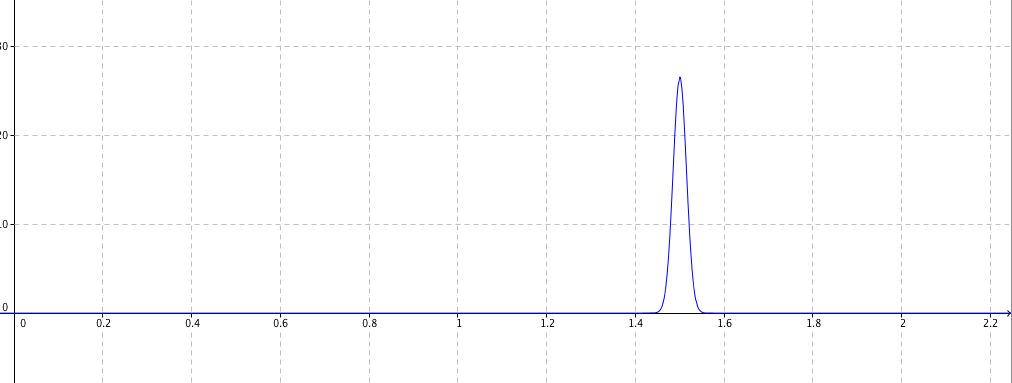

      Figure 3

   On sait que la courde de la densité de probabilité d'une loi normale $\mathcal{N}(\mu;\sigma)$ est symétrique par rapport à la droite d'équation $x=\mu$. Ici $\mu=1,5$ , donc la figure 3 est la la courbe représentative $\mathcal{C}_f$ de la densité $f$ de cette loi normale.
   2. Déterminer $P(1,485\leq X\leq 1,515)$.

   2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

   $$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

    

2. On choisit au hasard une bouteille de jus de fruits.
   1. Quelle est la probabilité que cette bouteille contienne exactement 1,48 litre de jus de fruits ?
   On veut ici $$P(X=148)= \displaystyle\int_{148}^{148}f(t)\;dt= 0$$
   2. Calculer la probabilité que cette bouteille contienne entre 1,46 litre et 1,54 litre de jus de fruits.
   On calcule $P(1,46\leq X\leq 1,54)$

   2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

   $$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

    

   3. Quelle est la probabilité que cette bouteille déborde sur la chaîne d'embouteillage?
      On rappelle que toutes les bouteilles utilisées ont un volume de 1,55 litre.
   On veut donc ici calculer $P(X\geq 1,55)$

    

   2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$

   $$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
3. Une bouteille est dite conforme si elle contient entre 1,46 litre et 1,54 litre de jus de fruits. Selon l'usine OCEFRAIS, la probabilité qu'une bouteille soit non conforme est 0,0077. Un supermarché achète un lot de 10 000 bouteilles.
   1. Déterminer l'intervalle de fluctuation asymptotique à 95% de la fréquence observée de bouteilles non conformes dans un tel lot.
   On calcule tout d'abord la probabilité qu'une bouteille soit non conforme  $p = 1 - P(1,46\leq X\leq 1,54)\approx 0,0077$

   La proportion $p$ est égale à  $\1$. La taille  $n$  de l'échantillon considéré est égale à  $\2.$
   Comme  $ n =\2$ ,   $n \times p  $=\3  et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.

   En effet on a bien : $$n \geq 30\;;\; n \times p \geq 5 \text{ et } n\times (1-p) \geq 5$$

   
   L'intervalle de fluctuation asymptotique au seuil de  $95\% $  est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$ 

   $$I_{10000}=[0,0060; 0,0094]$$
   2. Dans le lot de 10 000 bouteilles, on a compté 90 bouteilles non conformes. Le gérant du supermarché trouve le nombre de bouteilles non conformes anormalement élevé.
      L'usine OCEFRAIS a-t-elle des raisons de s'inquiéter?
   On utilise la règle de décision suivante :
   • On calcule la fréquence de bouteilles non conformes sur un échantillon de 10 000 bouteilles ; ici $f_{obs}= \dfrac{90}{10 000}= 0,009$
   • Si $f_{obs}\in I_{10000}$, on affirme que l'usine OCEFRAIS n'a pas raison de s'inquiéter.
   • Si $f_{obs}\notin I_{10000}$, on affirme que l'usine OCEFRAIS n'a pas raison de s'inquiéter.
   Ici $0,009\in [0,0060; 0,0094]$, et donc l'usine OCEFRAIS n'a pas raison de s'inquiéter.