Baccalauréat série S Amérique du Sud 17 novembre 2014 - Exercice 4
Exercice 4 5 points
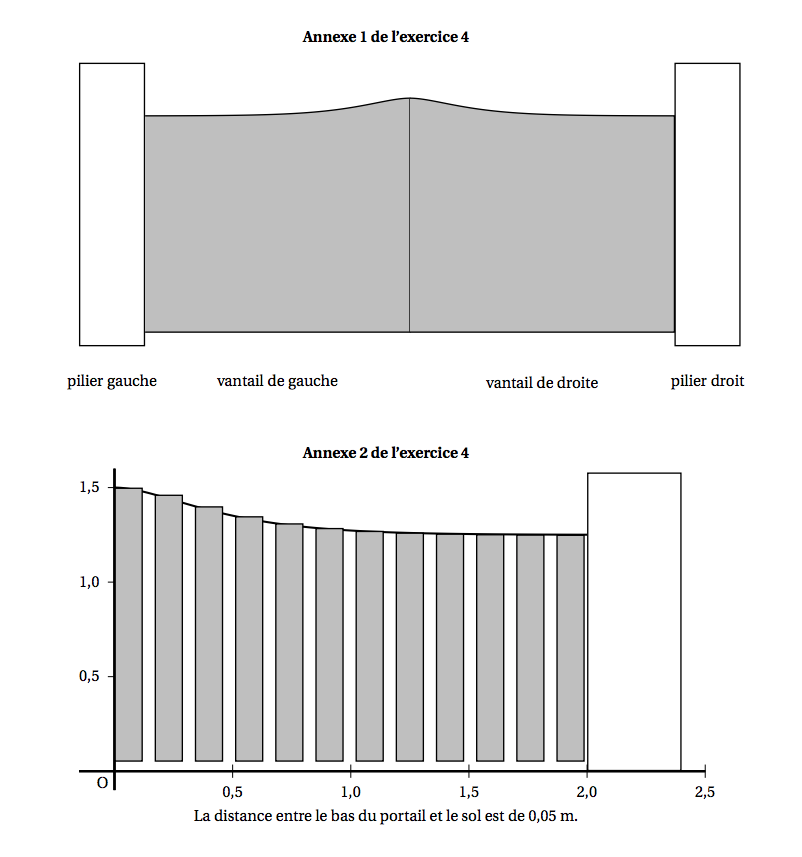
On désire réaliser un portail comme indiqué à l'annexe 1. Chaque vantail mesure 2 mètres de large.
Partie A : modélisation de la partie supérieure du portail
On modélise le bord supérieur du vantail de droite du portail avec une fonction $f$ définie sur l'intervalle [0 ; 2] par \[f(x) = \left(x + \dfrac{1}{4}\right)\text{e}^{- 4x} + b\] où $b$ est un nombre réel. On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle [0 ; 2].
-
- Calculer $f'(x)$, pour tout réel $x$ appartenant à l'intervalle [0 ; 2].
- En déduire le sens de variation de la fonction $f$ sur l'intervalle [0 ; 2].
- Déterminer le nombre $b$ pour que la hauteur maximale du portail soit égale à 1,5 m.
Dans la suite la fonction $f$ est définie sur l'intervalle [0 ; 2] par \[f(x) = \left(x + \dfrac{1}{4}\right)\text{e}^{- 4x} + \dfrac{5}{4}.\]
Partie B : détermination d'une aire
Chaque vantail est réalisé à l'aide d'une plaque métallique. On veut calculer l'aire de chacune des plaques, sachant que le bord inférieur du vantail est à 0,05 m de hauteur du sol.
- Montrer que la fonction $F$ définie sur l'intervalle [0 ; 2] par \[F(x) = \left(- \dfrac{x}{4} - \dfrac{1}{8}\right)\text{e}^{-4x} + \dfrac{5}{4}x\] est une primitive de la fonction $f$.
- En déduire l'aire en m$^2$ de chaque vantail. On donnera la valeur exacte puis une valeur approchée à $10^{- 2}$ près de cette aire. (On s'intéresse ici à l'objet « vantail» sans faire référence à son environnement).
Partie C : utilisation d'un algorithme
On désire réaliser un portail de m ême forme mais à partir de planches rectangulaires disjointes de largeur 0,12 m, espacées de 0,05 m. Pour le vantail de droite, le coin supérieur gauche de chaque planche est situé sur le bord supérieur du vantail (voir l'annexe 2 de l'exercice 4) et le bas de chaque planche à 0,05 m de hauteur. Les planches sont numérotées à partir de $0$ : ainsi la première planche à gauche porte le numéro $0$.
- Donner l'aire de la planche numéro $k$.
- Recopier et compléter l'algorithme suivant pour qu'il calcule la somme des aires des planches du vantail de droite. $$\begin{array}{ |l l|}\hline \text{ Variables :}& \text{ Les nombres } X \text{ et } S \text{ sont des nombres réels}\\ \text{Initialisation:} & \text{ On affecte à } S \text{ la valeur 0} \\ &\text{ On affecte à } X \text{ la valeur 0}\\ \text{ Traitement :}& \text{Tant Que} X + 0,17 < \ldots\\ & \hspace{1cm}S \text{ prend la valeur } S + \ldots.\\ &\hspace{1cm} X \text{ prend la valeur } X + 0,17\\ &\text{Fin de Tant Que}\\ \text{ Affichage :}& \text{ On affiche } S\\ \hline \end{array}$$
- Vues: 37528
