Baccalauréat série S Amérique du Sud 17 novembre 2014 - Correction Exercice 1
Correction de l'exercice 1 (6 points)
Une entreprise est spécialisée dans la fabrication de ballons de football. Cette entreprise propose deux tailles de ballons :
- une petite taille,
- une taille standard.
Les trois parties suivantes sont indépendantes.
Partie A
Un ballon de football est conforme à la réglementation s'il respecte, suivant sa taille, deux conditions à la fois (sur sa masse et sur sa circonférence).
En particulier, un ballon de taille standard est conforme à la réglementation lorsque sa masse, exprimée en grammes, appartient à l'intervalle [410 ; 450] et sa circonférence, exprimée en centimètres, appartient à l'intervalle [68 ; 70].
- On note $X$ la variable aléatoire qui, à chaque ballon de taille standard choisi au hasard dans l'entreprise, associe sa masse en grammes. On admet que $X$ suit la loi normale d'espérance 430 et d'écart type 10. Déterminer une valeur approchée à $10^{-3}$ près de la probabilité $P(410 \leqslant X \leqslant 450)$. $P(410 \le X \le 450) = P(\mu – 2\sigma \le X \le \mu + 2\sigma)$ $\approx 0,954$
- On note $Y$ la variable aléatoire qui, à chaque ballon de taille standard choisi au hasard dans l'entreprise associe sa circonférence en centimètres. On admet que $Y$ suit la loi normale d'espérance 69 et d'écart type $\sigma$. Déterminer la valeur de $\sigma$, au centième près, sachant que 97$\,\%$ des ballons de taille standard ont une circonférence conforme à la réglementation. On pourra utiliser le résultat suivant: lorsque $Z$ est une variable aléatoire qui suit la loi normale centrée réduite, alors $P(- \beta \leqslant Z \leqslant \beta) = 0,97$ pour $\beta \approx 2,17$. On cherche donc :
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$\begin{array} {ll}P(68 \le Y \le 70) = 0,97 & \Leftrightarrow P(68 – 69 \le Y – 69 \le 70 – 69) = 0,97 \\ & \Leftrightarrow P\left(\dfrac{-1}{\sigma}\le \dfrac{Y – 69}{\sigma} \le \dfrac{1}{\sigma} \right) = 0,97 \end{array}$$ La variable aléatoire $\dfrac{Y – 69}{\sigma}$ suit donc la loi normale centrée réduite.
On a ainsi : $ \dfrac{1}{\sigma} \approx 2,17 \Leftrightarrow \sigma \approx \dfrac{1}{2,17} \Leftrightarrow \sigma \approx 0,46$
Partie B
On a $n = 250$ et $p=0,98$.
On a donc $n = 250 \ge 30$, $np = 245 \ge 5$ et $n(1-p) = 5 \ge 5$.
Les conditions sont donc vérifiées pour déterminer l’intervalle de fluctuation au seuil de $95\%$.
On a ainsi :
$$\begin{array}{ll} I_{250} & = \left[0,98 – 1,96 \sqrt{\dfrac{0,98\times 0,02}{250}};\dfrac{233}{250} + 1,96 \sqrt{\dfrac{0,98 \times 0,02}{250}}\right]\\ & \approx [0,962;0,998] \end{array}$$ La fréquence observée est $f = \dfrac{233}{250} = 0,932 \notin I_{250}$. Cela signifie donc, qu’au risque de $5\%$, l’affirmation de l’entreprise est remise en question.
Partie C
L'entreprise produit 40$\,\%$ de ballons de football de petite taille et 60$\,\%$ de ballons de taille standard. On admet que 2$\,\%$ des ballons de petite taille et 5$\,\%$ des ballons de taille standard ne sont pas conformes à la réglementation. On choisit un ballon au hasard dans l'entreprise. On considère les évènements : $A$ : « le ballon de football est de petite taille », $B$ : « le ballon de football est de taille standard », $C$ : « le ballon de football est conforme à la réglementation» et $\overline{C}$, l'évènement contraire de $C$.
- Représenter cette expérience aléatoire à l'aide d'un arbre de probabilité.
- Calculer la probabilité que le ballon de football soit de petite taille et soit conforme à la règlementation. On cherche donc $p(A \cap C) = 0,4 \times 0,98 = 0,392$
- Montrer que la probabilité de l'évènement $C$ est égale à $0,962$. D’après la formule des probabilités totales, on a :
- Le ballon de football choisi n'est pas conforme à la réglementation. Quelle est la probabilité que ce ballon soit de petite taille ? On arrondira le résultat à $10^{- 3}$. On cherche ici à calculer $p_{\overline{C}}(A) = \dfrac{p\left(\overline{C} \cap A\right)}{p\left(\overline{C}\right)} = \dfrac{0,4 \times 0,02}{1 – 0,962}$ $\approx 0,211$.
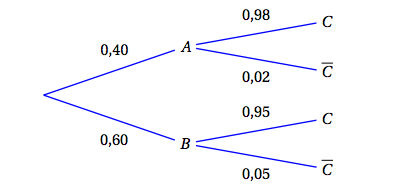
$$\begin{array} {ll}p(C) & = p(A \cap C) + p(B \cap C) \\ & = 0,392 + 0,6 \times 0,95 \\ &= 0,962 \end{array}$$
- Vues: 37467
