Baccalauréat série S Amérique du Sud 17 novembre 2014
Exercice 1 6 points
Une entreprise est spécialisée dans la fabrication de ballons de football. Cette entreprise propose deux tailles de ballons :
- une petite taille,
- une taille standard.
Les trois parties suivantes sont indépendantes.
Partie A
Un ballon de football est conforme à la réglementation s'il respecte, suivant sa taille, deux conditions à la fois (sur sa masse et sur sa circonférence).
En particulier, un ballon de taille standard est conforme à la réglementation lorsque sa masse, exprimée en grammes, appartient à l'intervalle [410 ; 450] et sa circonférence, exprimée en centimètres, appartient à l'intervalle [68 ; 70].
- On note $X$ la variable aléatoire qui, à chaque ballon de taille standard choisi au hasard dans l'entreprise, associe sa masse en grammes. On admet que $X$ suit la loi normale d'espérance 430 et d'écart type 10. Déterminer une valeur approchée à $10^{-3}$ près de la probabilité $P(410 \leqslant X \leqslant 450)$.
- On note $Y$ la variable aléatoire qui, à chaque ballon de taille standard choisi au hasard dans l'entreprise associe sa circonférence en centimètres. On admet que $Y$ suit la loi normale d'espérance 69 et d'écart type $\sigma$. Déterminer la valeur de $\sigma$, au centième près, sachant que 97$\,\%$ des ballons de taille standard ont une circonférence conforme à la réglementation. On pourra utiliser le résultat suivant: lorsque $Z$ est une variable aléatoire qui suit la loi normale centrée réduite, alors $P(- \beta \leqslant Z \leqslant \beta) = 0,97$ pour $\beta \approx 2,17$.
Partie B
L'entreprise affirme que 98$\,\%$ de ses ballons de taille standard sont conformes à la réglementation. Un contrôle est alors réalisé sur un échantillon de 250 ballons de taille standard. Il est constaté que 233 d'entre eux sont conformes à la réglementation. Le résultat de ce contrôle remet-il en question l'affirmation de l'entreprise ? Justifier la réponse. (On pourra utiliser l'intervalle de fluctuation)
Partie C
L'entreprise produit 40$\,\%$ de ballons de football de petite taille et 60$\,\%$ de ballons de taille standard. On admet que 2$\,\%$ des ballons de petite taille et 5$\,\%$ des ballons de taille standard ne sont pas conformes à la réglementation. On choisit un ballon au hasard dans l'entreprise. On considère les évènements : $A$ : « le ballon de football est de petite taille », $B$ : « le ballon de football est de taille standard », $C$ : « le ballon de football est conforme à la réglementation» et $\overline{C}$, l'évènement contraire de $C$.
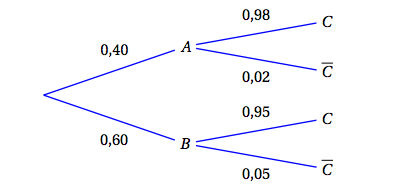
- Représenter cette expérience aléatoire à l'aide d'un arbre de probabilité.
- Calculer la probabilité que le ballon de football soit de petite taille et soit conforme à la règlementation.
- Montrer que la probabilité de l'évènement $C$ est égale à $0,962$.
- Le ballon de football choisi n'est pas conforme à la réglementation. Quelle est la probabilité que ce ballon soit de petite taille ? On arrondira le résultat à $10^{- 3}$.
Correction de l'exercice 1 (6 points)
Une entreprise est spécialisée dans la fabrication de ballons de football. Cette entreprise propose deux tailles de ballons :
- une petite taille,
- une taille standard.
Les trois parties suivantes sont indépendantes.
Partie A
Un ballon de football est conforme à la réglementation s'il respecte, suivant sa taille, deux conditions à la fois (sur sa masse et sur sa circonférence).
En particulier, un ballon de taille standard est conforme à la réglementation lorsque sa masse, exprimée en grammes, appartient à l'intervalle [410 ; 450] et sa circonférence, exprimée en centimètres, appartient à l'intervalle [68 ; 70].
- On note $X$ la variable aléatoire qui, à chaque ballon de taille standard choisi au hasard dans l'entreprise, associe sa masse en grammes. On admet que $X$ suit la loi normale d'espérance 430 et d'écart type 10. Déterminer une valeur approchée à $10^{-3}$ près de la probabilité $P(410 \leqslant X \leqslant 450)$. $P(410 \le X \le 450) = P(\mu – 2\sigma \le X \le \mu + 2\sigma)$ $\approx 0,954$
- On note $Y$ la variable aléatoire qui, à chaque ballon de taille standard choisi au hasard dans l'entreprise associe sa circonférence en centimètres. On admet que $Y$ suit la loi normale d'espérance 69 et d'écart type $\sigma$. Déterminer la valeur de $\sigma$, au centième près, sachant que 97$\,\%$ des ballons de taille standard ont une circonférence conforme à la réglementation. On pourra utiliser le résultat suivant: lorsque $Z$ est une variable aléatoire qui suit la loi normale centrée réduite, alors $P(- \beta \leqslant Z \leqslant \beta) = 0,97$ pour $\beta \approx 2,17$. On cherche donc :
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$\begin{array} {ll}P(68 \le Y \le 70) = 0,97 & \Leftrightarrow P(68 – 69 \le Y – 69 \le 70 – 69) = 0,97 \\ & \Leftrightarrow P\left(\dfrac{-1}{\sigma}\le \dfrac{Y – 69}{\sigma} \le \dfrac{1}{\sigma} \right) = 0,97 \end{array}$$ La variable aléatoire $\dfrac{Y – 69}{\sigma}$ suit donc la loi normale centrée réduite.
On a ainsi : $ \dfrac{1}{\sigma} \approx 2,17 \Leftrightarrow \sigma \approx \dfrac{1}{2,17} \Leftrightarrow \sigma \approx 0,46$
Partie B
On a $n = 250$ et $p=0,98$.
On a donc $n = 250 \ge 30$, $np = 245 \ge 5$ et $n(1-p) = 5 \ge 5$.
Les conditions sont donc vérifiées pour déterminer l’intervalle de fluctuation au seuil de $95\%$.
On a ainsi :
$$\begin{array}{ll} I_{250} & = \left[0,98 – 1,96 \sqrt{\dfrac{0,98\times 0,02}{250}};\dfrac{233}{250} + 1,96 \sqrt{\dfrac{0,98 \times 0,02}{250}}\right]\\ & \approx [0,962;0,998] \end{array}$$ La fréquence observée est $f = \dfrac{233}{250} = 0,932 \notin I_{250}$. Cela signifie donc, qu’au risque de $5\%$, l’affirmation de l’entreprise est remise en question.
Partie C
L'entreprise produit 40$\,\%$ de ballons de football de petite taille et 60$\,\%$ de ballons de taille standard. On admet que 2$\,\%$ des ballons de petite taille et 5$\,\%$ des ballons de taille standard ne sont pas conformes à la réglementation. On choisit un ballon au hasard dans l'entreprise. On considère les évènements : $A$ : « le ballon de football est de petite taille », $B$ : « le ballon de football est de taille standard », $C$ : « le ballon de football est conforme à la réglementation» et $\overline{C}$, l'évènement contraire de $C$.
- Représenter cette expérience aléatoire à l'aide d'un arbre de probabilité.
- Calculer la probabilité que le ballon de football soit de petite taille et soit conforme à la règlementation. On cherche donc $p(A \cap C) = 0,4 \times 0,98 = 0,392$
- Montrer que la probabilité de l'évènement $C$ est égale à $0,962$. D’après la formule des probabilités totales, on a :
- Le ballon de football choisi n'est pas conforme à la réglementation. Quelle est la probabilité que ce ballon soit de petite taille ? On arrondira le résultat à $10^{- 3}$. On cherche ici à calculer $p_{\overline{C}}(A) = \dfrac{p\left(\overline{C} \cap A\right)}{p\left(\overline{C}\right)} = \dfrac{0,4 \times 0,02}{1 – 0,962}$ $\approx 0,211$.
$$\begin{array} {ll}p(C) & = p(A \cap C) + p(B \cap C) \\ & = 0,392 + 0,6 \times 0,95 \\ &= 0,962 \end{array}$$
Exercice 2 4 points
Cet exercice est un questionnaire à choix multiples. Aucune justification n'est demandée. Pour chacune des questions, une seule des quatre propositions est correcte. Chaque réponse correcte rapporte un point. Une réponse erronée ou une absence de réponse n'enlève pas de point. On notera sur la copie le numéro de la question suivi de la lettre correspondant à la proposition choisie.
- Dans un repère orthonormé de l'espace, on considère les points A$(2 ; 5 ; - 1)$, B$(3 ; 2 ; 1)$ et C$(1 ; 3 ; - 2)$. Le triangle ABC est :
- rectangle et non isocèle
- isocèle et non rectangle
- rectangle et isocèle
- équilatéral
- Dans un repère orthonormé de l'espace, on considère le plan $P$ d'équation $2x - y + 3z - 1 = 0$ et le point A$(2 ; 5 ; -1)$. Une représentation paramétrique de la droite $d$, perpendiculaire au plan $P$ et passant par A est :
$$\begin{array}{lll} \text{a. }\left\{\begin{array}{l c l} x &=& 2 + 2t\\ y &=& 5+t\\ z &=& - 1 + 3t \end{array}\right.& \text{ b. }\left\{\begin{array}{l c l} x &=& 2 + 2t\\ y &=& - 1 + 5t\\ z &=& 3 - t \end{array}\right.& \text{ c. }\left\{\begin{array}{l c l} x &=& 6 - 2t\\ y &=& 3 + t\\ z &=& 5 - 3t \end{array}\right.& \text{ d. }\left\{\begin{array}{l c l} x &=& 1 + 2t \\ y &=& 4 - t\\ z &=& - 2 + 3t \end{array}\right.\\ \end{array}$$ - Soit A et B deux points distincts du plan. L'ensemble des points $M$ du plan tels que $\vec{M\text{A}} \cdot \vec{M\text{B}} = 0$ est :
\begin{array}{llll} \text{a. }\text{l'ensemble vide}& \text{ b. } \text{la médiatrice du segment} [AB] &\text{ c. } \text{le cercle de diamètre }[AB] &\text{ d. } \text{ la droite } (AB) \end{array} - La figure ci-dessous représente un cube ABCDEFGH. Les points I et J sont les milieux respectifs des arêtes [GH] et [FG]. Les points M et N sont les centres respectifs des faces ABFE et BCGF.
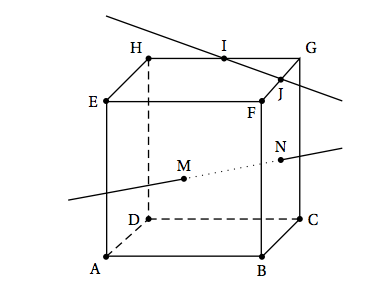
Les droites (IJ) et (MN) sont :- perpendiculaires
- sécantes, non perpendiculaires
- orthogonales
- parallèles
Correction de l'exercice 2 (5 points)
Cet exercice est un questionnaire à choix multiples. Aucune justification n'est demandée. Pour chacune des questions, une seule des quatre propositions est correcte. Chaque réponse correcte rapporte un point. Une réponse erronée ou une absence de réponse n'enlève pas de point. On notera sur la copie le numéro de la question suivi de la lettre correspondant à la proposition choisie.
- Dans un repère orthonormé de l'espace, on considère les points A$(2 ; 5 ; - 1)$, B$(3 ; 2 ; 1)$ et C$(1 ; 3 ; - 2)$. Le triangle ABC est :
- rectangle et non isocèle
- isocèle et non rectangle
- rectangle et isocèle
- équilatéral
Déterminons les coordonnées des différents vecteurs. - Dans un repère orthonormé de l'espace, on considère le plan $P$ d'équation $2x - y + 3z - 1 = 0$ et le point A$(2 ; 5 ; -1)$. Une représentation paramétrique de la droite $d$, perpendiculaire au plan $P$ et passant par A est :
$$\begin{array}{lll} \text{a. }\left\{\begin{array}{l c l} x &=& 2 + 2t\\ y &=& 5+t\\ z &=& - 1 + 3t \end{array}\right.& \text{ b. }\left\{\begin{array}{l c l} x &=& 2 + 2t\\ y &=& - 1 + 5t\\ z &=& 3 - t \end{array}\right.& \text{ c. }\left\{\begin{array}{l c l} x &=& 6 - 2t\\ y &=& 3 + t\\ z &=& 5 - 3t \end{array}\right.& \text{ d. }\left\{\begin{array}{l c l} x &=& 1 + 2t \\ y &=& 4 - t\\ z &=& - 2 + 3t \end{array}\right.\\ \end{array}$$ Un vecteur normal est $\vec{n}(2;-1;3)$. Ce vecteur est donc un vecteur directeur de $d$. - Soit A et B deux points distincts du plan. L'ensemble des points $M$ du plan tels que $\vec{M\text{A}} \cdot \vec{M\text{B}} = 0$ est :
\begin{array}{llll} \text{a. }\text{l'ensemble vide}& \text{ b. } \text{la médiatrice du segment} [AB] &\text{ c. } \text{le cercle de diamètre }[AB] &\text{ d. } \text{ la droite } (AB) \end{array} $\vec{MA}.\vec{MB} = 0 \Leftrightarrow AMB$ rectangle en $M$ $\Leftrightarrow$ $M$ appartient au cercle de diamètre $[AB]$ - La figure ci-dessous représente un cube ABCDEFGH. Les points I et J sont les milieux respectifs des arêtes [GH] et [FG]. Les points M et N sont les centres respectifs des faces ABFE et BCGF.

Les droites (IJ) et (MN) sont :- perpendiculaires
- sécantes, non perpendiculaires
- orthogonales
- parallèles
Les points $M$ et $N$ appartiennent tous les deux à un plan parallèle au plan $EFG$, auquel appartient la droite $(IJ)$. Ce ne peut donc pas êtres les réponses a et b.
$\vec{AB}(1;-3;2)$ $\quad$ $\vec{AC}(-1;-2;-1)$ $\quad$ $\vec{BC}(-2;1;-3)$
Donc $AB^2 = 1 + 9 + 4 = 14$ $\quad$ $AC^2 = 1 + 2 + 1 = 4$ et $BC^2 = 4 + 1 +9 = 14$
On constate donc que $AB = BC$ mais $AC^2 \neq AB^2 + BC^2$. D’après la contraposée du théorème de Pythagore, le triangle ABC n’est pas rectangle.
Réponse B
Par conséquent, seules les propositions c et d peuvent convenir.
Cette droite doit passer par le point $A(2;5;-1)$.
Si on considère la représentation paramétrique c, en prenant $t= 2$ alors : $\begin{cases} x = 6 – 4 = 2 \\\\y = 3 + 2 = 5\\\\z= 5 – 6 = -1 \end{cases}$.
Par conséquent la bonne réponse est la réponse C$\quad$
Réponse C
La droite parallèle à $(MN)$ passant par $J$ coupe $[EF]$ en son milieu. Par conséquent cette droite et $(IJ)$, qui appartiennent toutes les deux au plan $EFG$ ne sont pas parallèles.
Réponse C
Exercice 3 5 points
On considère la suite numérique $\left(u_n\right)$ définie sur $\mathbb N$ par : \[u_0 = 2 \quad \text{et pour tout entier naturel } n, \quad u_{n+1} = - \dfrac{1}{2}u_n^2 + 3u_n - \dfrac{3}{2}.\]
Partie A : Conjecture
- Calculer les valeurs exactes, données en fractions irréductibles, de $u_1$ et $u_2$.
- Donner une valeur approchée à $10^{-5}$ près des termes $u_3$ et $u_4$.
- Conjecturer le sens de variation et la convergence de la suite $\left(u_n\right)$.
Partie B: Validation des conjectures
On considère la suite numérique $\left(v_n\right)$ définie pour tout entier naturel $n$, par : $v_n = u_n - 3$.
- Montrer que, pour tout entier naturel $n,\: v_{n+1} = - \dfrac{1}{2}v_n^2$.
- Démontrer par récurrence que, pour tout entier naturel $n,\: -1 \leqslant v_n \leqslant 0$.
-
- Démontrer que, pour tout entier naturel $n,\: v_{n+1} - v_n = -v_n\left(\dfrac{1}{2}v_n + 1\right)$.
- En déduire le sens de variation de la suite $\left(v_n\right)$.
- Pourquoi peut-on alors affirmer que la suite $\left(v_n\right)$ converge ?
- On note $\ell$ la limite de la suite $\left(v_n\right)$. On admet que $\ell$ appartient à l'intervalle $[- 1 ; 0]$ et vérifie l'égalité : $\ell = - \dfrac{1}{2}\ell^2$. Déterminer la valeur de $\ell$.
- Les conjectures faites dans la partie A sont-elles validées ?
Correction de l'exercice 3 (5 points)
On considère la suite numérique $\left(u_n\right)$ définie sur $\mathbb N$ par : \[u_0 = 2 \quad \text{et pour tout entier naturel } n, \quad u_{n+1} = - \dfrac{1}{2}u_n^2 + 3u_n - \dfrac{3}{2}.\]
Partie A : Conjecture
- Calculer les valeurs exactes, données en fractions irréductibles, de $u_1$ et $u_2$. $u_1 = -\dfrac{1}{2} \times 2^2 + 3 \times 2 – \dfrac{3}{2} = \dfrac{5}{2}$
- Donner une valeur approchée à $10^{-5}$ près des termes $u_3$ et $u_4$. On a ensuite $u_3 \approx 2,99219$ et $u_4 \approx 2,99997$
- Conjecturer le sens de variation et la convergence de la suite $\left(u_n\right)$. Il semblerait donc que la suite $(u_n)$ soit croissante et converge vers $3$.
$\quad$
$u_2 = – \dfrac{1}{2} \times \left(\dfrac{5}{2}\right)^2 + 3 \times \dfrac{5}{2} – \dfrac{3}{2} = \dfrac{23}{8}$
Partie B: Validation des conjectures
On considère la suite numérique $\left(v_n\right)$ définie pour tout entier naturel $n$, par : $v_n = u_n - 3$.
- Montrer que, pour tout entier naturel $n,\: v_{n+1} = - \dfrac{1}{2}v_n^2$. $$\begin{array}{ll} v_{n+1} &= u_{n+1} – 3 \\ &= -\dfrac{1}{2} u_n^2 + 3u_n – \dfrac{3}{2} – 3 \\ &= -\dfrac{1}{2} u_n^2 + 3u_n – \dfrac{9}{2} \\ &= – \dfrac{1}{2} \left(u_n^2 – 6u_n + 9\right) \\ &= -\dfrac{1}{2} (u_n – 3)^2 \\ &= – \dfrac{1}{2} v_n^2 \end{array}$$
- Démontrer par récurrence que, pour tout entier naturel $n,\: -1 \leqslant v_n \leqslant 0$. Initialisation : Si $n = 0$ alors $v_0 = 2 – 3 = -1$ donc $-1 \le v_0 \le 0$.
-
- Démontrer que, pour tout entier naturel $n,\: v_{n+1} - v_n = -v_n\left(\dfrac{1}{2}v_n + 1\right)$. $v_{n+1} – v_n = -\dfrac{1}{2}v_n^2 – v_n = -v_n \left(-\dfrac{1}{2}v_n + 1\right)$
- En déduire le sens de variation de la suite $\left(v_n\right)$. On sait que $-1 \le v_n \le 0$ donc $-v_n \ge 0$
De plus $-\dfrac{1}{2} \le \dfrac{1}{2} v_n \le 0$ soit $\dfrac{1}{2} \le \dfrac{1}{2} v_n + 1 \le 1$. Par conséquent $\dfrac{1}{2} v_n + 1 \ge 0$
Finalement, $v_{n+1}-v_n \ge 0$.
La suite $(v_n)$ est donc croissante. - Pourquoi peut-on alors affirmer que la suite $\left(v_n\right)$ converge ? La suite $(v_n)$ est croissante et majorée par $0$. Elle converge donc.
- On note $\ell$ la limite de la suite $\left(v_n\right)$. On admet que $\ell$ appartient à l'intervalle $[- 1 ; 0]$ et vérifie l'égalité : $\ell = - \dfrac{1}{2}\ell^2$. Déterminer la valeur de $\ell$. $l = -\dfrac{1}{2}l^2 \Leftrightarrow l + \dfrac{1}{2}l^2 = 0 \Leftrightarrow l \left(1 + \dfrac{1}{2}l \right) = 0$
- Les conjectures faites dans la partie A sont-elles validées ? On sait que :
La propriété est donc vraie au rang $0$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $-1 \le v_n \le 0$.
Ainsi $ 0 \le v_n^2 \le 1$ et $-\dfrac{1}{2} \le -\dfrac{1}{2}v_n^2 \le 0$ soit $-1 \le v_{n+1} \le 0$.
La propriété est donc vraie au rang $n+1$
$\quad$
Conclusion : La propriété est vraie au rang $0$. Si la propriété est vraie au rang $n$ alors elle est également vraie au rang suivant.
Par conséquent, pour tout entier naturel $n$, on a $-1 \le v_n \le 0$.
Cela signifie donc que $l = 0$ ou $1 + \dfrac{1}{2}l = 0$ (et donc $l=-2$).
On sait que $l \in [-1;0]$. Par conséquent $l = 0$.
– la suite $(v_n)$ est croissante et converge vers $0$
– $u_n = v_n + 3$
Par conséquent la suite $(u_n)$ est également croissante et converge vers $3$.
Les conjectures de la partie A sont donc validées.
Exercice 4 5 points
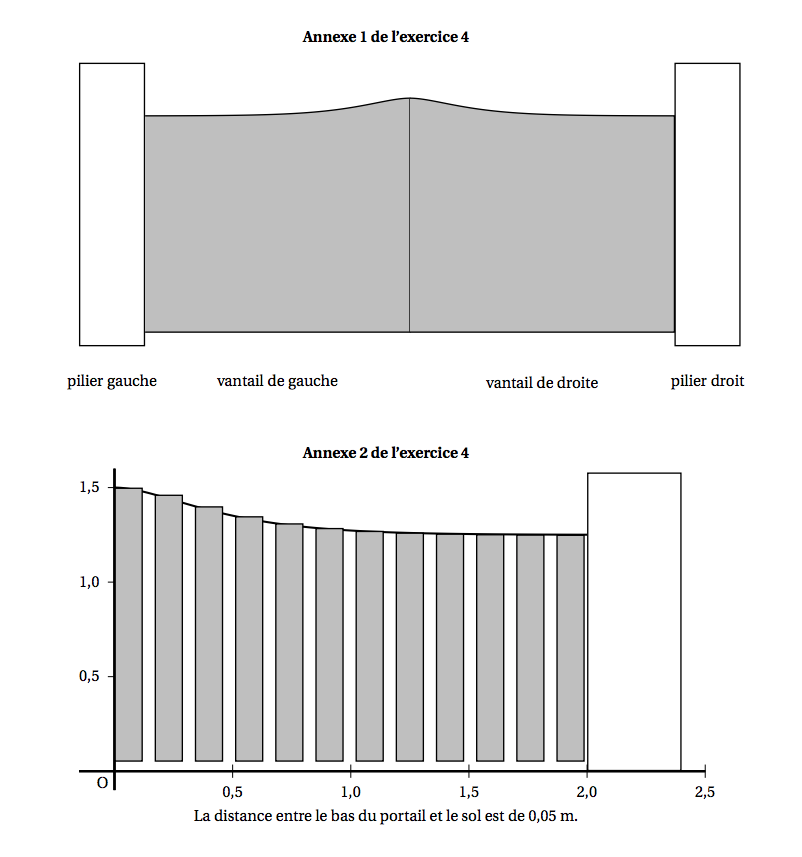
On désire réaliser un portail comme indiqué à l'annexe 1. Chaque vantail mesure 2 mètres de large.
Partie A : modélisation de la partie supérieure du portail
On modélise le bord supérieur du vantail de droite du portail avec une fonction $f$ définie sur l'intervalle [0 ; 2] par \[f(x) = \left(x + \dfrac{1}{4}\right)\text{e}^{- 4x} + b\] où $b$ est un nombre réel. On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle [0 ; 2].
-
- Calculer $f'(x)$, pour tout réel $x$ appartenant à l'intervalle [0 ; 2].
- En déduire le sens de variation de la fonction $f$ sur l'intervalle [0 ; 2].
- Déterminer le nombre $b$ pour que la hauteur maximale du portail soit égale à 1,5 m.
Dans la suite la fonction $f$ est définie sur l'intervalle [0 ; 2] par \[f(x) = \left(x + \dfrac{1}{4}\right)\text{e}^{- 4x} + \dfrac{5}{4}.\]
Partie B : détermination d'une aire
Chaque vantail est réalisé à l'aide d'une plaque métallique. On veut calculer l'aire de chacune des plaques, sachant que le bord inférieur du vantail est à 0,05 m de hauteur du sol.
- Montrer que la fonction $F$ définie sur l'intervalle [0 ; 2] par \[F(x) = \left(- \dfrac{x}{4} - \dfrac{1}{8}\right)\text{e}^{-4x} + \dfrac{5}{4}x\] est une primitive de la fonction $f$.
- En déduire l'aire en m$^2$ de chaque vantail. On donnera la valeur exacte puis une valeur approchée à $10^{- 2}$ près de cette aire. (On s'intéresse ici à l'objet « vantail» sans faire référence à son environnement).
Partie C : utilisation d'un algorithme
On désire réaliser un portail de m ême forme mais à partir de planches rectangulaires disjointes de largeur 0,12 m, espacées de 0,05 m. Pour le vantail de droite, le coin supérieur gauche de chaque planche est situé sur le bord supérieur du vantail (voir l'annexe 2 de l'exercice 4) et le bas de chaque planche à 0,05 m de hauteur. Les planches sont numérotées à partir de $0$ : ainsi la première planche à gauche porte le numéro $0$.
- Donner l'aire de la planche numéro $k$.
- Recopier et compléter l'algorithme suivant pour qu'il calcule la somme des aires des planches du vantail de droite. $$\begin{array}{ |l l|}\hline \text{ Variables :}& \text{ Les nombres } X \text{ et } S \text{ sont des nombres réels}\\ \text{Initialisation:} & \text{ On affecte à } S \text{ la valeur 0} \\ &\text{ On affecte à } X \text{ la valeur 0}\\ \text{ Traitement :}& \text{Tant Que} X + 0,17 < \ldots\\ & \hspace{1cm}S \text{ prend la valeur } S + \ldots.\\ &\hspace{1cm} X \text{ prend la valeur } X + 0,17\\ &\text{Fin de Tant Que}\\ \text{ Affichage :}& \text{ On affiche } S\\ \hline \end{array}$$
Correction de l'exercice 4 5 points
On désire réaliser un portail comme indiqué à l'annexe 1. Chaque vantail mesure 2 mètres de large.
Partie A : modélisation de la partie supérieure du portail
On modélise le bord supérieur du vantail de droite du portail avec une fonction $f$ définie sur l'intervalle [0 ; 2] par \[f(x) = \left(x + \dfrac{1}{4}\right)\text{e}^{- 4x} + b\] où $b$ est un nombre réel. On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle [0 ; 2].
-
- Calculer $f'(x)$, pour tout réel $x$ appartenant à l'intervalle [0 ; 2]. $f$ est dérivable sur $[0;2]$ en tant que produit de fonctions dérivables sur cet intervalle.
- En déduire le sens de variation de la fonction $f$ sur l'intervalle [0 ; 2]. Sur l’intervalle $[0;2]$ $-4x \le 0$ et $\text{e}^{-4x} > 0$.
$f'(x) = \text{e}^{-4x} + \left(x + \dfrac{1}{4} \right) \times (-4) \text{e}^{-4x} = \text{-4x} + (-4x – 1)\text{e}^{-4x} $ $=(1 – 4x – 1)\text{e}^{-4x}$ $=-4x \text{e}^{-4x}$
Par conséquent $f'(x) \le 0$ sur [$0;2]$ et la fonction $f$ est décroissante sur $[0;2]$. - Déterminer le nombre $b$ pour que la hauteur maximale du portail soit égale à 1,5 m. La fonction $f$ atteint donc son maximum en $0$ sur $[0;2]$
Or $f(0) = \dfrac{1}{4} + b$.
On veut donc que $\dfrac{1}{4} + b = \dfrac{3}{2}$ soit $b = \dfrac{3}{2} – \dfrac{1}{4} = \dfrac{5}{4}$.
Dans la suite la fonction $f$ est définie sur l'intervalle [0 ; 2] par \[f(x) = \left(x + \dfrac{1}{4}\right)\text{e}^{- 4x} + \dfrac{5}{4}.\]
Partie B : détermination d'une aire
Chaque vantail est réalisé à l'aide d'une plaque métallique. On veut calculer l'aire de chacune des plaques, sachant que le bord inférieur du vantail est à 0,05 m de hauteur du sol.
- Montrer que la fonction $F$ définie sur l'intervalle [0 ; 2] par \[F(x) = \left(- \dfrac{x}{4} - \dfrac{1}{8}\right)\text{e}^{-4x} + \dfrac{5}{4}x\] est une primitive de la fonction $f$. La fonction $F$ est dérivable sur $[0;2]$ en tant que somme et produit de fonctions dérivables sur cet intervalle.
- En déduire l'aire en m$^2$ de chaque vantail. On donnera la valeur exacte puis une valeur approchée à $10^{- 2}$ près de cette aire. (On s'intéresse ici à l'objet « vantail» sans faire référence à son environnement). L’aire de chaque vantail est donc donnée par :
$$\begin{array} {ll}F'(x) &= -\dfrac{1}{4}\text{e}^{-4x} – 4\left(-\dfrac{x}{4} – \dfrac{1}{8}\right)\text{e}^{-4x} + \dfrac{5}{4} \\ &= \left(-\dfrac{1}{4} + x + \dfrac{1}{2}\right)\text{e}^{-4x} + \dfrac{5}{4} \\ &= \left(x + \dfrac{1}{4}\right)\text{e}^{-4x} + \dfrac{5}{4} \\ &= f(x) \end{array}$$
Par conséquent la fonction $F$ est bien une primitive de la fonction $f$ sur $[0;2]$.
$\mathscr{A} = \displaystyle \int_0^2 f(x) \text{d}x = F(2) – F(0)$
Or $F(2) = -\dfrac{5}{8}\text{e}^{-8} + \dfrac{5}{2}$ et $F(0) = -\dfrac{1}{8}$
Donc $\mathscr{A} = \dfrac{21}{8} – \dfrac{5}{8}\text{e}^{-8} \approx 2,62 \text{ m}^2$.
Partie C : utilisation d'un algorithme
On désire réaliser un portail de m ême forme mais à partir de planches rectangulaires disjointes de largeur 0,12 m, espacées de 0,05 m. Pour le vantail de droite, le coin supérieur gauche de chaque planche est situé sur le bord supérieur du vantail (voir l'annexe 2 de l'exercice 4) et le bas de chaque planche à 0,05 m de hauteur. Les planches sont numérotées à partir de $0$ : ainsi la première planche à gauche porte le numéro $0$.
- Donner l'aire de la planche numéro $k$. On considère la planche numéro $k$.
- Recopier et compléter l'algorithme suivant pour qu'il calcule la somme des aires des planches du vantail de droite. $$\begin{array}{ |l l|}\hline \text{ Variables :}& \text{ Les nombres } X \text{ et } S \text{ sont des nombres réels}\\ \text{Initialisation:} & \text{ On affecte à } S \text{ la valeur 0} \\ &\text{ On affecte à } X \text{ la valeur 0}\\ \text{ Traitement :}& \text{Tant Que} X + 0,17 < \ldots\\ & \hspace{1cm}S \text{ prend la valeur } S + \ldots.\\ &\hspace{1cm} X \text{ prend la valeur } X + 0,17\\ &\text{Fin de Tant Que}\\ \text{ Affichage :}& \text{ On affiche } S\\ \hline \end{array}$$
 Variables :
Variables :
Sa largeur est : $ 0,12$
Sa longueur est :
$$\begin{array}{ll} f\left((0,05+0,12)k\right)-0,05 &= f(0,17k)-0,05 \\ &= \left(0,17k + \dfrac{1}{4}\right)\text{e}^{-4 \times 0,17k} + \dfrac{5}{4} – 0,05 \\ &= \left(0,17k + \dfrac{1}{4}\right)\text{e}^{-4 \times 0,17k} + \dfrac{6}{5} \end{array}$$ Son aire est donc $\mathscr{A}_k = 0,12 \times \left(\left(0,17k + \dfrac{1}{4}\right)\text{e}^{-4 \times 0,17k} + \dfrac{6}{5}\right)$.
$\quad$ Les nombres $X$ et $S$ sont des nombres réels.
Initialisation :
$\quad$ On affecte à $S$ la valeur $0$
$\quad$ On affecte à $X$ la valeur $0$
Traitement :
$\quad$ Tant Que $X + 0,17 < 2$
$\qquad$ $S$ prend la valeur $S + 0,12 \times \left( \left(X + \dfrac{1}{4}\right) \text{e}^{-4X} + \dfrac{6}{5}\right)$
$\qquad$ $X$ prend la valeur $X + 0,17$
$\quad$ Fin de Tant Que
Affichage :
$\quad$ On affiche $S$
Spécialité 5 points
Une ville possède un réseau de vélos en libre service dont deux stations A et B se situent en haut d'une colline. On admet qu'aucun vélo des autres stations n'arrive en direction des stations A et B.
On constate pour chaque heure $n$ qu'en moyenne :
$\bullet $20$\,\%$ des vélos présents à l'heure $n - 1$ à la station A sont toujours à cette station.
60$\,\%$ des vélos présents à l'heure $n - 1$ à la station A sont à la station B et les autres sont dans d'autres stations du réseau ou en circulation.
$\bullet $10$\,\%$ des vélos présents à l'heure $n - 1$ à la station B sont à la station A, 30$\,\%$ sont toujours à la station B et les autres sont dans d'autres stations du réseau ou en circulation.
$\bullet $Au début de la journée, la station A comporte 50 vélos, la station B 60 vélos.
Partie A
Au bout de $n$ heures, on note $a_{n}$ le nombre moyen de vélos présents à la station A et $b_{n}$ le nombre moyen de vélos présents à la station B. On note $U_{n}$ la matrice colonne $\begin{pmatrix}a_{n}\\b_{n}\end{pmatrix}$ et donc $U_{0} = \begin{pmatrix}50\\60\end{pmatrix}$.
- Déterminer la matrice $M$ telle que $U _{n+1} = M \times U_{n}$.
- Déterminer $U_{1}$ et $U_{2}$.
- Au bout de combien d'heures reste-t-il un seul vélo dans la station A ?
Partie B
Le service décide d'étudier les effets d'un approvisionnement des stations A et B consistant à apporter après chaque heure de fonctionnement 30 vélos à la station A et 10 vélos à la station B. Afin de conduire cette étude, il décide de modéliser la situation présente de la manière suivante :
Au bout de $n$ heures, on note $\alpha_{n}$ le nombre moyen de vélos présents à la station A et $\beta_{n}$ le nombre moyen de vélos présents à la station B. On note $V_{n}$ la matrice colonne $\begin{pmatrix}\alpha_{n} \\\beta_{n}\end{pmatrix}$ et $V_{0} = \begin{pmatrix} 50\\60\end{pmatrix}$. Dans ces conditions $V_{n+1} = M \times V_{n} + R$ avec $R = \begin{pmatrix}30\\10\end{pmatrix}$ .
- On note $I$ la matrice $\begin{pmatrix}1&0\\0&1 \end{pmatrix}$ et $N$ la matrice $I - M$.
- On désigne par $V$ une matrice colonne à deux lignes. Montrer que $V = M \times V + R$ équivaut à $N \times V = R$ .
- On admet que $N$ est une matrice inversible et que $N^{- 1} = \begin{pmatrix}1,4&0,2\\1,2&1,6\end{pmatrix}$. En déduire que $V = \begin{pmatrix}44\\52\end{pmatrix}$
- Pour tout entier naturel $n$, on pose $W_{n} = V_{n} - V$.
- Montrer que $W_{n+1} = M \times W_{n}$.
- On admet que :
pour tout entier naturel $n, W_{n} = M^{n} \times W_{0}$,
pour tout entier naturel $n \geqslant 1,\:\: M^n = \dfrac{1}{2^{n-1}}\begin{pmatrix} 0,2&0,1\\ 0,6& 0,3\end{pmatrix}$.
Calculer, pour tout entier naturel $n \geqslant 1,\: V_{n}$ en fonction de $n$. - Le nombre moyen de vélos présents dans les stations A et B a-t-il tendance à se stabiliser ?
Correction de l'exercice de Spécialité 5 points
Une ville possède un réseau de vélos en libre service dont deux stations A et B se situent en haut d'une colline. On admet qu'aucun vélo des autres stations n'arrive en direction des stations A et B.
On constate pour chaque heure $n$ qu'en moyenne :
$\bullet $20$\,\%$ des vélos présents à l'heure $n - 1$ à la station A sont toujours à cette station.
60$\,\%$ des vélos présents à l'heure $n - 1$ à la station A sont à la station B et les autres sont dans d'autres stations du réseau ou en circulation.
$\bullet $10$\,\%$ des vélos présents à l'heure $n - 1$ à la station B sont à la station A, 30$\,\%$ sont toujours à la station B et les autres sont dans d'autres stations du réseau ou en circulation.
$\bullet $Au début de la journée, la station A comporte 50 vélos, la station B 60 vélos.
Partie A
Au bout de $n$ heures, on note $a_{n}$ le nombre moyen de vélos présents à la station A et $b_{n}$ le nombre moyen de vélos présents à la station B. On note $U_{n}$ la matrice colonne $\begin{pmatrix}a_{n}\\b_{n}\end{pmatrix}$ et donc $U_{0} = \begin{pmatrix}50\\60\end{pmatrix}$.
- Déterminer la matrice $M$ telle que $U _{n+1} = M \times U_{n}$. On a ainsi $a_{n+1} = 0,2a_n + 0,1b_n$ et $b_{n+1} = 0,6a_n + 0,3b_n$.
- Déterminer $U_{1}$ et $U_{2}$. $U_1 = M \times U_0 = \begin{pmatrix} 16 \\\\48 \end{pmatrix}$
- Au bout de combien d'heures reste-t-il un seul vélo dans la station A ? On a $U_3 = M \times U_1 = \begin{pmatrix} 4 \\\\ 12 \end{pmatrix}$
On a donc $M = \begin{pmatrix} 0,2 & 0,1 \\\\0,6 & 0,3 \end{pmatrix}$
$\quad$
$U_2 = M \times U_1 = \begin{pmatrix} 8 \\\\ 24 \end{pmatrix}$
$U_4 = M \times U_1 = \begin{pmatrix} 2 \\\\ 6 \end{pmatrix}$
$U_5 = M \times U_1 = \begin{pmatrix} 1 \\\\ 3 \end{pmatrix}$
Par conséquent au bout de $5$ heures, il ne reste plus qu’un seul véol dans la station A.
Partie B
Le service décide d'étudier les effets d'un approvisionnement des stations A et B consistant à apporter après chaque heure de fonctionnement 30 vélos à la station A et 10 vélos à la station B. Afin de conduire cette étude, il décide de modéliser la situation présente de la manière suivante :
Au bout de $n$ heures, on note $\alpha_{n}$ le nombre moyen de vélos présents à la station A et $\beta_{n}$ le nombre moyen de vélos présents à la station B. On note $V_{n}$ la matrice colonne $\begin{pmatrix}\alpha_{n} \\\beta_{n}\end{pmatrix}$ et $V_{0} = \begin{pmatrix} 50\\60\end{pmatrix}$. Dans ces conditions $V_{n+1} = M \times V_{n} + R$ avec $R = \begin{pmatrix}30\\10\end{pmatrix}$ .
- On note $I$ la matrice $\begin{pmatrix}1&0\\0&1 \end{pmatrix}$ et $N$ la matrice $I - M$.
- On désigne par $V$ une matrice colonne à deux lignes. Montrer que $V = M \times V + R$ équivaut à $N \times V = R$ . $V = M \times V + R \Leftrightarrow$ $V – M \times V = R \Leftrightarrow (I – M) \times V = R $ $\Leftrightarrow N \times V = R$
- On admet que $N$ est une matrice inversible et que $N^{- 1} = \begin{pmatrix}1,4&0,2\\1,2&1,6\end{pmatrix}$. En déduire que $V = \begin{pmatrix}44\\52\end{pmatrix}$ Puisque $N$ est inversible on a ainsi $V = N^{-1} \times R = \begin{pmatrix} 1,4 & 0,2\\\\1,2 & 1,6 \end{pmatrix} \times \begin{pmatrix} 30 \\\\ 10 \end{pmatrix} = \begin{pmatrix} 44 \\\\52 \end{pmatrix}$
- Pour tout entier naturel $n$, on pose $W_{n} = V_{n} - V$.
- Montrer que $W_{n+1} = M \times W_{n}$. $$\begin{array}{ll} W_{n+1} &= V_{n+1} – V = M \times V_n + R – V \\ &=M \times V_n + R – (M \times V + R) \\ &=M \times V_n – M \times V \\ &= M \times (V_n – V) \\ &= M \times W_n \end{array}$
- On admet que :
pour tout entier naturel $n, W_{n} = M^{n} \times W_{0}$,
pour tout entier naturel $n \geqslant 1,\:\: M^n = \dfrac{1}{2^{n-1}}\begin{pmatrix} 0,2&0,1\\ 0,6& 0,3\end{pmatrix}$.
Calculer, pour tout entier naturel $n \geqslant 1,\: V_{n}$ en fonction de $n$. $W_0= V_0 – V = \begin{pmatrix} 6 \\\\8 \end{pmatrix}$ - Le nombre moyen de vélos présents dans les stations A et B a-t-il tendance à se stabiliser ? On a donc $a_n = 2 \times \dfrac{1}{2^{n-1}} + 44$ et $b_n = 6 \times \dfrac{1}{2^{n-1}} + 52$.
$W_n = M_n \times W_0 = \dfrac{1}{2^{n-1}}\begin{pmatrix} 0,2 \times 6 + 0,1 \times 0,1 \\\\0,6 \times 6 + 0,3 \times 8 \end{pmatrix}$ $=\dfrac{1}{2^{n-1}} \begin{pmatrix} 2\\\\6\end{pmatrix}$
On a $V_n = W_n + V = \dfrac{1}{2^{n-1}}\begin{pmatrix}2\\\\6 \end{pmatrix} + \begin{pmatrix} 44 \\\\52 \end{pmatrix}$
or $\lim\limits_{n \to +\infty} \dfrac{1}{2^{n-1}} = 0$.
Donc $\lim\limits_{n \to +\infty} a_n = 44$ et $\lim\limits_{n \to +\infty} b_n = 52$.
Le nombre moyen de vélos présents dans les stations A et B se stabilise donc.
- Vues: 37469
