Baccalauréat S Métropole -La Réunion 9 septembre 2015 - Exercice 4
Page 7 sur 10
Exercice 4 : 3 points
On considère la fonction $f$ définie sur $]0~;~ +\infty[$ par \[f(x) = \dfrac{1}{x}(1 + \ln x)\]
- Dans les trois situations suivantes, on a dessiné, dans un repère orthonormé, la courbe représentative $\mathcal{C}_f$ de la fonction $f$ et une courbe $\mathcal{C}_F$. Dans une seule situation, la courbe $\mathcal{C}_F$ est la courbe représentative d'une primitive $F$ de la fonction $f$. Laquelle ? Justifier la réponse.
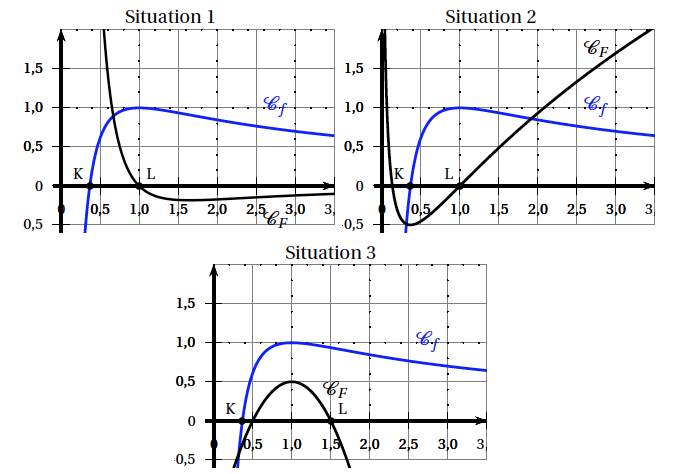
- Dans la situation retenue à la question 1, on appelle :
- K le point d'intersection de la courbe $\mathcal{C}_f$ et de l'axe des abscisses et $\mathcal{D}$ la droite passant par K et parallèle à l'axe des ordonnées ;
- L le point d'intersection de $\mathcal{C}_F$ et de l'axe des abscisses, ayant une abscisse supérieure à $\dfrac{1}{2}$ et $\Delta$ la droite passant par L et parallèle à l'axe des ordonnées.
- Déterminer une valeur approchée de l'aire du domaine du plan délimité par les droites $\mathcal{D}$ et $\Delta$, par la courbe $\mathcal{C}_f$ et par l'axe des abscisses.
- Peut-on déterminer la valeur exacte de cette aire ?
- Vues: 36034
