Baccalauréat S Métropole -La Réunion 9 septembre 2015 - Correction Exercice 2
Correction de l'exercice 2 (7 points)
Soit $f$ la fonction définie et dérivable sur l'intervalle $[0~;~ + \infty[$ telle que : $$f(x) = \dfrac{x}{\text{e}^x - x}$$ On admet que la fonction $f$ est positive sur l'intervalle $[0~;~ + \infty[$. On note $\mathcal{C}$ la courbe représentative de la fonction $f$ dans un repère orthogonal du plan. La courbe $\mathcal{C}$ est représentée en annexe, à rendre avec la copie .
Partie A
Soit la suite $\left(I_n\right)$ définie pour tout entier naturel $n$ par $I_n = \displaystyle\int_0^n f(x)\:\text{d}x$.
On ne cherchera pas à calculer la valeur exacte de $I_n$ en fonction de $n$.
- Montrer que la suite $\left(I_n\right)$ est croissante. Pour montrer que la suite $\left(I_n\right)$ est croissante, on va étudier le signe de $I_{n+1} – I_n$.
- On admet que pour tout réel $x$ de l'intervalle $[0~;~+ \infty[$,$\text{e}^x - x \geqslant \dfrac{\text{e}^x}{2}$.
- Montrer que, pour tout entier naturel $n,\:I_n \leqslant \displaystyle\int_0^n 2x \text{e}^{- x}\:\text{d}x$. Sur $[0;+\infty[$, $\text{e}^x-x \ge \dfrac{e^x}{2} \ge 0$ donc $\dfrac{1}{\text{e}^x-x} \le \dfrac{2}{\text{e}^x}$ et $\dfrac{x}{\text{e}^x-x} \le \dfrac{2x}{\text{e}^x}$ (cette dernière inégalité est due au fait que $x \ge 0$).
- Soit $H$ la fonction définie et dérivable sur l'intervalle $[0~;~+ \infty[$ telle que : \[H(x) = (- x - 1)\text{e}^{- x}\] Déterminer la fonction dérivée $H'$ de la fonction $H$. D’après l’énoncé $H$ est dérivable sur $[0;+\infty[$.
- En déduire que, pour tout entier naturel $n,\:I_n \leqslant 2$. Par conséquent une primitive de $x \mapsto 2x\text{e}^{-x}$ est $2H$.
$$\begin{align*} I_n &=\int_0^n \dfrac{x}{\text{e}^x-x}\mathrm{d}x \\\\
& \le \int_0^n \dfrac{2x}{\text{e}^x}\mathrm{d}x \\\\
& \le \int_0^n 2x\text{e}^{-x}\mathrm{d}x
\end{align*}$$
$\quad$
$\begin{align*} H'(x) &= -\text{e}^{-x} – (-x-1)\text{e}^{-x} \\\\
&=-\text{e}^{-x}+x\text{e}^{-x}+\text{e}^{-x} \\\\
&= x\text{e}^{-x}
\end{align*}$
$\quad$
Ainsi :
$$\begin{align*} \int_0^n 2x\text{e}^{-x}\mathrm{d}x &= \left[2H(x)\right]_0^n \\\\
&= 2(-n-1)\text{e}^{-n} -2(-1) \\\\
&= 2 – 2(n+1)\text{e}^{-n} \\\\
& \le 2
\end{align*}$$
Car $-2(n+1)\text{e}^{-x}<0$.
Par conséquent $I_n \le 2$.
$\quad$ - Montrer que la suite $\left(I_n\right)$ est convergente. On ne demande pas la valeur de sa limite. La suite $\left(I_n\right)$ est croissante et majorée par $2$; elle est donc convergente.
$$\begin{align*} I_{n+1} – I_n &= \int_0^{n+1} f(x) \mathrm{d}x- \int_0^n \mathrm{d}x \\\\
&= \int_n^{n+1} f(x)\mathrm{d}x
\end{align*}$$
Puisque la fonction $f$ est positive sur $[0;+\infty[$, on a alors $\displaystyle \int_n^{n+1} f(x)\mathrm{d}x > 0$.
La suite $\left(I_n\right)$ est bien croissante.
$\quad$
$\quad$
Partie B
On considère l'algorithme suivant dans lequel les variables sont
- $K$ et $i$ des entiers naturels, $K$ étant non nul;
- $A,\: x$ et $h$ des réels.
$$ \begin{array}{|l|X|}\hline \text{Entrée : } & \text{Saisir } K \text{entier naturel non nul}\\ \hline \text{Initialisation} & \text{Affecter à } A \text{ la valeur } 0\\ &\text{Affecter à } x \text{ la valeur } 0\\ &\text{Affecter à } h \text{ la valeur } \dfrac{1}{K}\\[7pt] \hline \text{Traitement } &\text{Pour } i \text{variant de 1 à } K\\ &\hspace{0,4cm}\begin{array}{|l} \text{ Affecter à } A \text{ la valeur } A + h \times f(x)\\ \text{ Affecter à } x \text{ la valeur } x + h\\ \end{array}\\ &\text{ Fin Pour} \\ \hline \text{ Sortie } &\text{Afficher } A\\ \hline \end{array} $$
- Reproduire et compléter le tableau suivant, en faisant fonctionner cet algorithme pour $K = 4$. Les valeurs successives de $A$ seront arrondies au millième. $$ \begin{array}{|c|c|c|}\hline i & A & x\\ \hline 1 & &\\ \hline 2 & &\\ \hline 3 & &\\ \hline 4 & &\\ \hline \end{array} $$ $$\begin{array}{|c|c|c|}
- En l'illustrant sur l'annexe à rendre avec la copie, donner une interprétation graphique du résultat affiché par cet algorithme pour $K = 8$.
- Que donne l'algorithme lorsque $K$ devient grand ?
\hline
i&A&x\\
\hline
1&0&0,25 \\
\hline
2&0,060&0,5\\
\hline
3&0,169&0,75\\
\hline
4&0,306&1\\
\hline
\end{array}$$
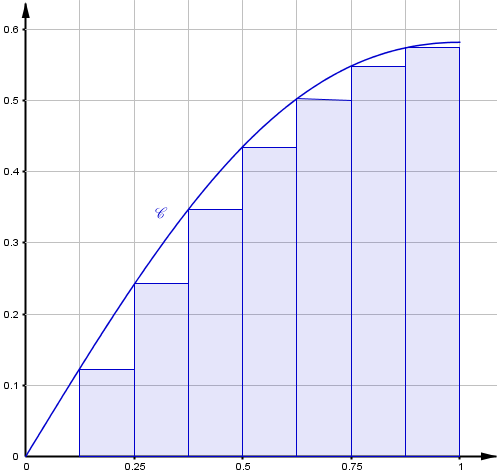
L’algorithme nous fournit l’aire des rectangles dessinés.
ANNEXE Exercice 2
À rendre avec la copie
Courbe $\mathcal{C}$, représentative de la fonction $f$ sur [0;6]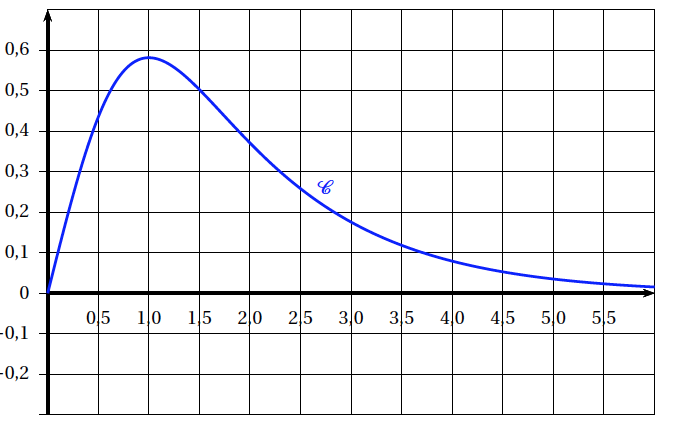
Courbe $\mathcal{C}$, représentative de la fonction $f$ sur [0;1]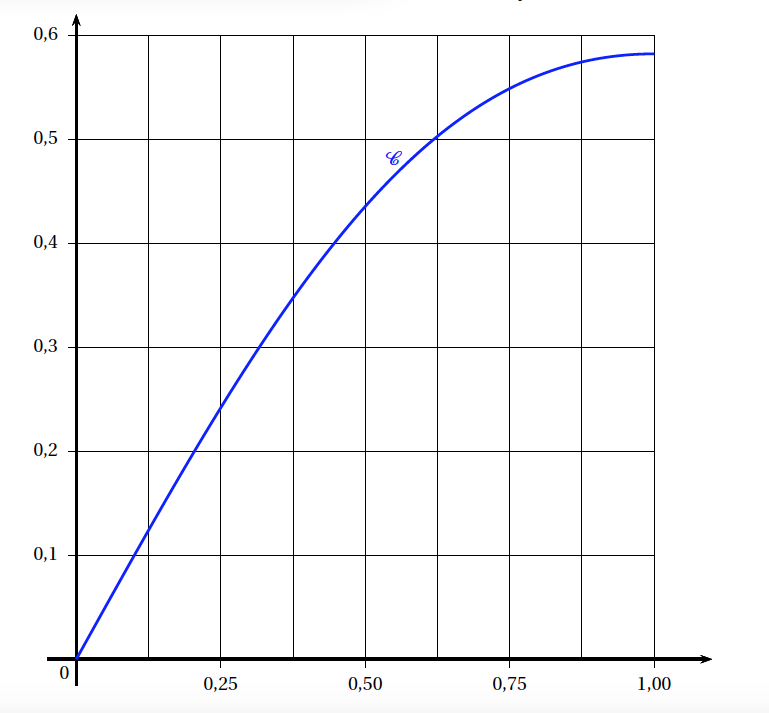
- Vues: 36027
