Baccalauréat S Liban 27 mai 2015 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (3 points)

Commun à tous les candidats

Fonctions

On considère la courbe $\mathcal{C}$ d'équation $y = \text{e}^x$, tracée ci-dessous.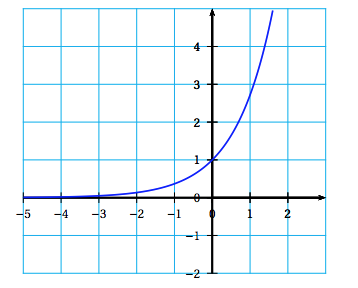

Pour tout réel $m$ strictement positif, on note $\mathcal{D}_m$ la droite d'équation $y = mx$.

1. Dans cette question, on choisit $m = \text{e}$. Démontrer que la droite $\mathcal{D}_{\text{e}}$, d'équation $y = \text{e}x$, est tangente à la courbe $\mathcal{C}$ en son point d'abscisse 1.
La fonction exponentielle est dérivable sur $\mathbb R$ de dérivée elle-même.
La tangente au point d’abscisse $1$ a pour équation $y=\text{e}^1(x-1) + \text{e}^1$ soit $y=\text{e} x$.
Ainsi $\mathscr{D}_{\text{e}}$ est bien tangente à la courbe $\mathscr{C}$ en son point d’abscisse $1$.

2. Conjecturer, selon les valeurs prises par le réel strictement positif $m$, le nombre de points d'intersection de la courbe $\mathcal{C}$ et de la droite $\mathcal{D}_m$.
On peut conjecturer que :
– si $0\le m<\text{e}$ il n’y a pas de point d’intersection
– si $m=\text{e}$ il y a un point d’intersection
– si $m>\text{e}$ il y a deux points d’intersection
$\quad$
3. Démontrer cette conjecture.
On appelle $f_m$ la fonction définie sur $\mathbb R$ par $f_m(x)= \text{e}^x-mx$
Cette fonction est dérivable sur $\mathbb R$ en tant que somme de fonctions dérivables.
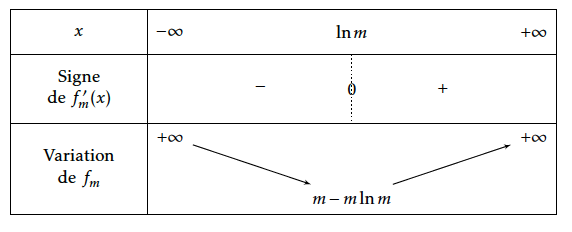
$f_m'(x)=\text{e}^x-m$.
$f_m'(x) > 0 \iff x > \ln m$.
On obtient ainsi le tableau de variations suivant :


En effet $\lim\limits_{x \to +\infty} f(x) = \lim\limits_{x \to +\infty} \text{e}^x \left(1 – mx\text{e}^{-x}\right) = +\infty$.
On utilise la limite usuelle : $ \lim\limits_{x \to +\infty} \dfrac{\text{e}^x}{x}= +\infty$ , d'où on déduit $ \lim\limits_{x \to +\infty} \dfrac{x}{\text{e}^x}= 0$
Et $\lim\limits_{x\to -\infty} \text{e}^x = 0$ donc $\lim\limits_{x \to -\infty} f_m(x) = +\infty$
Si $ 0 < m < \text{e} $ alors en appliquant la fonction $\ln$ strictement croissante sur $]0;+\infty[$, $\ln m< \ln\text{e}$, soit $\ln m< 1$
Alors $1-\ln m>0$ et $m>0$, donc le minimum $m(1-\ln m )$ de $f_m$ est strictement positif.
et la fonction $f_m$ est toujours positive sur $\mathbb R$.
$\mathscr{C}$ et $\mathscr{D}_m$ n’ont donc aucun point en commun.
$\quad$
Si $m=\text{e}$ il n’y a qu’un seul point commun car $m-m\ln m =\text{e}-\text{e}\ln \text{e}= 0$
$\quad$
Si $m> \text{e}$ Ainsi $m – m\ln m = m(1-\ln m) <0$.

D'après le théorème de la bijection :

• $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left]\2 ; \3\right]$.
• $\1$ est strictement décroissante sur l' intervalle $I = \left]\2 ; \3\right]$.
• $\lim\limits_{x \to \2}~\1(x)=\4$ et $\1 \left(\3\right)=\5$
$\1$ réalise donc une bijection de $\left]\2 ; \3\right]$ sur $\left[\5;\4\right[$
$\6\in \left[\5;\4\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left]\2 ; \3\right]$ .


D'après le théorème de la bijection :

• $\1 $ est une fonction dérivable  donc  continue  sur l' intervalle $I = \left[\2 ; \3\right[$.
• $\1$ est strictement croissante sur l' intervalle $I = \left[\2 ; \3\right[$.
• $\1 \left(\2\right)=\4$ et $\lim\limits_{x \to \3}~\1(x)=\5$
$\1$ réalise donc une bijection de $\left[\2 ; \3\right[$ sur $\left[\4;\5\right[$
$\6\in \left[\4;\5\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left[\2 ; \3\right[$ .

Il y a donc bien 2 points d’intersection.

Une animation Geogebra :