Bac STI2D Nouvelle-Calédonie 15 novembre 2016 - Exercice 2
Page 3 sur 8
Exercice 2 5 points
Pour chacune des cinq affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée.
Une réponse non justifiée n'est pas prise en compte.
- Considérons les deux nombres complexes $z_1 = \sqrt{2}\text{e}^{\text{i}\frac{3\pi}{4}}$ et $z_2 = 1 - \text{i}\sqrt{3}$ où i est le nombre complexe de module 1 et d'argument $\frac{\pi}{2}$.
Affirmation 1 : Le produit $z_1 \times z_2$ est égal à $2\sqrt{2}\text{e}^{\text{i}\frac{5\pi}{12}}$. - Affirmation 2 : La solution $f$ de l'équation différentielle $y" + 4y = 0$ qui vérifie $f(0) = - 1$ et $f'(0) = 2$ admet comme représentation graphique :
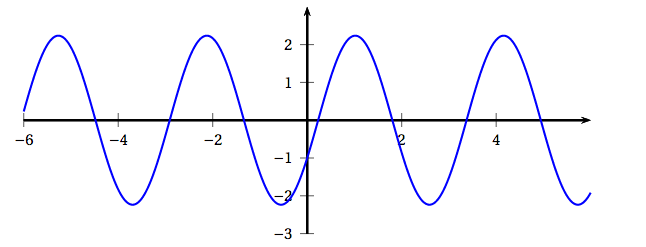
- Affirmation 3 : La solution de l'équation $\ln(x + 3) = 5$ est $\text{e}^5 - 3$.
- La durée de vie en heures d'un certain type d'ampoules électriques est modélisée par une variable aléatoire qui suit la loi exponentielle de paramètre $\lambda = 0,000125 \: \left(\text{exprimé en } \:h\right)$.
Affirmation 4 : En moyenne, la durée de vie d'une ampoule est 1250 h. - Affirmation 5 : la fonction $F(x) = x\ln x - x + 2$ est une primitive de la fonction $f(x) = \ln x$ sur l'intervalle $]0~;~+\infty[$.
Correction Exercice 2
- Vues: 18652
