Puissance 11 2015 Concours FEISIC
Calculatrice interdite ; traiter $12$ exercices sur les $16$ en $2$ h $30$ ; répondre par Vrai ou Faux sans justification. $+ 1$ si bonne réponse, $-1$ si mauvaise réponse, $0$ si pas de réponse, bonus d'un point pour un exercice entièrement juste.
Exercice 1
Étude de fonction
Soit $f$ une fonction dérivable sur $\mathbb R$ de courbe représentative $(\Gamma)$ dont la fonction dérivée $f'$ a pour représentation graphique la courbe ci-contre. On admet que $f'(x) = \left\{\begin{array}{l c l} 2x &\text{si} &x \leqslant 1\\ \dfrac{1}{x} + 1& \text{si}&x > 1 \end{array}\right.$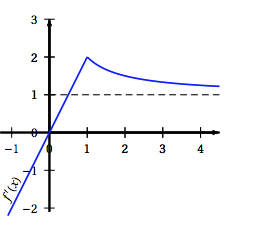
- La courbe $(\Gamma)$ admet une asymptote horizontale en $+ \infty$.
- Pour tout $x \in ]- \infty~;~1]$, $f(x) = x^2$. On suppose dans le c. et d. que $(\Gamma)$ passe par $\Omega(1~;~1)$.
- Pour tout $x \in \mathbb R$, $f(x) \geqslant 0$.
- $f( 2) = \ln 2 + 2$.
Exercice 2
Fonction définie par deux paramètres
Soit $a$ et $b$ deux réels strictement positifs fixés et $f$ la fonction définie sur $I = [- a~;~a]$ par $f(x) = \dfrac{b}{a}\sqrt{a^2 - x^2}$ de courbe représentative $(\Gamma)$.
- Pour tout $x \in I$, $f'(x) = \dfrac{b}{2 \times \sqrt{a^2 - x^2}}$.
- Si $a = 6$ et $b = 3$ alors pour tout $x \in I$, $f(x) \geqslant 3$.
- Si $a = b = 1$, alors l'équation $f(x) = \sqrt{2}$ admet deux solutions sur $I$.
- Si $a = b$ alors $(\Gamma)$ admet deux tangentes parallèles à la droite $(\Delta)$ d'équation $y = x - 5$.
Exercice 3
Bases de la géométrie
Les questions suivantes sont indépendantes.
- Le plan est muni d'un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ . Si la droite $(D)$ a pour équation paramétrique $\left\{\begin{array}{l c r} x&=&t\\ y&=&1 + t\\ z&=&2 + t \end{array}\right.$ avec $t$ réel, alors le vecteur $\vec{\imath} + \vec{\jmath} + \vec{k}$ est un vecteur directeur de $(D)$.
- Soit $a > 0$. Si ABC est un triangle équilatéral direct de côté $a$, alors $\vec{\text{AB}} \cdot \vec{\text{CA}} = \dfrac{a^2}{2}$. Pour le \text{c.} et \text{d.}, on suppose que le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$ .
- Le nombre $(1 + \text{i})^4$ est un nombre réel négatif.
- L'ensemble des points $M$ d'affixe $z$ telle que $|z + 4 - 3\text{i}| = 5$ est un cercle passant par l'origine du repère.
Exercice 4
Questions de logique
Agnan, Clotaire, Eudes, Geoffroy et Rufus ne s'entendent pas tous très bien. Pour la fête d'anniversaire qu'organisait le petit Nicolas, ils avaient prévenu :
- Clotaire refuserait de venir si Rufus était présent.
- Eudes ne viendrait que s'il était accompagné d'Agnan ou de Rufus.
- Quant à Geoffroy et Agnan, ils n'iraient nulle part l'un sans l'autre.
- Si Clotaire n'est pas venu à la fête, alors Rufus était présent.
- Si Rufus était absent, alors Clotaire est venu à la fête.
- Si Agnan est venu, alors Geoffroy et Eudes aussi.
- Si Eudes et Clotaire sont venus, alors Geoffroy était lui aussi présent.
Exercice 5
Petite démonstration
Soit $f$ la fonction définie sur $D_f = \mathbb R \backslash \left\{\frac{1}{2}\right\}$ par $f(x) = \dfrac{x^2}{2x - 1}$ de courbe représentative $(\Gamma)$ et $I = \left]\dfrac{1}{2}~;~+ \infty\right[$.
- Pour tout réel $x \in D_f,$ $f'(x) = \dfrac{2x(1 - x)}{(1 - 2x)^2}$.
- $(\Gamma)$ admet deux tangentes parallèles à la droite $(\Delta)$ d'équation $y = - x + 5$.
- Si $x \in I$, la fonction $k \::\: x \longmapsto \ln (f(x))$ admet comme dérivée la fonction $k': \:x \longmapsto \dfrac{2}{x} - \dfrac{2}{2x - 1}$.
- Pour tout $n \in \mathbb N$, on définit la suite $\left(u_n\right)$ par $\left\{\begin{array}{l c l} u_0&=&3\\ u_{n+1}&=&\dfrac{u_n^2}{2u_n - 1} \end{array}\right.$.
Afin d'étudier le sens de variation de la suite $\left(u_n\right)$ on effectue le raisonnement suivant :
« Pour tout $n \in \mathbb N$, on souhaite démontrer la relation « $u_{n+1} - u_n \geqslant 0$ ».
Si $x \in I$, alors $f'(x) > 0$ et la fonction $f$ est strictement croissante sur $I$.
Supposons que la relation soit vraie à un certain rang $k \in \mathbb N$, c'est-à-dire $u_{k+1} - u_k > 0$.
Par définition de la suite $\left(u_n\right)$ nous avons $u_{k+2} = f\left(u_{k+1}\right)$ et $u_{k+1} = f\left(u_k\right)$ avec $f$ strictement croissante sur $I$ ; donc si $u_{k+1} > u_k$ alors nous pouvons en déduire que $u_{k+2} = f\left(u_{k+1}\right) > u_{k+1} = f\left(u_k\right)$ soit $u_{k+2} > u_{k+1}$ ce qui nous permet de conclure que la relation est vraie au rang $k+ 1$.
Conclusion : la relation est héréditaire et, comme la fonction $f$ est strictement croissante sur $I$, nous pouvons en déduire que la suite $\left(u_n\right)_{n \geqslant 0}$ est strictement croissante ».
Ce raisonnement est correct.
Exercice 6
Calculs de limites
- $\displaystyle\lim_{x \to + \infty} \text{e}^{\frac{1}{x}} = 0$.
- $\displaystyle\lim_{x \to 0} \dfrac{1 - \text{e}^{- x}}{x} = 1$.
- Soit $f$ la fonction définie sur $]0~;~+ \infty[$ par $f(x) = \dfrac{\text{e}^{x} + 1}{\text{e}^{x} - x - 1}$. La courbe $(\Gamma)$ représentative de la fonction $f$ admet l'axe des abscisses comme asymptote horizontale.
- Pour tout $n \in \mathbb N$, la suite $\left(u_n\right)$ définie par $u_n = \dfrac{\sin (n) - 2n}{n+1}$ converge vers $0$.
Exercice 7
Calcul intégral
- $J = \displaystyle\int_1^{\text{e}} \dfrac{2x + 1}{x^2}\:\text{d}x = 3 + \dfrac{1}{\text{e}}$.
- $K = \displaystyle\int_1^{2} \dfrac{x}{\left(x^2 + 1\right)^2}\: \text{d}x = \dfrac{3}{20}$.
- Soit $\alpha$ un réel strictement positif, $\displaystyle\int_0^{\alpha} \dfrac{x}{1 + x}\:\text{d}x = \alpha - \ln (1 + \alpha)$.
- Soit $L = \displaystyle\int_{\text{e}}^{\text{e}^2} - x \ln (x)\:\text{d}x$. On a : $\text{e}^2\left(1 - \text{e}^2\right) \leqslant L \leqslant \dfrac{\text{e}^2}{2}\left(1 - \text{e}^2\right)$.
Exercice 8
Fonction exponentielle
Soit $F_1$ et $g$ les fonctions définies sur $\mathbb R$ respectivement par \[F_1(x) = \text{e}^{- x} - 2x \quad \text{et}\quad g(x) = \dfrac{\text{e}^{- x}( x + 1)}{\text{e}^{- x} + 2}.\] On désigne par $(C)$ la courbe représentative de la fonction $F_1$ et par $\left(x_n\right)$ la suite définie, pour tout $n \in \mathbb N$, par $x_0 = 1$ et $x_{n+1} = g\left(x_n\right)$.
- L'équation $F_1(x) = 0$ admet une unique solution $\alpha$ avec $0 < a < 1$. Dans les questions \text{b.}, \text{c.} et \text{d.}, on admet la convergence de la suite $\left(x_n\right)$.
- $\displaystyle\lim_{x \to + \infty} x_n = \alpha$.
- Si $a \in \mathbb R$, alors la tangente à $(C)$ en $x = a$ coupe l'axe des abscisses en un point d'abscisse $g(a)$. On donne le programme Prog ci-dessous :

- Pour $n = 5$, Prog affiche 0,3125 et $0,375$, nous pouvons en déduire que $ 0,3125 < \alpha < 0,375$.
Exercice 9
Fonction exponentielle et logarithme
Soit $f$ la fonction définie sur $]0~;~+\infty[$ par $f(x) = \dfrac{\ln \left(\text{e}^{2x} - 1 \right)}{\text{e}^x}$, $g$ la fonction définie sur $]1~;~+\infty[$ par $g(x) = 2x - (x - 1) \times \ln (x - 1)$ et $\varphi$ la fonction définie sur $]1~;~+\infty[$ par $\varphi(x) = \dfrac{\ln \left(x^2 - 1\right)}{x}$.
- $g'(x) = 1 + \ln \left(\dfrac{1}{x - 1}\right).$
- $\varphi'(x) = \dfrac{g\left(x^2\right)}{x^2}$.
- $g$ admet un minimum en $x = \text{e} + 1$. On admet qu'il existe une unique solution $\alpha$ à l'équation $g(x) = 0$ sur $]\text{e} + 1~;~+ \infty[$.
- $f\left(\ln \sqrt{\alpha}\right) = \dfrac{2\sqrt{\alpha}}{\alpha - 1}$.
Exercice 10
Suite et trigonométrie
Soit $\left(u_n\right)$ la suite définie, pour tout $n \in N$, par $u_n = (- 1)^n + 2 \times \sin \left(\dfrac{\pi}{4}n\right)$.
- Pour tout entier naturel $n$, on a : $u_{n + 8} > u_n$.
- Pour tout entier naturel $n$, on a : $- 3 \leqslant u_n \leqslant 3$.
- La suite $\left(u_n\right)$ est monotone.
- $\displaystyle\lim_{n \to + \infty} \dfrac{u_n}{n} = 0$.
Exercice 11
Suite de nombres complexes
On se place dans le plan complexe muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$ et on considère la suite $\left(z_n\right)$ de nombres complexes définie, pour tout $n \in \mathbb N$, par : $\left\{\begin{array}{l c l} z_0& =& 2\\ z_{n+1}&=&\dfrac{1 + \text{i}}{2}z_n \end{array}\right.$ On pose $A_n$ le point d'affixe $z_n$ et on définit, pour tout $n \in \mathbb N$, la suite $\left(u_n\right)$ par $u_n = \left|z_n\right|$.
- La suite $\left(u_n\right)$ est géométrique.
- Pour tout entier naturel $n$, $\dfrac{z_{n+1} - z_n}{z_{n+1}} = \text{i}$.
- À partir du rang $n = 4$, le point $A_n$ appartient au disque de centre O et de rayon $R = \dfrac{1}{2}$.
- Pour tout entier naturel $n$, le triangle O$A_nA_{n+1}$ est isocèle et rectangle.
Exercice 12
Géométrie et complexes
Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$ . On définit A et B deux points d'affixes respectives $z_{\text{A}} = 1$ et $z_{\text{B}} = 2\text{i}$ et $T$ la transformation complexe du plan qui, à tout point $M$ d'affixe $z$ non nulle, associe le point $M'$ d'affixe $z' = \dfrac{z - 2\text{i}}{z}$.
- L'image du point d'affixe $\text{e}^{\text{i}\frac{\pi}{4}}$ par la transformation $T$ est le point d'affixe $1 + 2\text{e}^{- \text{i}\frac{\pi}{4}}$.
- L'ensemble des points $M$ du plan complexe tels que O$M' = 1$ représente la médiatrice du segment [OB].
- $M'$ appartient au cercle de centre A et de rayon 1 si et seulement si le point $M$ appartient au cercle de centre O et de rayon $R = 2$.
- $z'$ est un nombre complexe imaginaire pur si et seulement si le point $M$ appartient au cercle de diamètre [OB].
Exercice 13
Variables aléatoires réelles : Cours - Calculs
$X$ est une variable aléatoire qui suit la loi exponentielle de paramètre $\lambda = 1$.
- Pour tout entier naturel $n$, on a : $P(X > n) = \dfrac{1}{\text{e}^n}$.
- Pour tout entier naturel $n$, on a : $P_{X>n}(X > n + 1) = P(X < 1)$. Soit $\sigma > 0$, $Y$ est une variable aléatoire qui suit la loi normale $\mathcal{N}\left(9~;~\sigma^2\right)$ et $Z$ la variable aléatoire définie par $Z = \dfrac{Y - 9}{\sigma}$
- $Z$ suit la loi normale $\mathcal{N}(0~;~1)$.
- $P(7 \leqslant Y \leqslant 11) = 2P\left(0 \leqslant Z \leqslant \dfrac{2}{\sigma}\right)$.
Exercice 14
Probabilités conditionnelles
Un acteur est sujet à des trous de mémoire. S'il relit son texte avant d'entrer en scène, la probabilité qu'il ait un trou de mémoire pendant la représentation vaut $\dfrac{1}{9}$, tandis que s'il ne relit pas son texte, cette probabilité vaut $\dfrac{1}{3}$. S'il a eu un trou de mémoire au cours d'une représentation, il relit forcément son texte avant la représentation suivante ; mais s'il n'a pas eu de trou de mémoire, il ne relit son texte qu'avec une probabilité de $\dfrac{1}{2}$. On suppose que l'acteur a relu son texte le soir de la première représentation.
- La probabilité qu'il ait eu un trou de mémoire lors de la première et de la deuxième représentation est de $\dfrac{1}{9}$.
- La probabilité qu'il ait eu un trou de mémoire à la deuxième représentation est de $\dfrac{25}{81}$.
- Sachant qu'il n'a pas eu de trou de mémoire le soir de la première, la probabilité qu'il n'en ait pas eu non plus à la deuxième représentation est de $\dfrac{7}{9}$. On note $p_n$ ($n$ étant un entier naturel non nul) la probabilité de l'évènement « l'acteur a eu un trou de mémoire lors de la $n$-ième représentation ».
- Pour tout entier $n \geqslant 1$, \: $p_{n+1} = \dfrac{2 - p_n}{9}$.
Exercice 15
Logique et géométrie dans l'espace
L'espace est muni d'un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ et $m$ et $p$ sont deux réels. On définit le plan $(P)$ ayant pour équation cartésienne $x - y + 2z - 3 = 0$ et $(\Delta)$ la droite passant par le point A de coordonnées $(2~;~p~;~1)$ et de vecteur directeur $\vec{u}\begin{pmatrix}- 1\\m\\1\end{pmatrix}$.
- Il existe au moins un réel $m$ tel que $(\Delta)$ soit parallèle à (P).
- Si $m = 1$, alors il existe au moins un réel $p$ tel que $(\Delta) \cap (P) = \emptyset$.
- Si $m \ne 1$, alors pour tout réel $p$, $(\Delta) \cap (P) \ne \emptyset$.
- Si $p = 1$, alors pour tout réel $m$,\: $(\Delta) \cap (P) = \{\text{A}\}$.
Exercice 16
Orthogonalité dans l'espace
SABCD est une pyramide régulière à base carrée ABCD. Le point O est le centre du carré ABCD, J est le milieu du segment [SO], F est le milieu du segment [BC] et K est le point défini par $\vec{\text{SK}} = \dfrac{1}{3} \vec{\text{SD}}$. 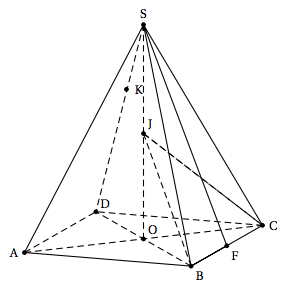
- $\vec{\text{BK}} = - \vec{\text{SB}} + \dfrac{1}{3}\vec{\text{SD}}$ et $\vec{\text{BJ}} = \dfrac{3}{4}\vec{\text{SB}} + \dfrac{1}{4}\vec{\text{SD}}$.
- B, K et J sont alignés.
- Les plans (BJC) et (SAD) sont sécants suivant une droite $(\Delta)$ orthogonale à la droite (SF). Pour le d., on suppose que BD = SO et on se place dans le repère orthonormé direct $\left(\text{O}~;~\vec{\text{OB}},~\vec{\text{OC}},~\vec{\text{OJ}}\right)$.
- La droite (KJ) coupe le plan (P) d'équation cartésienne $2x + 3y - z + 4 = 0$ au point $\Omega$ de coordonnées $(- 1~;~0~;~2)$.
- Vues: 9303
