Baccalauréat S Amérique du Sud 24 novembre 2015
Page 1 sur 10
Exercice 1 5 points
Partie A
Dans le plan muni d'un repère orthonormé $(,O;\vec{i},\vec{j} \,)$ on désigne par $\mathcal{C}_u$ la courbe représentative de la fonction $u$ définie sur l'intervalle $]0;+ \infty[$ par : \[u(x) = a + \dfrac{b}{x} + \dfrac{c}{x^2}\] où $a, b$ et $c$ sont des réels fixés. On a tracé sur le graphique ci-dessous la courbe $\mathcal{C}_u$ et la droite $\mathcal{D}$ d'équation $y = 1$.
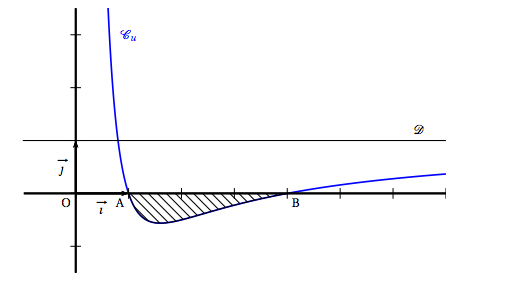
On précise que la courbe $\mathcal{C}_u$ passe par les points A(1;0) et B(4;0) et que l'axe des ordonnées et la droite $\mathcal{D}$ sont asymptotes à la courbe $\mathcal{C}_u$.
- Donner les valeurs de $u(1)$ et $u(4)$.
- Donner $\displaystyle\lim_{x \to + \infty} u(x)$. En déduire la valeur de $a$.
- En déduire que, pour tout réel $x$ strictement positif, $u(x) = \dfrac{x^2 - 5x + 4}{x^2}$.
Partie B
Soit $f$ la fonction définie sur l'intervalle $]0;+ \infty[$ par : \[f(x) = x - 5\ln x - \dfrac{4}{x}.\]
- Déterminer la limite de $f(x)$ lorsque $x$ tend vers $0$. On pourra utiliser sans démonstration le fait que $\displaystyle\lim_{x \to 0} x \ln x = 0$.
- Déterminer la limite de $f(x)$ lorsque $x$ tend vers $+ \infty$.
- Démontrer que, pour tout réel $x$ strictement positif, $f'(x) = u(x)$. En déduire le tableau de variation de la fonction $f$ en précisant les limites et les valeurs particulières.
Partie C
- Déterminer l'aire $\mathcal{A}$, exprimée en unité d'aire, du domaine hachuré sur le graphique de la \textbf{partie A}.
- Pour tout réel $\lambda$ supérieur ou égal à 4, on note $\mathcal{A}_{\lambda}$ l'aire, exprimée en unité d'aire, du domaine formé par les points $M$ de coordonnées $(x;y)$ telles que \[4 \leqslant x \leqslant \lambda\quad \text{et}\quad 0 \leqslant y \leqslant u(x).\] Existe-t-il une valeur de $\lambda$ pour laquelle $\mathcal{A}_{\lambda} = \mathcal{A}$ ? Dans cette question, toute trace de recherche, même incomplète, ou d'initiative, même non fructueuse, sera prise en compte dans l'évaluation.
- Vues: 48072
