Baccalauréat S Métropole 20 juin 2013 - Correction Exercice 1
Page 2 sur 10
Correction de l'exercice 1 (4 points)
-
- Un arbre pondéré représentant la situation :
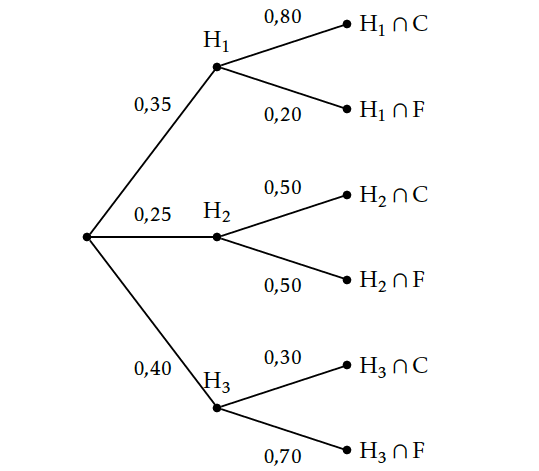
- On veut calculer $p\left (H_3\cap C\right )=p\left (H_3 \right )\times p_{H_3}\left (C\right )=0,40\times 0,50=0,20$
$p\left (H_3\cap C\right )=0,20$ - Calculons la probabilité de l'événement $C$.
$C=\left (H_1\cap C \right )\cup \left (H_2\cap C \right )\left (H_3\cap C \right )$.
La formule des probabilités totales donne
$$p\left (H_1\cap C \right )+p \left (H_2\cap C \right )+p\left (H_3\cap C \right )=p(H_1)\times p_{H_1}(C)+p(H_2) \times p_{H_2}(C)+p(H_3)\times p_{H_3}(C)$$
soit $p(C)= 0,35\times 0,80+ 0,25\times 0,50+ 0,40\times 0,30=0,525$
$p(C)=0,525$ - On veut calculer la probabilité de l'événement &\laquo; L'arbre a été acheté chez $H_1$ sachant que c'est un conifère&\raquo; .
soit à calculer la probabilité conditionnelle $p_{C}\left (H_1\right )=\dfrac{p\left (H_1\cap C\right )}{p(C)}=\dfrac{0,35\times 0,80}{0,525}$
$p_{C}\left (H_1\right )\approx 0,533$
- Un arbre pondéré représentant la situation :
-
- On est en présence d'un schéma de Bernoulli: Succès : &\laquo; l'arbre choisi au hasard est un conifère &\raquo; avec la probabilité $p=0,525 $
Echec : &\laquo; l'arbre choisi au hasard est un arbre à feuilles&\raquo; avec la probabilité $q=1-p= 0,475$
On répète 10 fois cette expérience de façon indépendante et on considère la variable aléatoire $X$ qui comptabilise le nombre de succès .
$X$ suit la loi binomiale $\mathcal{B}\left (10;0,525\right )$ de paramètres $n=10$ et $p=0,525$ - Calculons la probabilité que l'échantillon prélevé contienne exactement 5 conifères et donnons-en une valeur approchée à $10^{-3}$, près.
Pour tout entier $k \in[0;10]$; on a : $$p(X=k)=\binom{10}{k}\times 0,525^k\times0,475^{10-k}.$$ On veut $p(X=5) \binom{10}{5}\times 0,525^5\times0,475^5.$
$p(X=5)\approx 0,243$ - Calculons la probabilité que l'échantillon prélevé contienne au moins deux arbres feuillus et donnons-en une valeur approchée à $10^{-3}$, près.
On veut calculer ici la probabilité de l'événement $X\leq 8$
$p(X \leq 8)=1-p(X>8)=1-p(X=9)-p(X=10)=1-\binom{10}{9}\times 0,525^9\times0,475^1-\binom{10}{10}\times 0,525^10 \approx 0,984 $
La probabilité que l'échantillon prélevé contienne au moins deux arbres feuillus est environ $0,984$ à $10^{-3}$, près.
Remarque :$P(X\leq 8)$ peut s'obtenir avec la calculatrice par :$binomFR\text{é}p(10,0.525,8)$
- On est en présence d'un schéma de Bernoulli: Succès : &\laquo; l'arbre choisi au hasard est un conifère &\raquo; avec la probabilité $p=0,525 $
- Vues: 45551
