Baccalauréat S Amérique du Sud 21 novembre 2013 - Correction de l'Exercice 4
Page 8 sur 11
Exercice 4 5 points
Le plan complexe est rapporté à un repère orthonormé direct. On considère l'équation
\[(E) :\quad z^2 - 2z\sqrt{3} + 4 = 0.\]
- Résoudre l'équation $(E)$ dans l'ensemble $\mathbb{C}$ des nombres complexes. $z^2-2z\sqrt{3}+4 = 0$.
- Son discriminant est $\Delta = 4 \times 3 – 16 = -4 < 0$.
- Par conséquent $(E)$ possède $2$ racines complexes :
- On considère la suite $\left(M_{n}\right)$ des points d'affixes $z_{n} = 2^n \text{e}^{\text{i}(- 1)^n\frac{\pi}{6}}$, définie pour $n \geqslant 1$.
- Vérifier que $z_{1}$ est une solution de $(E)$. $z_1 = 2\text{e}^{-\text{i}\pi /6} = 2 \left( \dfrac{\sqrt{3}}{2} – \dfrac{\text{i}}{2} \right) = \sqrt{3} – \text{i}$. Donc $z_1$ est une solution de $(E)$.
- Écrire $z_{2}$ et $z_{3}$ sous forme algébrique. $z_2 = 4\text{e}^{\text{i}\pi /6} = 4 \left(\dfrac{\sqrt{3}}{2} + \dfrac{\text{i}}{2} \right) = 2\sqrt{3} + 2\text{i}$ et $z_3 = 8\text{e}^{-\text{i}\pi/6} = 8 \left(\dfrac{\sqrt{3}}{2} – \dfrac{\text{i}}{2} \right) = 4\sqrt{3} – 4\text{i}$
- Placer les points $M_{1},\: M_{2},\: M_{3}$ et $M_{4}$ sur la figure donnée en annexe et tracer, sur la figure donnée en annexe, les segments $\left[M_{1}, M_{2}\right],\: \left[M_{2}, M_{3}\right]$ et $\left[M_{3}, M_{4}\right]$.
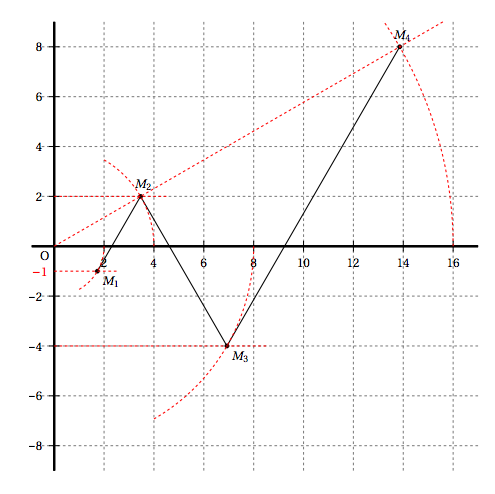
- Montrer que, pour tout entier $n \geqslant 1$, $z_{n} = 2^n \left(\dfrac{\sqrt{3}}{2} + \dfrac{(- 1)^n \text{i}}{2}\right)$. $z_n = 2^n \left( \cos \left( (-1)^n \dfrac{\pi}{6} \right) + \text{i} \sin \left((-1)^n\dfrac{\pi}{6} \right) \right) $
- $$ \dfrac{2\sqrt{3} – 2\text{i}}{2} = \sqrt{3} – \text{i} \quad \text{et} \quad \sqrt{3} + \text{i}$$.
- Calculer les longueurs $M_{1}M_{2}$ et $M_{2}M_{3}$. $M_1M_2 = |z_2 – z_1| = |\sqrt{3} + 3\text{i}| = \sqrt{12} = 2\sqrt{3}$
- $z_n=2^n \left( \cos \left( \dfrac{\pi}{6} \right) + (-1)^n \text{i} \sin \left(\dfrac{\pi}{6} \right) \right) = 2^n \left(\dfrac{\sqrt{3}}{2} + \dfrac{(-1)^n\text{i}}{2} \right)$
- $M_2M_3 = |z_3 – z_2| = |2\sqrt{3} -6\text{i}| = \sqrt{48} = 4\sqrt{3}$
- Pour la suite de l'exercice, on admet que, pour tout entier $n \geqslant 1$, $M_{n}M_{n+1} = 2^n \sqrt{3}$.
- On note $\ell_n = M_{1}M_{2} + M_{2}M_{3} + \cdots + M_{n}M_{n+1}$.
- Montrer que, pour tout entier $n \geqslant 1,\; \ell_n = 2\sqrt{3}\left(2^n - 1\right)$. On a donc :
- $l_n = \sqrt{3}(2 + 2^2 + \ldots + 2^n) = \sqrt{3}(1 + 2 + 2^2 + \ldots + 2^n – 1) = \sqrt{3} \left(\dfrac{1 – 2^{n+1}}{1 – 2} – 1 \right)$.
- $l_n = \sqrt{3}(2^{n+1} – 2) = 2\sqrt{3}(2^n – 1)$.
- Déterminer le plus petit entier $n$ tel que $\ell_n \geqslant 1000 $. On veut que $l_n \ge 1000 \Leftrightarrow 2^n – 1 \ge \dfrac{1000}{2\sqrt{3}} \Leftrightarrow 2^n \ge \dfrac{\sqrt{3} + 500}{\sqrt{3}} \Leftrightarrow n \text{ln }2 \ge \text{ln } \dfrac{\sqrt{3} + 500}{\sqrt{3}}$
- donc $n \ge \dfrac{\text{ln } \dfrac{\sqrt{3} +500}{\sqrt{3}}}{\text{ln }2}$.
- Par conséquent le plus petit entier $n$ tel que $l_n \ge 1000$ est $9$.
- Vues: 55154
