Baccalauréat S Amérique du Sud 21 novembre 2013 - Correction Exercice 1
Page 2 sur 11
Partie A
Soit $f$ la fonction définie sur $\mathbb{R}$ par
\[f(x) = x \text{e}^{1-x}.\]
- Vérifier que pour tout réel $x,\: f(x)= \text{e} \times \dfrac{x}{\text{e}^x}$. $f(x)=x\text{e}^{1-x} = x\text{e} \times \text{e}^{-x} = x\text{e} \times \dfrac{1}{\text{e}^x} = \text{e} \times \dfrac{x}{\text{e}}$
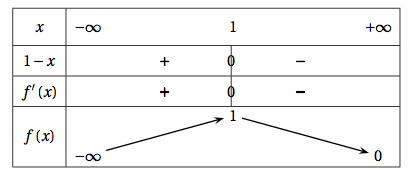
- Déterminer la limite de la fonction $f$ en $- \infty$. $\lim\limits_{x \rightarrow -\infty} \dfrac{1}{\text{e}^x} = +\infty$ donc $\lim\limits_{x \rightarrow -\infty} \dfrac{x}{\text{e}^x} = -\infty$ et $\lim\limits_{x \rightarrow -\infty} f(x)=-\infty$
- Déterminer la limite de la fonction $f$ en $+ \infty$. Interpréter graphiquement cette limite. $\lim\limits_{x \rightarrow +\infty} \dfrac{\text{e}^x}{x}=+\infty$ donc $\lim\limits_{x \rightarrow +\infty} \dfrac{x}{\text{e}^x} = 0^+$ et $\lim\limits_{x \rightarrow +\infty} f(x) = 0^+$
- Déterminer la dérivée de la fonction $f$. $f$ est un produit de fonctions dérivables sur $\mathbb R$, par conséquent $f$ est dérivable sur $\mathbb R$.
- Comme $\lim\limits_{x \rightarrow +\infty} f(x) = 0^+$, on déduit que la droite d'équation $y=0$ est asymptote horizontale à $\mathcal{C}_f$ au voisinage de $+\infty$.
- $f'(x) = \text{e}^{1-x} – x\text{e}^{1-x} = (1-x)\text{e}^{1-x}$
- Étudier les variations de la fonction $f$ sur $\mathbb{R}$ puis dresser le tableau de variation. La fonction exponentielle étant toujours positive, le signe de $f'(x)$ ne dépend donc que du signe de $1-x$.
Partie B
Pour tout entier naturel $n$ non nul, on considère les fonctions $g_{n}$ et $h_{n}$ définies sur $\mathbb{R}$ par :
\[g_{n}(x) = 1 + x + x^2 + \cdots + x^n \quad \text{et}\quad h_{n}(x) = 1 + 2x + \cdots + nx^{n-1}.\]
- Vérifier que, pour tout réel $x :\: (1 - x)g_{n}(x) = 1 - x^{n+1}$.
On obtient alors, pour tout réel $x \neq 1 :\:\: g_{n}(x) = \dfrac{1 - x^{n+1}}{1 - x}$.
$(1-x)g_n(x) = 1 +x + x^2 + \ldots+x^n – (x + x^2 + x^3+ \ldots + x^n+x^{n+1}) = 1-x^{n+1}$ (ce sont des sommes télescopiques).
- Comparer les fonctions $h_{n}$ et $g'_{n}$, $g'_{n}$ étant la dérivée de la fonction $g_{n}$. En déduire que, pour tout réel $x \neq 1 :\: h_{n}(x) = \dfrac{nx^{n+1} -(n+1)x^n + 1}{(1-x)^2}$. $ g’_n(x) = 0 + 1 + 2x + 3x^2 + \ldots + nx^{n-1} = h_n(x)$
- Or $g’_n(x) = \dfrac{-(n+1)x^n(1-x)+(1-x^{n+1})}{(1-x)^2}$.
- Soit $S_{n} = f(1) + f(2) + ... + f(n)$, $f$ étant la fonction définie dans la partie A. En utilisant les résultats de la partie B , déterminer une expression de $S_{n}$ puis sa limite quand $n$ tend vers $+ \infty$. $S_n = 1 + 2\text{e}^{-1} + 3\text{e}^{-2}+ \ldots + n\text{e}^{1-n}$
- Donc $h_n(x) = \dfrac{nx^{n+1}-(n+1)x^n+1}{(1-x)^2}$
- $S_n = h_n(\text{e}^{-1}) = \dfrac{n\text{e}^{-n-1}-(n+1)\text{e}^{-n}+1}{(1-\text{e}^{-1})^2}$
- $S_n= \dfrac{\dfrac{n}{\text{e}^{n+1}} – \dfrac{n+1}{\text{e}^{n}}+1}{(1-\text{e}^{-1})^2}$
- $\lim\limits_{n \rightarrow +\infty} \dfrac{n}{\text{e}^n} = 0$ et $\lim\limits_{n \rightarrow +\infty} \dfrac{n+1}{\text{e}^n} = 0$ par conséquent $\lim\limits_{n \rightarrow +\infty} S_n = \dfrac{1}{(1-\text{e}^{-1})^2}$
- Vues: 55152
