Bac STI2D Polynésie 9 juin 2016 - Correction Exercice 4
Page 8 sur 8
Exercice 4 6 points
Partie A : Lecture graphique
On considère la courbe $C$ associée à une fonction $f$ représentée en ANNEXE 2 avec la droite T, tangente à la courbe $C$ au point d'abscisse $0$.
- Résoudre graphiquement sur l'intervalle $[- 1~;~1,5]$ et avec la précision permise par le dessin les deux inéquations suivantes:
- $f(x) \geqslant 1$ Les solutions de l'inéquation $f(x)\geq 1$ sont les abscisses des points situés au dessus de la droite d'équation $y=1$. On lit àla précision du dessin : $$\mathcal{S}= [-1; -0,8] \cup [0; +\infty[$$
- $f'(x) \geqslant 0$. D'après le graphique $f$ est croissante sur $[x(S); +1,5]$.
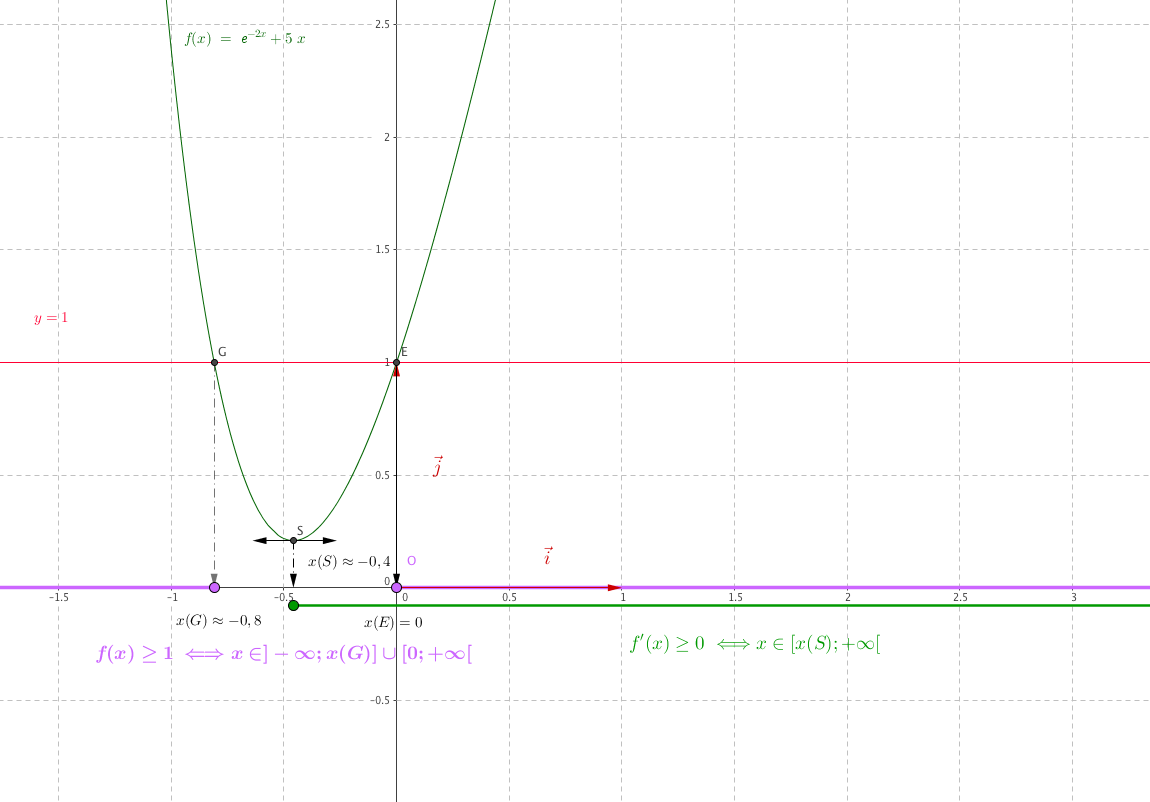
L'ensemble des solutions de l'inéquation $f'(x)\geq 0$ est : $$\mathcal{S}= [-0,4; 1,5]$$ -
- Donner l'équation. de la tangente T à la courbe $C$ au point de coordonnées (0 ; 1) en sachant que cette tangente passe par le point de coordonnées P(2 ; 7). $T$ a une équation du type $y=mx+p$ où \begin{align*} m&=\dfrac{y_P-y_E}{x_P-x_E} \\ &= =\dfrac{4-1}{1-0} \\ &=3\\ \end{align*} Donc $T: y=3x+p$ Comme $E(1,0)\in T$ on déduit $y_E=3x_E+p$ ce qui donne $1=3\times 0 + 1$ soit $p=1$
- En déduire le nombre dérivé $f'(0)$. $f'(0)$ est le coefficient directeur de la tangente $T$ au point d'abscisse 0
d'après la question précédente $f'(0)= 3$.
Partie B : Étude de la fonction $f$
Soit $f$ la fonction définie sur $\mathbb R$ par la relation $f(x) = \text{e}^{-2x} + 5x$.
- Déterminer, en la justifiant, la limite de $f$ en $+ \infty$. On admet pour la suite que la limite de $f$ en $- \infty$ est $+ \infty$. $\left.\begin{array}{l} \lim\limits_{-2x \to +\infty} =-\infty\\ \lim\limits_{t \to -\infty}~\text{e}^t=0 \end{array}\right\}$ par composée on obtient: $\lim\limits_{x \to +\infty}\text{e}^{-2x} =0$
- Calculer $f'(x)$ et étudier son signe sur $\mathbb R$. Comme $\left(\text{e}^u\right)'=u'\text{e}^u$, on obtient $$f'(x)=-2\text{e}^{-2x}+5$$ Etudions le signe de la dérivée :
- \begin{align*} f'(x)=0 &\iff -2\text{e}^{-2x}+5=0 \\ &\iff - 2\text{e}^{-2x} =-5 \\ &\iff \text{e}^{-2x} = \dfrac{5}{2}\\ &\iff -2x =\ln\left (\dfrac{5}{2}\right )\\ &\iff x=-\dfrac{1}{2}\ln\left (\dfrac{5}{2}\right )\\ \end{align*}
- \begin{align*} f'(x)>0 &\iff -2\text{e}^{-2x}+5>0 &\\ &\iff - 2\text{e}^{-2x} >-5 &\\ &\iff \text{e}^{-2x} < \dfrac{5}{2}& \text{en divisant par } -2< 0\\ &\iff -2x < \ln\left (\dfrac{5}{2}\right )&\text{en appliquant } \ln \text{strictement croissante sur }]0; +\infty[\\ &\iff x>-\dfrac{1}{2}\ln\left (\dfrac{5}{2}\right )&\text{en divisant par } -2< 0 \\ \end{align*}
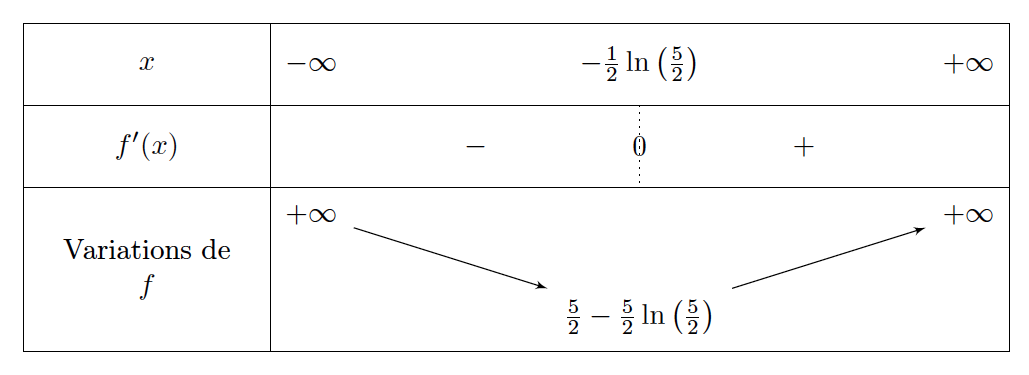
- En déduire le tableau des variations de la fonction $f$ sur $\mathbb R$. On déduit le tableau de variations de $f$ sur $\mathbb R$:
-
- Déterminer à partir du tableau des variations le nombre de solutions de l'équation $f(x) = 2$. D'après le tableau de variation de $f$ l'équation $f(x)=2$ a deux solutions :
- une notée $x_1$ dans $]-\infty; \alpha]$
- une autre notée $x_2$ dans $[ \alpha; +\infty[$
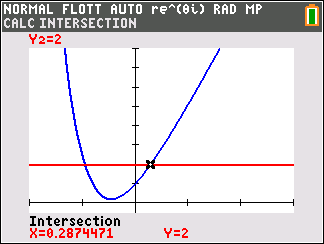
- Donner une valeur arrondie à $10^{-2}$ près de chaque solution. Avec les outils graphiques de la calculatrice on obtient :
- $x_1\approx 0,96 $
- $x_2\approx 0,29$
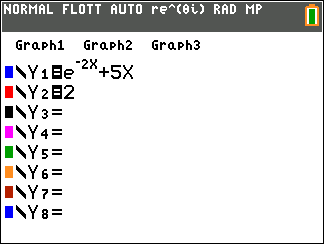
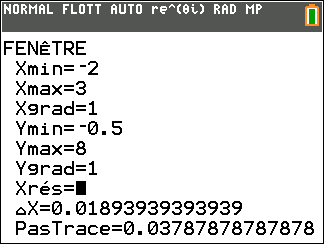
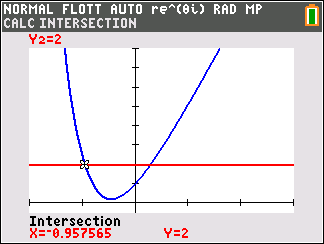
$\left.\begin{array}{l} \lim\limits_{x \to +\infty} \text{e}^{-2x} =0\\ \lim\limits_{ x \to +\infty}~5x=+\infty \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to +\infty} f(x)=+\infty$
$f\left(-\dfrac{1}{2}\ln\left (\dfrac{5}{2}\right )\right ) =f(\alpha)=\text{e}^{-2\alpha} + 5\alpha $
Comme $f'(\alpha)=0$ on déduit $-2\text{e}^{-2\alpha} + 5=0$ donc $ \text{e}^{-2\alpha}=\dfrac{5}{2}$
Ainsi $f(\alpha)=\dfrac{5}{2} - \dfrac{5}{2}\ln\left (\dfrac{5}{2}\right ) $
Partie C. : Calcul d'aire
On admet :
- que la courbe $C$ de la partie A est la représentation de la fonction $f$ définie dans la partie B ;
- que la courbe $C$ se situe « au-dessus » de la droite tangente T sur $\mathbb R$.
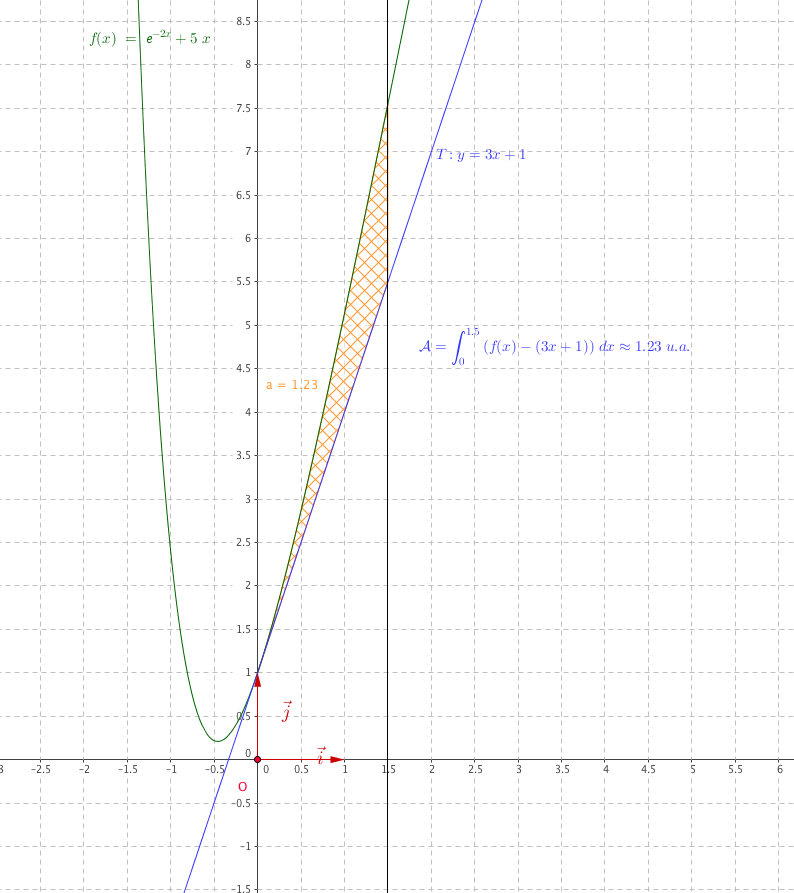
L'objectif de cette partie est de déterminer par un calcul l'aire $\mathcal{A}$ comprise entre la courbe $C$, la droite T et les droites verticales d'équations $x = 0$ et $x = 1,5$.
- Hachurer sur le dessin, en ANNEXE 2, l'aire $\mathcal{A}$ que l'on veut déterminer.
-
- Déterminer une primitive de la fonction $g$ définie sur $\mathbb R$ par : \[\text{pour tout réel }\:x,\: g(x) = \text{e}^{-2x} + 2x - 1.\] On utilise deux résultats du cours :
- La primitive d'une somme est la somme des primitives.
- $x\mapsto \text{e}^{ax}$ admat pour primitive $x\mapsto \dfrac{1}{a}\text{e}^{ax}$
- Justifier que l'aire $\mathcal{A}$ recherchée vaut, en unité d'aire: \[\mathcal{A} = \displaystyle\int_0^{1,5} g(x)\:\text{d}x.\] Déterminons tout d'aboerd une équation de T:
- En déduire la valeur exacte puis l'arrondi à $10^{- 2}$ de $\mathcal{A}$.
$\begin{align*} \mathcal{A} &= \displaystyle\int_0^{1,5} g(x)\:\text{d}x.\\ &=G(1,5)-G(0)\\ G(1,5)=-\dfrac{1}{2} \text{e}^{-2\times 1,5} + 1,5^2 - 1,5=-\dfrac{1}{2} \text{e}^{-3}+0,75 &\quad G(0)=-\dfrac{1}{2} \text{e}^{-2\times 0} + 0^2 - 0=-0,5\\ \mathcal{A} &= -\dfrac{1}{2} \text{e}^{-3}+0,75+0,5\\ \mathcal{A} &= -\dfrac{1}{2} \text{e}^{-3}+\dfrac{5}{4}\\ &\approx 1,23\end{align*}$
$T: y=f'(0)(x-0)+f(0)$, ici $f(0)=1$ et $f'(0)=3$
On déduit donc : $$T:y=3x+1$$ D'après l'énoncé la courbe $C$ se situe « au-dessus » de la droite tangente T sur $\mathbb R$,
L'aire $\mathcal{A}$ est donc
$$\begin{align*} \mathcal{A} &= \displaystyle\int_0^{1,5} \left(f(x)-y_T\right)\:\text{d}x\\ &= \displaystyle\int_0^{1,5} \left(f(x)-3x-1\right)\:\text{d}x\\ &= \displaystyle\int_0^{1,5} \left(\text{e}^{-2x} + 5x-3x-1\right)\:\text{d}x\\ &= \displaystyle\int_0^{1,5} \left(\text{e}^{-2x} + 2x -1\right)\:\text{d}x\\ &= \displaystyle\int_0^{1,5} g(x)\:\text{d}x. \end{align*}$$
- Vues: 20778
