Bac STI2D Polynésie 9 juin 2016 - Correction Exercice 3
Correction de l'exercice 3 (5 points)
Deux amis ont monté un atelier associatif pour réparer des vélos. Le but de cette association est que chaque adhérent puisse venir réparer son vélo dans cet atelier avec l'aide d'un spécialiste. Le matériel et les outils sont fournis. Les trois parties de cet exercice peuvent être traitées de manière indépendante
Partie A : les roulements à billes
Nos deux amis commandent régulièrement des lots de $60$ roulements à billes pour les vélos. Ils ont constaté que, lors de leur dernière livraison, sur le lot des $60$ roulements à billes, $3$ étaient défectueux. Ils s'inquiètent donc de la fiabilité du fabricant. Le contrat précise que seulement 4% des pièces sont défectueuses.
- Calculer la fréquence des pièces défectueuses dans le dernier lot. On considère que les pièces constituant ce lot forment un échantillon prélevé de façon aléatoire dans un stock dans lequel 4% des pièces sont défectueuses. La fréquence des pièces défectueuses est $f= \dfrac{3}{60}= \dfrac{1}{20}=0,05$
- Déterminer l'intervalle de fluctuation asymptotique à 95% de la fréquence des roulements à billes non conformes dans un échantillon de $60$ roulements. Les valeurs approchées seront arrondies à $10^{-2}$.
On rappelle que l'intervalle de fluctuation asymptotique à 95% sur un échantillon de taille $n$, avec $p$ la proportion de pièces défectueuses sur la population, est : \[\left[p - 1,96\sqrt{\dfrac{p(1 - p)}{p}}~;~p + 1,96\sqrt{\dfrac{p(1 - p)}{p}}\right]\] - Nos amis ont-ils raison de s'inquiéter ? Justifier votre réponse. Comme $f\in I_{60}$ . Nos amis n'ont pas raison de s'inquiéter. L'écart constaté entre le 5% observé dans l'échantillon et e 4% attendu est dû à des fluctuations d'échantillonnage.
- Méthode 1 :
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$ - Méthode 2 :
On remarque que $P(5,9 \leqslant D \leqslant 6,1)= P(\mu-2\sigma \leqslant D \leqslant \mu+2\sigma)\approx 0,954$ d'après un résultat du cours. - Démontrer que $\lambda = 0,0016 $.
- Méthode 1 :
On sait que $E(X)= \dfrac{1}{\lambda}$ donc $\lambda = \dfrac{1}{E(X)} =\dfrac{1}{625}=0,0016$ - Méthode 2 :
La densité d'une loi exponentielle de paramètre $\lambda$ est définie sur $[0; +\infty[$ par $f(x)= \lambda\text{e}^{- \lambda x}$
On a donc $f(0)=\lambda \text{e}^{0}= \lambda$
Par ailleurs on lit graphiquement $f(0)= 0,0016$ , on déduit donc $$\lambda = 0,0016 $$
- Méthode 1 :
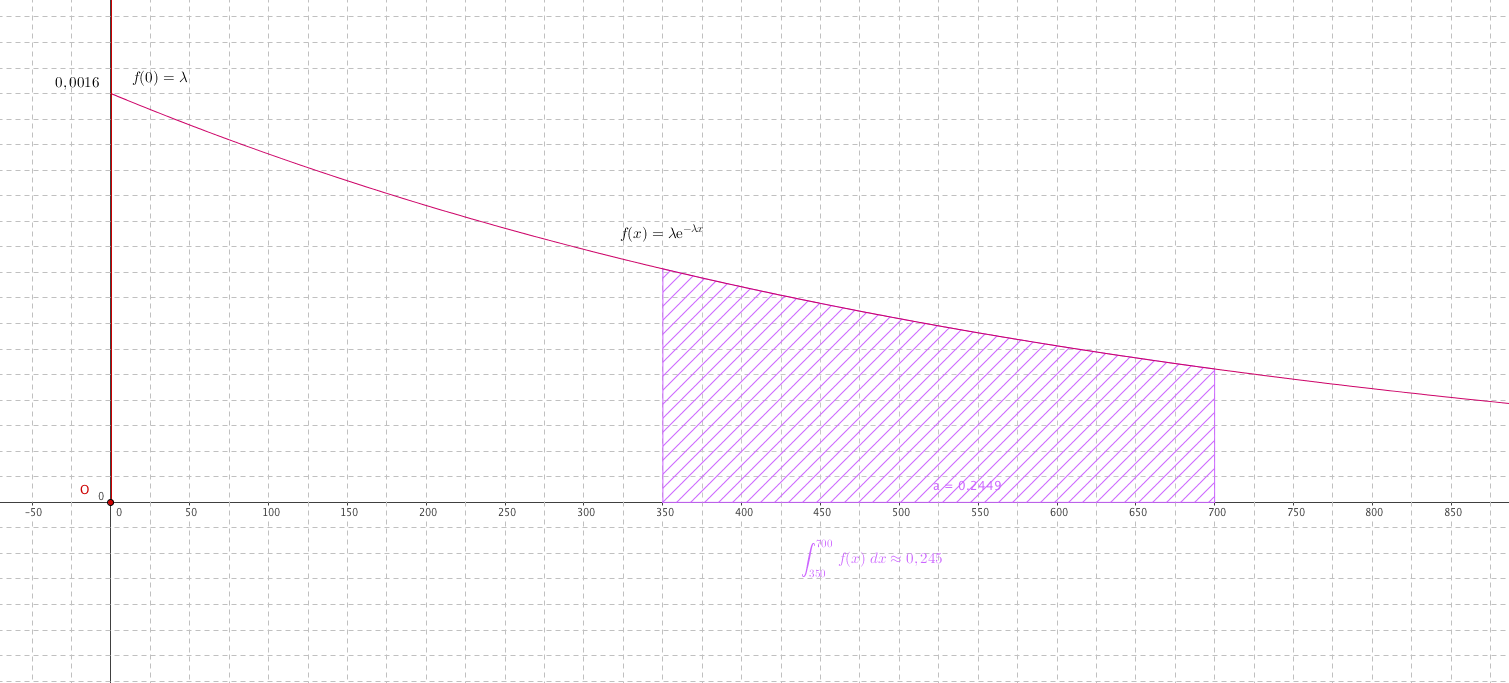
- Le graphique en ANNEXE 1 représente la fonction de densité de la loi exponentielle de paramètre $\lambda = 0,0016 $ $\left(\text{exprimé en jour}^{-1}\right)$.
- Représenter sur ce graphique la probabilité que $X$ soit comprise entre 350 jours et 700 jours.
- Calculer la probabilité que $X$ soit comprise entre $350$ jours et $700$ jours. Arrondir le résultat à $10^{-3}$. \begin{align*} P(350\leq X\leq 700) &=\displaystyle\int_{350}^{700} f(x)\; dx \\ &= \displaystyle\int_{350}^{700} \lambda \text{e}^{-\lambda x}\; dx \\ &=\left [ -\text{e}^{-\lambda x}\right ]_{350}^{700}\\ &= -\text{e}^{-700 \lambda }-\left (-\text{e}^{-350 \lambda }\right )\\ &=\text{e}^{-350 \times 0,0016 }-\text{e}^{-700 \times 0,0016 }\\ &\approx 0,245\\ \end{align*}
- Calculer la probabilité que $X$ soit de moins de $550$ jours. Arrondir à $10^{-3}$. \begin{align*} P( X\leq 550) &=\displaystyle\int_{0}^{550} f(x)\; dx \\ &= \displaystyle\int_{0}^{550} \lambda \text{e}^{-\lambda x}\; dx \\ &=\left [ -\text{e}^{-\lambda x}\right ]_{0}^{550}\\ &= -\text{e}^{-550 \lambda }-\left (-\text{e}^{0 }\right )\\ &=1-\text{e}^{-550 \times 0,0016 }\\ &\approx 0,5855\\ \end{align*}
- Déterminer la valeur de $x$ pour que $P(X < x) = 0,8$. Le résultat sera arrondi à l' unité. Interpréter ce résultat en le resituant dans le contexte . On cherche $x$ tel que $P(X < x) = 0,8$
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique ne sont pas sont réunies !
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
On obtient $I_{60}\approx [ 0; 0,0896]$
Partie B : les billes
Nos amis se demandent s'ils ne devraient pas plutôt commander des billes pour réparer les roulements évoqués dans la partie A. Ils commandent une grande quantité de billes de 6 mm de diamètre. Malheureusement, certaines présentent un défaut de diamètre. Ils s'aperçoivent qu'ils ne peuvent utiliser que les billes mesurant entre $5,9$ mm et $6,1$ mm. Sur la note du fabricant est indiqué que la variable aléatoire $D$ qui, à chaque bille, lui associe son diamètre, suit la loi normale d'espérance $\mu = 6$ mm et d'écart-type $\sigma = 0,05$ mm.
Partie C : les chaînes de vélo
Un tableau est mis à disposition pour permettre aux utilisateurs de savoir quand ils doivent changer leur chaîne de vélo. Par exemple, pour une personne utilisant son vélo en ville $\left(\text{vitesse moyenne } 16~ \text{km.h}^{-1}\right)$ environ 2 heures par jour, la durée de vie moyenne de la chaîne est de 625 jours. On admet que la durée de vie en jour, d'une chaîne de vélo pour un tel utilisateur est une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda$. On rappelle que la probabilité que $X$ soit inférieure ou égale à $t$ (exprimé en jour) vaut : $P(X \leqslant t) = 1 - \text{e}^{- \lambda t}$.
On sait que $P(X < x) = 1-\text{e}^{-\lambda x}$ \begin{align*} P( X\leq x) =0,8&\iff 1-\text{e}^{-\lambda x} =0,8 \\ &\iff \text{e}^{-\lambda x} =0,8 \\ &\iff -\lambda x =\ln(0,2) \\ &\iff x=-\dfrac{\ln(0,2)}{\lambda}\\ &\iff x=-\dfrac{\ln(0,2)}{0,0016}\\ &x\approx 1006\\ \end{align*} Il y a 80% de chance que la durée de vie moyenne de la chaîne soit inférieure à 1006 jours.
- Vues: 20777
