Baccalauréat STI 2D/STL spécialité SPCL Antilles-Guyane 19 juin 2014 - Correction de l'Exercice 4
Page 9 sur 9
Exercice 4 6 points
On note $f$ la fonction définie sur l'intervalle $]0~;~+ \infty[$ par \[f(x) = (2 - \ln x) \ln x.\] Sa courbe représentative $\mathcal{C}_{f}$ dans un repère orthonormal est donnée sur la feuille ANNEXE .
- Lire sur le graphique la limite de la fonction f en O. Retrouver ce résultat à l'aide de l'expression de f(x).
- Montrer que la fonction dérivée de f sur l'intervalle $]0~;~+ \infty[$ est définie par $f'(x) = \dfrac{2(1 - \ln x)}{x}$.
- Étudier le signe de $f'(x)$ lorsque $x$ est dans l'intervalle $]0~;~+ \infty[$ puis donner les variations de la fonction $f$ sur l'intervalle $]0~;~+ \infty[$.
-
- On appelle A et B les points d'intersection de la courbe $\mathcal{C}_{f}$ avec l'axe des abscisses (Voir le graphique). Calculer les abscisses des points A et B.
- Calculer le coefficient directeur de la tangente $\mathcal{T}$ à la courbe $\mathcal{C}_{f}$ au point A. Tracer la droite $\mathcal{T}$ sur le graphique donné en annexe.
Les abscisses des points A et B sont les réels $x$ strictement positifs, solutions de l'équation $f(x)=0$. Soit les réels $x$ strictement positifs tels que : $$\begin{array}{lll} \\ f(x) = 0 & \iff (2 - \ln x) \ln x = 0 \\ & \iff -\ln x > (2 - \ln x) = 0 \text{ ou } \ln x =0\\ & \iff \ln x =2 \text{ ou } \ln x =0 \\ & \iff x =e^2 \text{ ou } x =e^0 \\ & \iff x =e^2 \text{ ou } x =1 \\ \end{array}$$Les coordonnées des points A et B sont : A$ (1, 0)$ et B$(e^2;0)$.
Le coefficient directeur de la tangente $\mathcal{T}$ à la courbe $\mathcal{C}_{f}$ au point A d'abscisse 1 est $f'(1)=2$. - Montrer que la fonction $F$ définie par \[F(x) = - x(\ln x)^2 + 4x \ln x - 4x\] est une primitive de la fonction $f$ sur l'intervalle $]0~;~+ \infty[$.
- On note $\mathcal{D}$ le domaine du plan limité par la courbe $\mathcal{C}_{f}$, l'axe des abscisses et les droites d'équations respectives $x = 1$ et $x = \text{e}^2$.
- Hachurer sur le graphique donné en annexe le domaine $\mathcal{D}$.
- Calculer l'aire du domaine $\mathcal{D}$.
$\mathcal{D}$ est le domaine sous la courbe $\mathcal{C}_{f}$ colorié.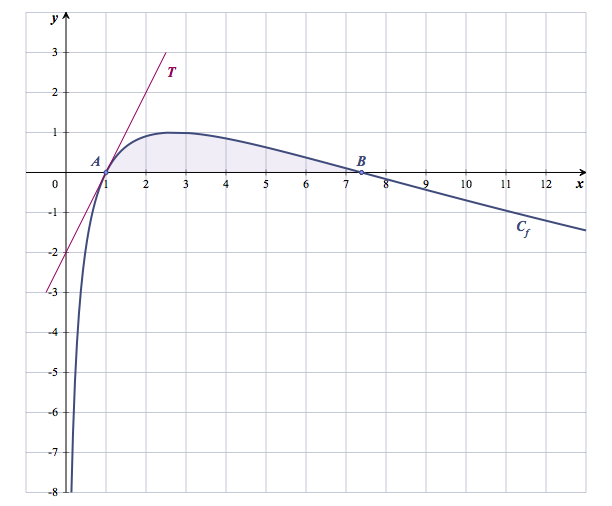
$$\begin{array}{ll} \mathcal{A}&= \displaystyle\int_{1}^{ \text{e}^2}f(x)\:\text{d}x&\\ & = \left [ F(x)\right ]_{1}^{ \text{e}^2} &\\ & = \left [ - x(\ln x)^2 + 4x \ln x - 4x\right ]_{1}^{ \text{e}^2} &\\ & = - \text{e}^2\left (\ln \left(\text{e}^2\right)\right )^2 + 4\text{e}^2 \ln \left (\text{e}^2\right ) - 4 \text{e}^2 -(-4)& \text{Or } \ln \left (\text{e}^2\right )=2 \ln \text{e} =2 \\ & =-4 &\\ \end{array}$$L'aire du domaine $\mathcal{D}$ est égale à 4 unités d'aire.
Graphiquement, il semblerait que la courbe $\mathcal{C}_{f}$ admette pour asymptote l'axe des ordonnées. On en déduit, par lecture graphique, que la limite de la fonction $f$ en 0 est $-\infty$
$\left.\begin{array}{l} \lim\limits_{x \to 0^+}~\ln x=-\infty\\ \lim\limits_{x \to 0^+}~2 - \ln x=+\infty \end{array}\right\}$ par produit on obtient: $\lim\limits_{x \to 0 ^+} (2 - \ln x) \ln x = -\infty$
$$\lim\limits_{x \to 0 ^+} f(x) = -\infty$$
$f$ est dérivable comme produit de deux fonctions dérivables : $f=uv$ d'où $f'=u' v+uv' $ avec pour tout réel $x$, dans $D_{ f}$ :
$\left\{ \begin{array}{l} u(x)~ =\ln x \\ v(x)~ =2 - \ln x \end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ =\dfrac{1}{x} \\ v'(x)~ =-\dfrac{1}{x} \end{array}\right.$
Soit pour tout réel $x$ strictement positif, $f$ est dérivable comme produit de deux fonctions dérivables : $f=uv$ d'où $f'=u' v+uv' $ avec pour tout réel $x$, dans $D_{ f}$ :
$\left\{ \begin{array}{l} u(x)~ =\ln x \\ v(x)~ =2 - \ln x \end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ =\dfrac{1}{x} \\ v'(x)~ =-\dfrac{1}{x} \end{array}\right.$
Ainsi pour tout réel $x$, dans $]0~;~+ \infty[$ : $$\begin{array}{ll} f'(x) &= \dfrac{1}{x}\times \left (2 - \ln x\right ) +\left (-\dfrac{1}{x}\right ) \times \ln x \\ & = \dfrac{ 2-\ln x - \ln x}{x} \\ & = \dfrac{ 2-2 \ln x }{x} \\ & = \dfrac{ 2\left ( 1 - \ln x \right ) }{x} \\ \end{array}$$
La dérivée de la fonction $f $ est la fonction $f'$ définie sur l'intervalle $]0~;~+ \infty[$ par $f'(x)= \dfrac{ 2\left ( 1 - \ln x \right ) }{x}$
Sur l'intervalle $]0~;~+ \infty[$, $f'(x)$ est du même signe que $1-\ln x $ et, pour tout réel $x$ strictement positif,
$$\begin{array}{lll} \\ f'(x) > 0 & \iff 1-\ln x > 0 & \\ & \iff -\ln x > -1 & \text{ en ajoutant } -1\\ & \iff \ln x < 1 & \text{ en multipliant par } -1 < 0 \\ & \iff e^{ \ln x } < e^1 & \text{ en appliquant la fonction exponentielle } \\ & \iff 0 < x < e & \text{ strictement croissante sur } ]0~;~+ \infty[\\ \end{array}$$
Les variations de la fonction $f$ se déduisent du signe de sa dérivée :
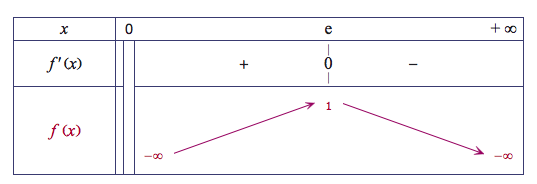
$f(e)= \left (2-\ln(e )\right )\ln e=1 $
$\left.\begin{array}{l} \lim\limits_{x \to +\infty}~ \ln x=+\infty \\ \lim\limits_{x \to +\infty}~2- \ln x=-\infty \end{array}\right\}$ par produit on obtient:
$\lim\limits_{x \to +\infty}f(x)=-\infty$
Pour tout réel $x$ strictement positif, $F(x) =x\left ( (-\ln x)^2 + 4 \ln x - 4\right )$.
$F$ est dérivable comme produit de deux fonctions dérivables : $f=uv$ d'où $f'=u' v+uv' $ avec pour tout réel $x$, dans $]0~;~+ \infty[$ :
$\left\{ \begin{array}{l} u(x)~ =x \\ v(x)~ =(-\ln x)^2 + 4 \ln x - 4 \end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ =1 \\ v'(x)~ =-2 \times \dfrac{1}{x} \times \ln x+ \dfrac{4}{x} =\dfrac{4 - 2 \ln x}{x}\end{array}\right.$
pour tout réel $x$, dans $]0~;~+ \infty[$ :
$\begin{array}{ll} F'(x) &= 1\times \left (-(\ln x)^2 + 4 \ln x - 4\right ) +\dfrac{4 - 2 \ln x}{x} \times x \\ & = -(\ln x)^2 + 4 \ln x - 4 +4 - 2 \ln x \\ & = -(\ln x)^2 + 2 \ln x \\ & = (2 - \ln x) \ln x \\ \end{array}$
Pour tout réel $x$ strictement positif, $F′(x)=f(x)$ donc la fonction $F$ définie par $F(x) = - x(\ln x)^2 + 4x \ln x - 4x$ est une primitive de la fonction $f$ sur l'intervalle $]0~;~+ \infty[$.
- Vues: 18447
